DiAMoNDBack: Diffusion-denoising Autoregressive Model for Non-Deterministic Backmapping of Cα Protein Traces

Coarse-grained molecular models of proteins permit access to length and time scales unattainable by all-atom models and the simulation of processes that occur on long-time scales such as aggregation and folding. The reduced resolution realizes computational accelerations but an atomistic representation can be vital for a complete understanding of mechanistic details. Backmapping is the process of restoring all-atom resolution to coarse-grained molecular models. In this work, we report DiAMoNDBack (Diffusion-denoising Autoregressive Model for Non-Deterministic Backmapping) as an autoregressive denoising diffusion probability model to restore all-atom details to coarse-grained protein representations retaining only C{\alpha} coordinates. The autoregressive generation process proceeds from the protein N-terminus to C-terminus in a residue-by-residue fashion conditioned on the C{\alpha} trace and previously backmapped backbone and side chain atoms within the local neighborhood. The local and autoregressive nature of our model makes it transferable between proteins. The stochastic nature of the denoising diffusion process means that the model generates a realistic ensemble of backbone and side chain all-atom configurations consistent with the coarse-grained C{\alpha} trace. We train DiAMoNDBack over 65k+ structures from Protein Data Bank (PDB) and validate it in applications to a hold-out PDB test set, intrinsically-disordered protein structures from the Protein Ensemble Database (PED), molecular dynamics simulations of fast-folding mini-proteins from DE Shaw Research, and coarse-grained simulation data. We achieve state-of-the-art reconstruction performance in terms of correct bond formation, avoidance of side chain clashes, and diversity of the generated side chain configurational states. We make DiAMoNDBack model publicly available as a free and open source Python package.

GANs and Closures: Micro-Macro Consistency in Multiscale Modeling

Sampling the phase space of molecular systems -- and, more generally, of complex systems effectively modeled by stochastic differential equations -- is a crucial modeling step in many fields, from protein folding to materials discovery. These problems are often multiscale in nature: they can be described in terms of low-dimensional effective free energy surfaces parametrized by a small number of "slow" reaction coordinates; the remaining "fast" degrees of freedom populate an equilibrium measure on the reaction coordinate values. Sampling procedures for such problems are used to estimate effective free energy differences as well as ensemble averages with respect to the conditional equilibrium distributions; these latter averages lead to closures for effective reduced dynamic models. Over the years, enhanced sampling techniques coupled with molecular simulation have been developed. An intriguing analogy arises with the field of Machine Learning (ML), where Generative Adversarial Networks can produce high dimensional samples from low dimensional probability distributions. This sample generation returns plausible high dimensional space realizations of a model state, from information about its low-dimensional representation. In this work, we present an approach that couples physics-based simulations and biasing methods for sampling conditional distributions with ML-based conditional generative adversarial networks for the same task. The "coarse descriptors" on which we condition the fine scale realizations can either be known a priori, or learned through nonlinear dimensionality reduction. We suggest that this may bring out the best features of both approaches: we demonstrate that a framework that couples cGANs with physics-based enhanced sampling techniques can improve multiscale SDE dynamical systems sampling, and even shows promise for systems of increasing complexity.

Molecular Latent Space Simulators

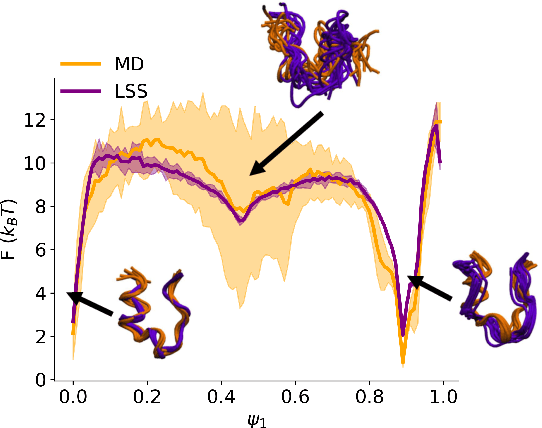
Small integration time steps limit molecular dynamics (MD) simulations to millisecond time scales. Markov state models (MSMs) and equation-free approaches learn low-dimensional kinetic models from MD simulation data by performing configurational or dynamical coarse-graining of the state space. The learned kinetic models enable the efficient generation of dynamical trajectories over vastly longer time scales than are accessible by MD, but the discretization of configurational space and/or absence of a means to reconstruct molecular configurations precludes the generation of continuous all-atom molecular trajectories. We propose latent space simulators (LSS) to learn kinetic models for continuous all-atom simulation trajectories by training three deep learning networks to (i) learn the slow collective variables of the molecular system, (ii) propagate the system dynamics within this slow latent space, and (iii) generatively reconstruct molecular configurations. We demonstrate the approach in an application to Trp-cage miniprotein to produce novel ultra-long synthetic folding trajectories that accurately reproduce all-atom molecular structure, thermodynamics, and kinetics at six orders of magnitude lower cost than MD. The dramatically lower cost of trajectory generation enables greatly improved sampling and greatly reduced statistical uncertainties in estimated thermodynamic averages and kinetic rates.

Discovery of Self-Assembling $π$-Conjugated Peptides by Active Learning-Directed Coarse-Grained Molecular Simulation

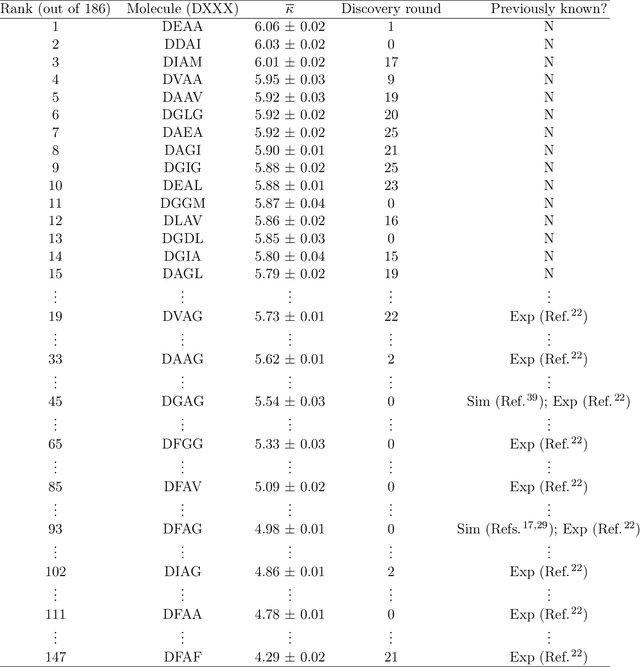
Electronically-active organic molecules have demonstrated great promise as novel soft materials for energy harvesting and transport. Self-assembled nanoaggregates formed from $\pi$-conjugated oligopeptides composed of an aromatic core flanked by oligopeptide wings offer emergent optoelectronic properties within a water soluble and biocompatible substrate. Nanoaggregate properties can be controlled by tuning core chemistry and peptide composition, but the sequence-structure-function relations remain poorly characterized. In this work, we employ coarse-grained molecular dynamics simulations within an active learning protocol employing deep representational learning and Bayesian optimization to efficiently identify molecules capable of assembling pseudo-1D nanoaggregates with good stacking of the electronically-active $\pi$-cores. We consider the DXXX-OPV3-XXXD oligopeptide family, where D is an Asp residue and OPV3 is an oligophenylene vinylene oligomer (1,4-distyrylbenzene), to identify the top performing XXX tripeptides within all 20$^3$ = 8,000 possible sequences. By direct simulation of only 2.3% of this space, we identify molecules predicted to exhibit superior assembly relative to those reported in prior work. Spectral clustering of the top candidates reveals new design rules governing assembly. This work establishes new understanding of DXXX-OPV3-XXXD assembly, identifies promising new candidates for experimental testing, and presents a computational design platform that can be generically extended to other peptide-based and peptide-like systems.

High-resolution Markov state models for the dynamics of Trp-cage miniprotein constructed over slow folding modes identified by state-free reversible VAMPnets

State-free reversible VAMPnets (SRVs) are a neural network-based framework capable of learning the leading eigenfunctions of the transfer operator of a dynamical system from trajectory data. In molecular dynamics simulations, these data-driven collective variables (CVs) capture the slowest modes of the dynamics and are useful for enhanced sampling and free energy estimation. In this work, we employ SRV coordinates as a feature set for Markov state model (MSM) construction. Compared to the current state of the art, MSMs constructed from SRV coordinates are more robust to the choice of input features, exhibit faster implied timescale convergence, and permit the use of shorter lagtimes to construct higher kinetic resolution models. We apply this methodology to study the folding kinetics and conformational landscape of the Trp-cage miniprotein. Folding and unfolding mean first passage times are in good agreement with prior literature, and a nine macrostate model is presented. The unfolded ensemble comprises a central kinetic hub with interconversions to several metastable unfolded conformations and which serves as the gateway to the folded ensemble. The folded ensemble comprises the native state, a partially unfolded intermediate "loop" state, and a previously unreported short-lived intermediate that we were able to resolve due to the high time-resolution of the SRV-MSM. We propose SRVs as an excellent candidate for integration into modern MSM construction pipelines.

Capabilities and Limitations of Time-lagged Autoencoders for Slow Mode Discovery in Dynamical Systems

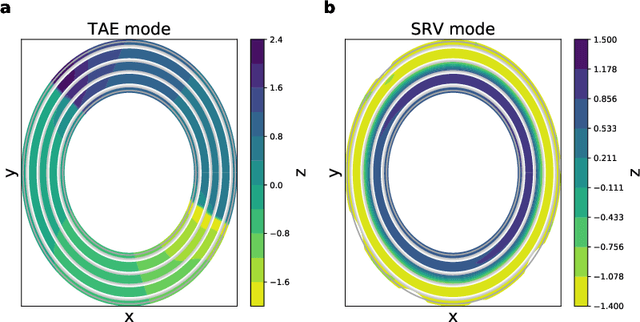
Time-lagged autoencoders (TAEs) have been proposed as a deep learning regression-based approach to the discovery of slow modes in dynamical systems. However, a rigorous analysis of nonlinear TAEs remains lacking. In this work, we discuss the capabilities and limitations of TAEs through both theoretical and numerical analyses. Theoretically, we derive bounds for nonlinear TAE performance in slow mode discovery and show that in general TAEs learn a mixture of slow and maximum variance modes. Numerically, we illustrate cases where TAEs can and cannot correctly identify the leading slowest mode in two example systems: a 2D "Washington beltway" potential and the alanine dipeptide molecule in explicit water. We also compare the TAE results with those obtained using state-free reversible VAMPnets (SRVs) as a variational-based neural network approach for slow modes discovery, and show that SRVs can correctly discover slow modes where TAEs fail.

Landmark Diffusion Maps (L-dMaps): Accelerated manifold learning out-of-sample extension

Diffusion maps are a nonlinear manifold learning technique based on harmonic analysis of a diffusion process over the data. Out-of-sample extensions with computational complexity $\mathcal{O}(N)$, where $N$ is the number of points comprising the manifold, frustrate applications to online learning applications requiring rapid embedding of high-dimensional data streams. We propose landmark diffusion maps (L-dMaps) to reduce the complexity to $\mathcal{O}(M)$, where $M \ll N$ is the number of landmark points selected using pruned spanning trees or k-medoids. Offering $(N/M)$ speedups in out-of-sample extension, L-dMaps enables the application of diffusion maps to high-volume and/or high-velocity streaming data. We illustrate our approach on three datasets: the Swiss roll, molecular simulations of a C$_{24}$H$_{50}$ polymer chain, and biomolecular simulations of alanine dipeptide. We demonstrate up to 50-fold speedups in out-of-sample extension for the molecular systems with less than 4% errors in manifold reconstruction fidelity relative to calculations over the full dataset.