Molecular Latent Space Simulators

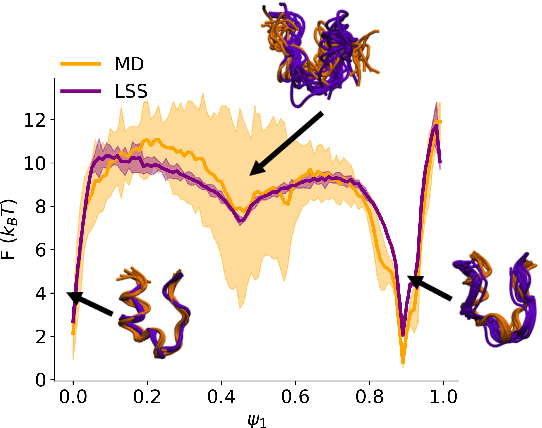
Small integration time steps limit molecular dynamics (MD) simulations to millisecond time scales. Markov state models (MSMs) and equation-free approaches learn low-dimensional kinetic models from MD simulation data by performing configurational or dynamical coarse-graining of the state space. The learned kinetic models enable the efficient generation of dynamical trajectories over vastly longer time scales than are accessible by MD, but the discretization of configurational space and/or absence of a means to reconstruct molecular configurations precludes the generation of continuous all-atom molecular trajectories. We propose latent space simulators (LSS) to learn kinetic models for continuous all-atom simulation trajectories by training three deep learning networks to (i) learn the slow collective variables of the molecular system, (ii) propagate the system dynamics within this slow latent space, and (iii) generatively reconstruct molecular configurations. We demonstrate the approach in an application to Trp-cage miniprotein to produce novel ultra-long synthetic folding trajectories that accurately reproduce all-atom molecular structure, thermodynamics, and kinetics at six orders of magnitude lower cost than MD. The dramatically lower cost of trajectory generation enables greatly improved sampling and greatly reduced statistical uncertainties in estimated thermodynamic averages and kinetic rates.

Discovery of Self-Assembling $π$-Conjugated Peptides by Active Learning-Directed Coarse-Grained Molecular Simulation

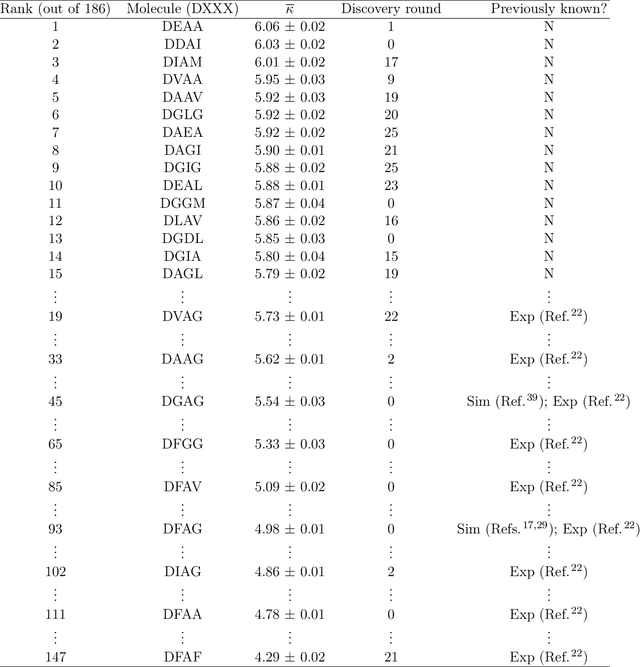
Electronically-active organic molecules have demonstrated great promise as novel soft materials for energy harvesting and transport. Self-assembled nanoaggregates formed from $\pi$-conjugated oligopeptides composed of an aromatic core flanked by oligopeptide wings offer emergent optoelectronic properties within a water soluble and biocompatible substrate. Nanoaggregate properties can be controlled by tuning core chemistry and peptide composition, but the sequence-structure-function relations remain poorly characterized. In this work, we employ coarse-grained molecular dynamics simulations within an active learning protocol employing deep representational learning and Bayesian optimization to efficiently identify molecules capable of assembling pseudo-1D nanoaggregates with good stacking of the electronically-active $\pi$-cores. We consider the DXXX-OPV3-XXXD oligopeptide family, where D is an Asp residue and OPV3 is an oligophenylene vinylene oligomer (1,4-distyrylbenzene), to identify the top performing XXX tripeptides within all 20$^3$ = 8,000 possible sequences. By direct simulation of only 2.3% of this space, we identify molecules predicted to exhibit superior assembly relative to those reported in prior work. Spectral clustering of the top candidates reveals new design rules governing assembly. This work establishes new understanding of DXXX-OPV3-XXXD assembly, identifies promising new candidates for experimental testing, and presents a computational design platform that can be generically extended to other peptide-based and peptide-like systems.

High-resolution Markov state models for the dynamics of Trp-cage miniprotein constructed over slow folding modes identified by state-free reversible VAMPnets

State-free reversible VAMPnets (SRVs) are a neural network-based framework capable of learning the leading eigenfunctions of the transfer operator of a dynamical system from trajectory data. In molecular dynamics simulations, these data-driven collective variables (CVs) capture the slowest modes of the dynamics and are useful for enhanced sampling and free energy estimation. In this work, we employ SRV coordinates as a feature set for Markov state model (MSM) construction. Compared to the current state of the art, MSMs constructed from SRV coordinates are more robust to the choice of input features, exhibit faster implied timescale convergence, and permit the use of shorter lagtimes to construct higher kinetic resolution models. We apply this methodology to study the folding kinetics and conformational landscape of the Trp-cage miniprotein. Folding and unfolding mean first passage times are in good agreement with prior literature, and a nine macrostate model is presented. The unfolded ensemble comprises a central kinetic hub with interconversions to several metastable unfolded conformations and which serves as the gateway to the folded ensemble. The folded ensemble comprises the native state, a partially unfolded intermediate "loop" state, and a previously unreported short-lived intermediate that we were able to resolve due to the high time-resolution of the SRV-MSM. We propose SRVs as an excellent candidate for integration into modern MSM construction pipelines.

Capabilities and Limitations of Time-lagged Autoencoders for Slow Mode Discovery in Dynamical Systems

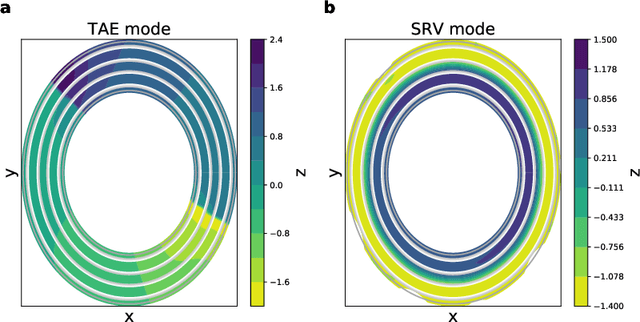
Time-lagged autoencoders (TAEs) have been proposed as a deep learning regression-based approach to the discovery of slow modes in dynamical systems. However, a rigorous analysis of nonlinear TAEs remains lacking. In this work, we discuss the capabilities and limitations of TAEs through both theoretical and numerical analyses. Theoretically, we derive bounds for nonlinear TAE performance in slow mode discovery and show that in general TAEs learn a mixture of slow and maximum variance modes. Numerically, we illustrate cases where TAEs can and cannot correctly identify the leading slowest mode in two example systems: a 2D "Washington beltway" potential and the alanine dipeptide molecule in explicit water. We also compare the TAE results with those obtained using state-free reversible VAMPnets (SRVs) as a variational-based neural network approach for slow modes discovery, and show that SRVs can correctly discover slow modes where TAEs fail.

Nonlinear Discovery of Slow Molecular Modes using Hierarchical Dynamics Encoders

The success of enhanced sampling molecular simulations that accelerate along collective variables (CVs) is predicated on the availability of variables coincident with the slow collective motions governing the long-time conformational dynamics of a system. It is challenging to intuit these slow CVs for all but the simplest molecular systems, and their data-driven discovery directly from molecular simulation trajectories has been a central focus of the molecular simulation community to both unveil the important physical mechanisms and to drive enhanced sampling. In this work, we introduce hierarchical dynamics encoder (HDE) as a deep learning architecture that learns nonlinear CV approximants to the leading slow eigenfunctions of the spectral decomposition of the transfer operator that evolves equilibrium-scaled probability distributions through time. Orthogonality of the learned CVs is naturally imposed within network training without added regularization. The CVs are inherently explicit and differentiable functions of the input coordinates making them well-suited to use in enhanced sampling calculations. We demonstrate the utility of HDEs in capturing parsimonious nonlinear representations of complex system dynamics in applications to 1D and 2D toy systems where the true eigenfunctions are exactly calculable and to molecular dynamics simulations of alanine dipeptide and the WW domain protein.