Aleksandr Andrejčuk
Applications of Koopman Mode Analysis to Neural Networks
Jun 21, 2020

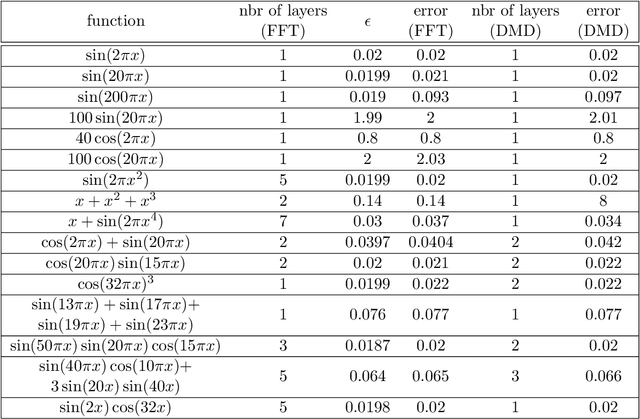
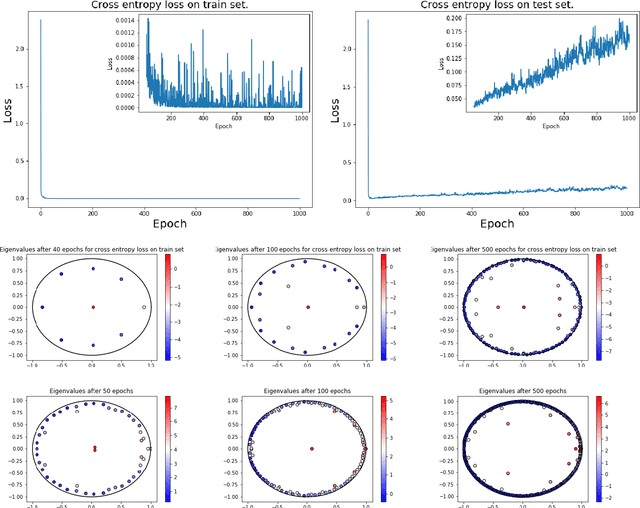
Abstract:We consider the training process of a neural network as a dynamical system acting on the high-dimensional weight space. Each epoch is an application of the map induced by the optimization algorithm and the loss function. Using this induced map, we can apply observables on the weight space and measure their evolution. The evolution of the observables are given by the Koopman operator associated with the induced dynamical system. We use the spectrum and modes of the Koopman operator to realize the above objectives. Our methods can help to, a priori, determine the network depth; determine if we have a bad initialization of the network weights, allowing a restart before training too long; speeding up the training time. Additionally, our methods help enable noise rejection and improve robustness. We show how the Koopman spectrum can be used to determine the number of layers required for the architecture. Additionally, we show how we can elucidate the convergence versus non-convergence of the training process by monitoring the spectrum, in particular, how the existence of eigenvalues clustering around 1 determines when to terminate the learning process. We also show how using Koopman modes we can selectively prune the network to speed up the training procedure. Finally, we show that incorporating loss functions based on negative Sobolev norms can allow for the reconstruction of a multi-scale signal polluted by very large amounts of noise.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge