Operator learning without the adjoint

There is a mystery at the heart of operator learning: how can one recover a non-self-adjoint operator from data without probing the adjoint? Current practical approaches suggest that one can accurately recover an operator while only using data generated by the forward action of the operator without access to the adjoint. However, naively, it seems essential to sample the action of the adjoint. In this paper, we partially explain this mystery by proving that without querying the adjoint, one can approximate a family of non-self-adjoint infinite-dimensional compact operators via projection onto a Fourier basis. We then apply the result to recovering Green's functions of elliptic partial differential operators and derive an adjoint-free sample complexity bound. While existing theory justifies low sample complexity in operator learning, ours is the first adjoint-free analysis that attempts to close the gap between theory and practice.

Elliptic PDE learning is provably data-efficient

PDE learning is an emerging field that combines physics and machine learning to recover unknown physical systems from experimental data. While deep learning models traditionally require copious amounts of training data, recent PDE learning techniques achieve spectacular results with limited data availability. Still, these results are empirical. Our work provides theoretical guarantees on the number of input-output training pairs required in PDE learning, explaining why these methods can be data-efficient. Specifically, we exploit randomized numerical linear algebra and PDE theory to derive a provably data-efficient algorithm that recovers solution operators of 3D elliptic PDEs from input-output data and achieves an exponential convergence rate with respect to the size of the training dataset with an exceptionally high probability of success.

Arbitrary-Depth Universal Approximation Theorems for Operator Neural Networks

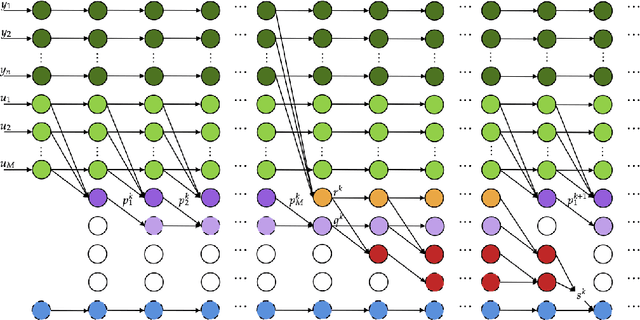
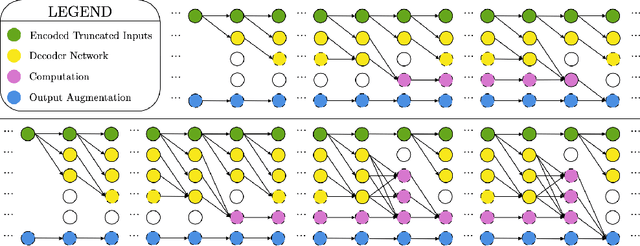
The standard Universal Approximation Theorem for operator neural networks (NNs) holds for arbitrary width and bounded depth. Here, we prove that operator NNs of bounded width and arbitrary depth are universal approximators for continuous nonlinear operators. In our main result, we prove that for non-polynomial activation functions that are continuously differentiable at a point with a nonzero derivative, one can construct an operator NN of width five, whose inputs are real numbers with finite decimal representations, that is arbitrarily close to any given continuous nonlinear operator. We derive an analogous result for non-affine polynomial activation functions. We also show that depth has theoretical advantages by constructing operator ReLU NNs of depth $2k^3+8$ and constant width that cannot be well-approximated by any operator ReLU NN of depth $k$, unless its width is exponential in $k$.