Structure-Preserving Operator Learning

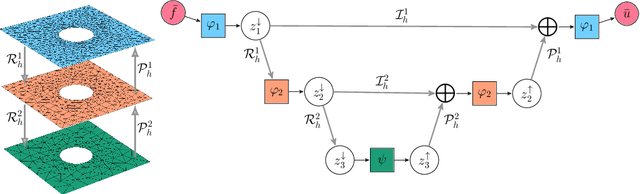
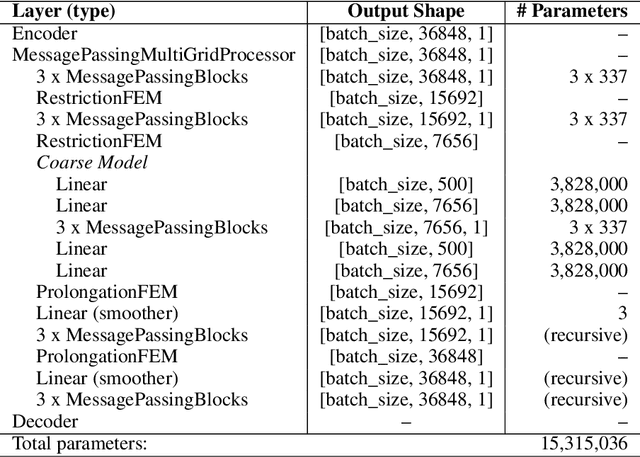
Learning complex dynamics driven by partial differential equations directly from data holds great promise for fast and accurate simulations of complex physical systems. In most cases, this problem can be formulated as an operator learning task, where one aims to learn the operator representing the physics of interest, which entails discretization of the continuous system. However, preserving key continuous properties at the discrete level, such as boundary conditions, and addressing physical systems with complex geometries is challenging for most existing approaches. We introduce a family of operator learning architectures, structure-preserving operator networks (SPONs), that allows to preserve key mathematical and physical properties of the continuous system by leveraging finite element (FE) discretizations of the input-output spaces. SPONs are encode-process-decode architectures that are end-to-end differentiable, where the encoder and decoder follows from the discretizations of the input-output spaces. SPONs can operate on complex geometries, enforce certain boundary conditions exactly, and offer theoretical guarantees. Our framework provides a flexible way of devising structure-preserving architectures tailored to specific applications, and offers an explicit trade-off between performance and efficiency, all thanks to the FE discretization of the input-output spaces. Additionally, we introduce a multigrid-inspired SPON architecture that yields improved performance at higher efficiency. Finally, we release a software to automate the design and training of SPON architectures.

Differentiable programming across the PDE and Machine Learning barrier

The combination of machine learning and physical laws has shown immense potential for solving scientific problems driven by partial differential equations (PDEs) with the promise of fast inference, zero-shot generalisation, and the ability to discover new physics. Examples include the use of fundamental physical laws as inductive bias to machine learning algorithms, also referred to as physics-driven machine learning, and the application of machine learning to represent features not represented in the differential equations such as closures for unresolved spatiotemporal scales. However, the simulation of complex physical systems by coupling advanced numerics for PDEs with state-of-the-art machine learning demands the composition of specialist PDE solving frameworks with industry-standard machine learning tools. Hand-rolling either the PDE solver or the neural net will not cut it. In this work, we introduce a generic differentiable programming abstraction that provides scientists and engineers with a highly productive way of specifying end-to-end differentiable models coupling machine learning and PDE-based components, while relying on code generation for high performance. Our interface automates the coupling of arbitrary PDE-based systems and machine learning models and unlocks new applications that could not hitherto be tackled, while only requiring trivial changes to existing code. Our framework has been adopted in the Firedrake finite-element library and supports the PyTorch and JAX ecosystems, as well as downstream libraries.

REXEL: An End-to-end Model for Document-Level Relation Extraction and Entity Linking

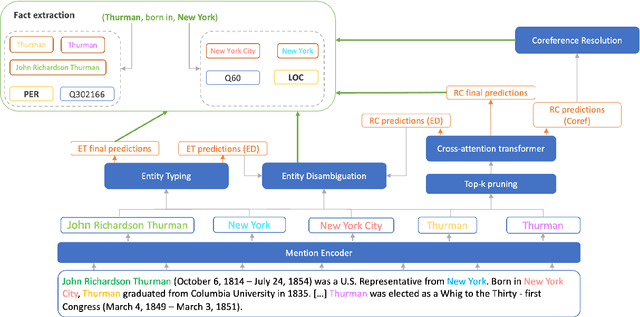
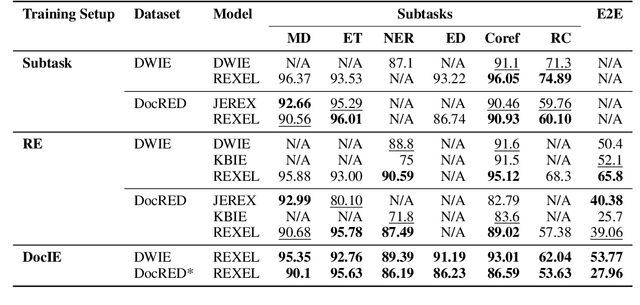
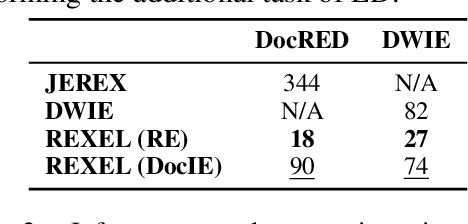
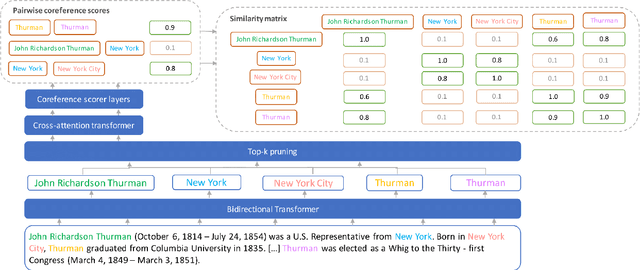
Extracting structured information from unstructured text is critical for many downstream NLP applications and is traditionally achieved by closed information extraction (cIE). However, existing approaches for cIE suffer from two limitations: (i) they are often pipelines which makes them prone to error propagation, and/or (ii) they are restricted to sentence level which prevents them from capturing long-range dependencies and results in expensive inference time. We address these limitations by proposing REXEL, a highly efficient and accurate model for the joint task of document level cIE (DocIE). REXEL performs mention detection, entity typing, entity disambiguation, coreference resolution and document-level relation classification in a single forward pass to yield facts fully linked to a reference knowledge graph. It is on average 11 times faster than competitive existing approaches in a similar setting and performs competitively both when optimised for any of the individual subtasks and a variety of combinations of different joint tasks, surpassing the baselines by an average of more than 6 F1 points. The combination of speed and accuracy makes REXEL an accurate cost-efficient system for extracting structured information at web-scale. We also release an extension of the DocRED dataset to enable benchmarking of future work on DocIE, which is available at https://github.com/amazon-science/e2e-docie.

Physics-driven machine learning models coupling PyTorch and Firedrake

Partial differential equations (PDEs) are central to describing and modelling complex physical systems that arise in many disciplines across science and engineering. However, in many realistic applications PDE modelling provides an incomplete description of the physics of interest. PDE-based machine learning techniques are designed to address this limitation. In this approach, the PDE is used as an inductive bias enabling the coupled model to rely on fundamental physical laws while requiring less training data. The deployment of high-performance simulations coupling PDEs and machine learning to complex problems necessitates the composition of capabilities provided by machine learning and PDE-based frameworks. We present a simple yet effective coupling between the machine learning framework PyTorch and the PDE system Firedrake that provides researchers, engineers and domain specialists with a high productive way of specifying coupled models while only requiring trivial changes to existing code.

Optimal Order Simple Regret for Gaussian Process Bandits

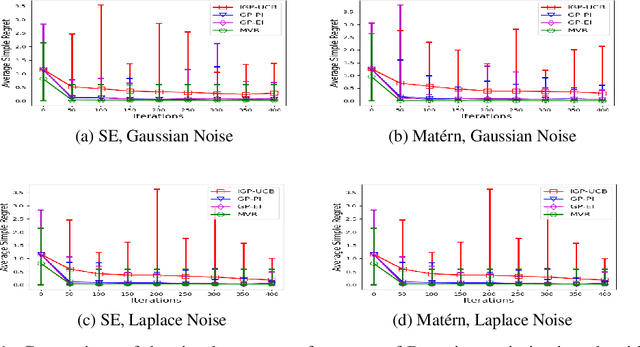
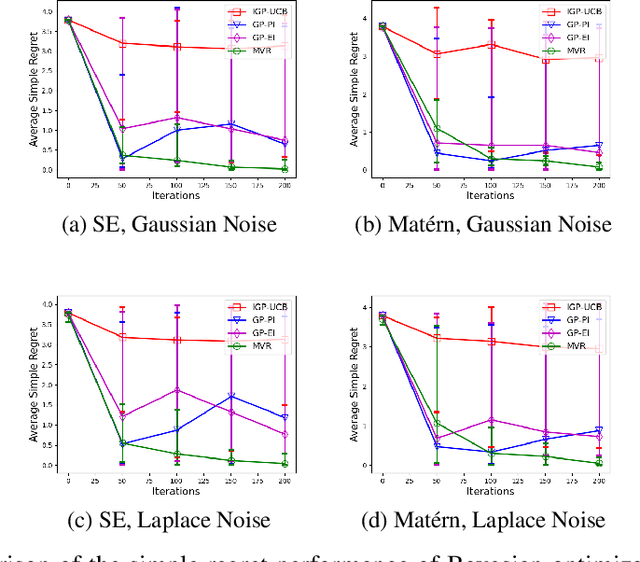
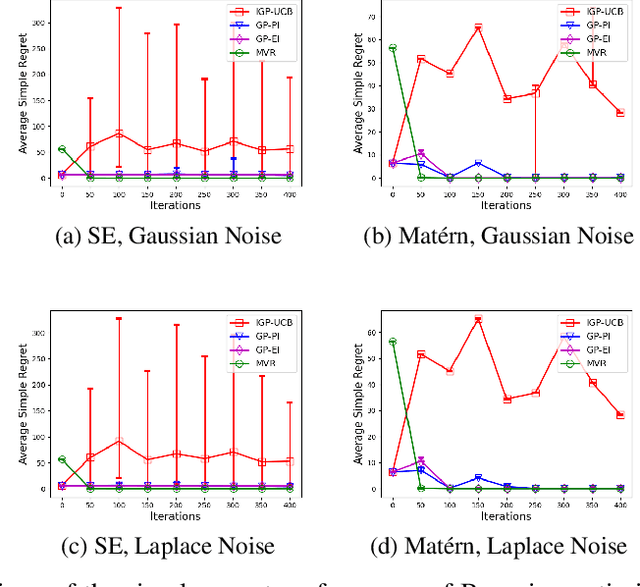
Consider the sequential optimization of a continuous, possibly non-convex, and expensive to evaluate objective function $f$. The problem can be cast as a Gaussian Process (GP) bandit where $f$ lives in a reproducing kernel Hilbert space (RKHS). The state of the art analysis of several learning algorithms shows a significant gap between the lower and upper bounds on the simple regret performance. When $N$ is the number of exploration trials and $\gamma_N$ is the maximal information gain, we prove an $\tilde{\mathcal{O}}(\sqrt{\gamma_N/N})$ bound on the simple regret performance of a pure exploration algorithm that is significantly tighter than the existing bounds. We show that this bound is order optimal up to logarithmic factors for the cases where a lower bound on regret is known. To establish these results, we prove novel and sharp confidence intervals for GP models applicable to RKHS elements which may be of broader interest.