Density estimation with LLMs: a geometric investigation of in-context learning trajectories

Large language models (LLMs) demonstrate remarkable emergent abilities to perform in-context learning across various tasks, including time series forecasting. This work investigates LLMs' ability to estimate probability density functions (PDFs) from data observed in-context; such density estimation (DE) is a fundamental task underlying many probabilistic modeling problems. We leverage the Intensive Principal Component Analysis (InPCA) to visualize and analyze the in-context learning dynamics of LLaMA-2 models. Our main finding is that these LLMs all follow similar learning trajectories in a low-dimensional InPCA space, which are distinct from those of traditional density estimation methods like histograms and Gaussian kernel density estimation (KDE). We interpret the LLaMA in-context DE process as a KDE with an adaptive kernel width and shape. This custom kernel model captures a significant portion of LLaMA's behavior despite having only two parameters. We further speculate on why LLaMA's kernel width and shape differs from classical algorithms, providing insights into the mechanism of in-context probabilistic reasoning in LLMs.

Lines of Thought in Large Language Models

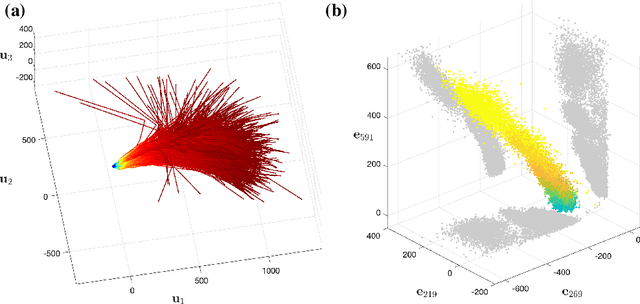
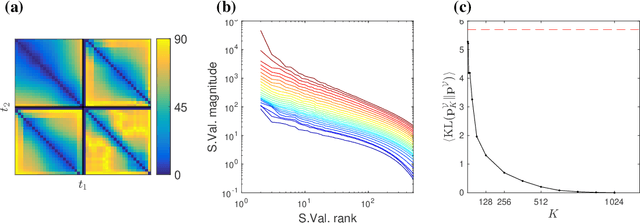
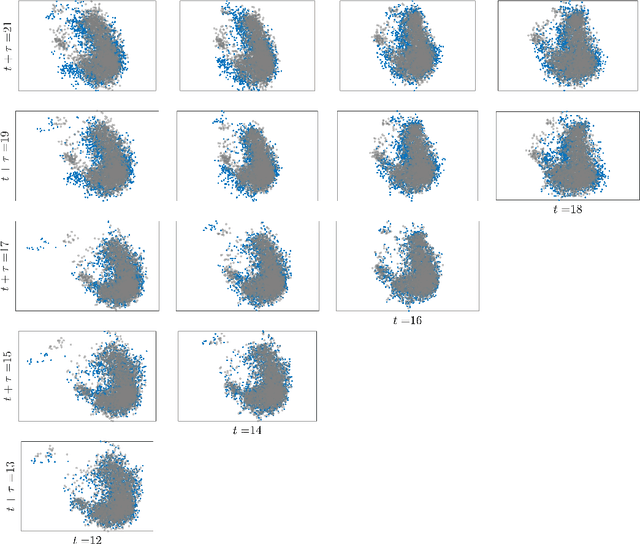
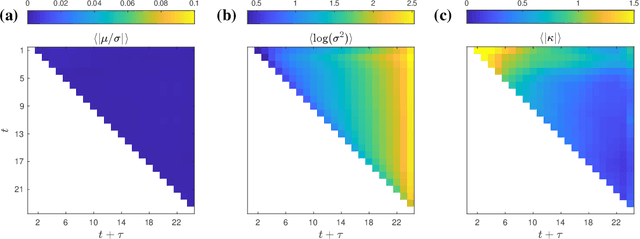
Large Language Models achieve next-token prediction by transporting a vectorized piece of text (prompt) across an accompanying embedding space under the action of successive transformer layers. The resulting high-dimensional trajectories realize different contextualization, or 'thinking', steps, and fully determine the output probability distribution. We aim to characterize the statistical properties of ensembles of these 'lines of thought.' We observe that independent trajectories cluster along a low-dimensional, non-Euclidean manifold, and that their path can be well approximated by a stochastic equation with few parameters extracted from data. We find it remarkable that the vast complexity of such large models can be reduced to a much simpler form, and we reflect on implications.

LLMs learn governing principles of dynamical systems, revealing an in-context neural scaling law

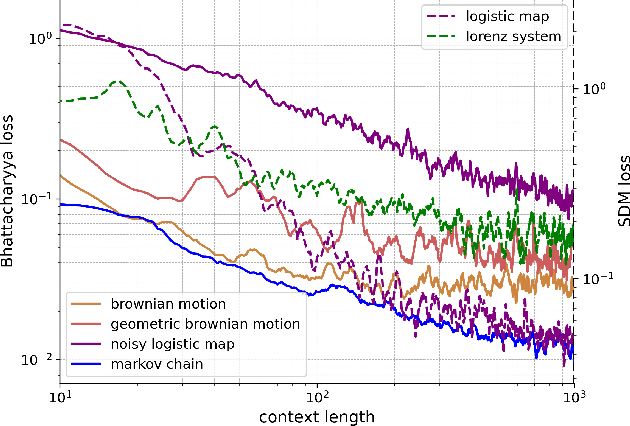
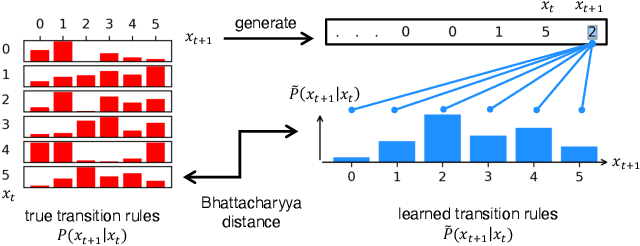
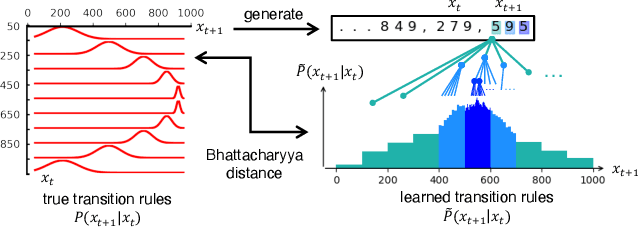
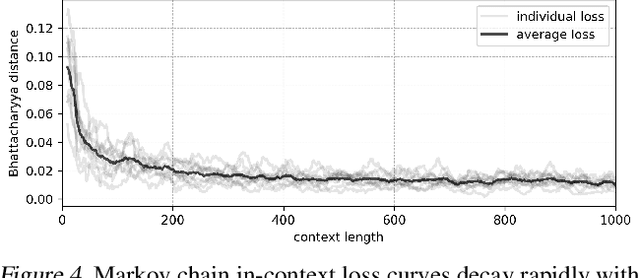
Pretrained large language models (LLMs) are surprisingly effective at performing zero-shot tasks, including time-series forecasting. However, understanding the mechanisms behind such capabilities remains highly challenging due to the complexity of the models. In this paper, we study LLMs' ability to extrapolate the behavior of dynamical systems whose evolution is governed by principles of physical interest. Our results show that LLaMA 2, a language model trained primarily on texts, achieves accurate predictions of dynamical system time series without fine-tuning or prompt engineering. Moreover, the accuracy of the learned physical rules increases with the length of the input context window, revealing an in-context version of neural scaling law. Along the way, we present a flexible and efficient algorithm for extracting probability density functions of multi-digit numbers directly from LLMs.

Coneheads: Hierarchy Aware Attention

Attention networks such as transformers have achieved state-of-the-art performance in many domains. These networks rely heavily on the dot product attention operator, which computes the similarity between two points by taking their inner product. However, the inner product does not explicitly model the complex structural properties of real world datasets, such as hierarchies between data points. To remedy this, we introduce cone attention, a drop-in replacement for dot product attention based on hyperbolic entailment cones. Cone attention associates two points by the depth of their lowest common ancestor in a hierarchy defined by hyperbolic cones, which intuitively measures the divergence of two points and gives a hierarchy aware similarity score. We test cone attention on a wide variety of models and tasks and show that it improves task-level performance over dot product attention and other baselines, and is able to match dot-product attention with significantly fewer parameters. Our results suggest that cone attention is an effective way to capture hierarchical relationships when calculating attention.

Shadow Cones: Unveiling Partial Orders in Hyperbolic Space

Hyperbolic space has been shown to produce superior low-dimensional embeddings of hierarchical structures that are unattainable in Euclidean space. Building upon this, the entailment cone formulation of Ganea et al. uses geodesically convex cones to embed partial orderings in hyperbolic space. However, these entailment cones lack intuitive interpretations due to their definitions via complex concepts such as tangent vectors and the exponential map in Riemannian space. In this paper, we present shadow cones, an innovative framework that provides a physically intuitive interpretation for defining partial orders on general manifolds. This is achieved through the use of metaphoric light sources and object shadows, inspired by the sun-earth-moon relationship. Shadow cones consist of two primary classes: umbral and penumbral cones. Our results indicate that shadow cones offer robust representation and generalization capabilities across a variety of datasets, such as WordNet and ConceptNet, thereby outperforming the top-performing entailment cones. Our findings indicate that shadow cones offer an innovative, general approach to geometrically encode partial orders, enabling better representation and analysis of datasets with hierarchical structures.