LLMs learn governing principles of dynamical systems, revealing an in-context neural scaling law
Paper and Code
Feb 01, 2024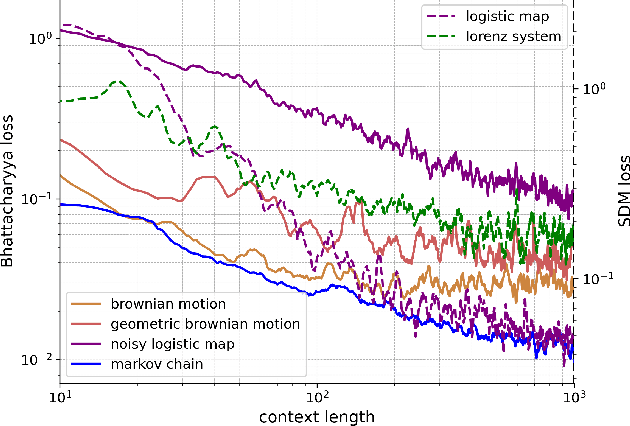
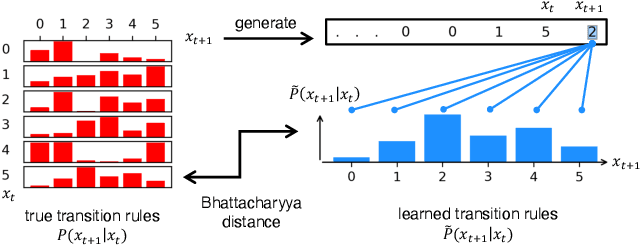
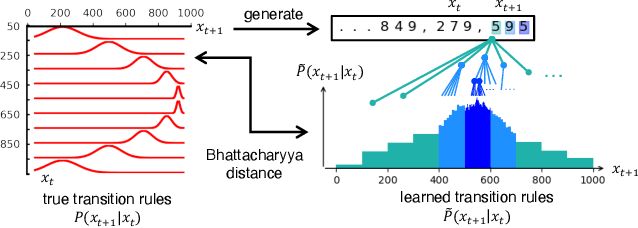
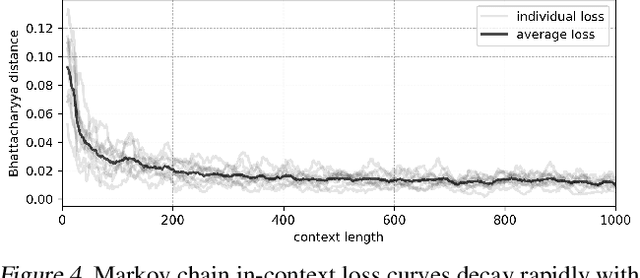
Pretrained large language models (LLMs) are surprisingly effective at performing zero-shot tasks, including time-series forecasting. However, understanding the mechanisms behind such capabilities remains highly challenging due to the complexity of the models. In this paper, we study LLMs' ability to extrapolate the behavior of dynamical systems whose evolution is governed by principles of physical interest. Our results show that LLaMA 2, a language model trained primarily on texts, achieves accurate predictions of dynamical system time series without fine-tuning or prompt engineering. Moreover, the accuracy of the learned physical rules increases with the length of the input context window, revealing an in-context version of neural scaling law. Along the way, we present a flexible and efficient algorithm for extracting probability density functions of multi-digit numbers directly from LLMs.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge