Deep Symmetric Autoencoders from the Eckart-Young-Schmidt Perspective

Deep autoencoders have become a fundamental tool in various machine learning applications, ranging from dimensionality reduction and reduced order modeling of partial differential equations to anomaly detection and neural machine translation. Despite their empirical success, a solid theoretical foundation for their expressiveness remains elusive, particularly when compared to classical projection-based techniques. In this work, we aim to take a step forward in this direction by presenting a comprehensive analysis of what we refer to as symmetric autoencoders, a broad class of deep learning architectures ubiquitous in the literature. Specifically, we introduce a formal distinction between different classes of symmetric architectures, analyzing their strengths and limitations from a mathematical perspective. For instance, we show that the reconstruction error of symmetric autoencoders with orthonormality constraints can be understood by leveraging the well-renowned Eckart-Young-Schmidt (EYS) theorem. As a byproduct of our analysis, we end up developing the EYS initialization strategy for symmetric autoencoders, which is based on an iterated application of the Singular Value Decomposition (SVD). To validate our findings, we conduct a series of numerical experiments where we benchmark our proposal against conventional deep autoencoders, discussing the importance of model design and initialization.

Handling geometrical variability in nonlinear reduced order modeling through Continuous Geometry-Aware DL-ROMs

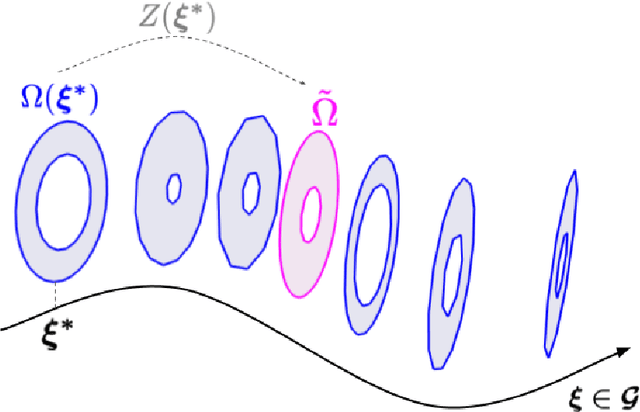
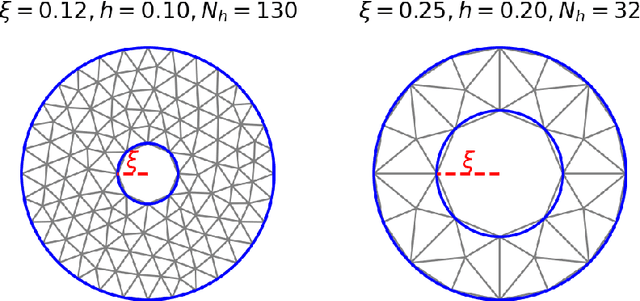
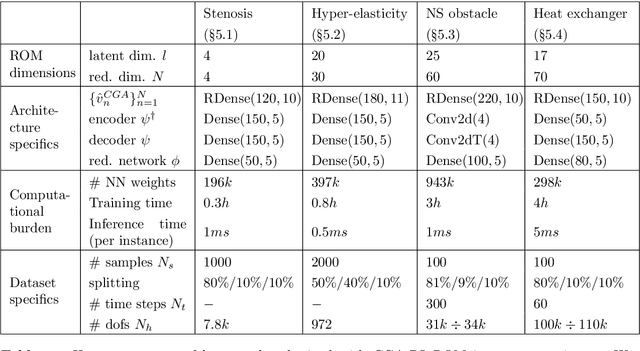
Deep Learning-based Reduced Order Models (DL-ROMs) provide nowadays a well-established class of accurate surrogate models for complex physical systems described by parametrized PDEs, by nonlinearly compressing the solution manifold into a handful of latent coordinates. Until now, design and application of DL-ROMs mainly focused on physically parameterized problems. Within this work, we provide a novel extension of these architectures to problems featuring geometrical variability and parametrized domains, namely, we propose Continuous Geometry-Aware DL-ROMs (CGA-DL-ROMs). In particular, the space-continuous nature of the proposed architecture matches the need to deal with multi-resolution datasets, which are quite common in the case of geometrically parametrized problems. Moreover, CGA-DL-ROMs are endowed with a strong inductive bias that makes them aware of geometrical parametrizations, thus enhancing both the compression capability and the overall performance of the architecture. Within this work, we justify our findings through a thorough theoretical analysis, and we practically validate our claims by means of a series of numerical tests encompassing physically-and-geometrically parametrized PDEs, ranging from the unsteady Navier-Stokes equations for fluid dynamics to advection-diffusion-reaction equations for mathematical biology.

On latent dynamics learning in nonlinear reduced order modeling

In this work, we present the novel mathematical framework of latent dynamics models (LDMs) for reduced order modeling of parameterized nonlinear time-dependent PDEs. Our framework casts this latter task as a nonlinear dimensionality reduction problem, while constraining the latent state to evolve accordingly to an (unknown) dynamical system. A time-continuous setting is employed to derive error and stability estimates for the LDM approximation of the full order model (FOM) solution. We analyze the impact of using an explicit Runge-Kutta scheme in the time-discrete setting, resulting in the $\Delta\text{LDM}$ formulation, and further explore the learnable setting, $\Delta\text{LDM}_\theta$, where deep neural networks approximate the discrete LDM components, while providing a bounded approximation error with respect to the FOM. Moreover, we extend the concept of parameterized Neural ODE - recently proposed as a possible way to build data-driven dynamical systems with varying input parameters - to be a convolutional architecture, where the input parameters information is injected by means of an affine modulation mechanism, while designing a convolutional autoencoder neural network able to retain spatial-coherence, thus enhancing interpretability at the latent level. Numerical experiments, including the Burgers' and the advection-reaction-diffusion equations, demonstrate the framework's ability to obtain, in a multi-query context, a time-continuous approximation of the FOM solution, thus being able to query the LDM approximation at any given time instance while retaining a prescribed level of accuracy. Our findings highlight the remarkable potential of the proposed LDMs, representing a mathematically rigorous framework to enhance the accuracy and approximation capabilities of reduced order modeling for time-dependent parameterized PDEs.

PTPI-DL-ROMs: pre-trained physics-informed deep learning-based reduced order models for nonlinear parametrized PDEs

The coupling of Proper Orthogonal Decomposition (POD) and deep learning-based ROMs (DL-ROMs) has proved to be a successful strategy to construct non-intrusive, highly accurate, surrogates for the real time solution of parametric nonlinear time-dependent PDEs. Inexpensive to evaluate, POD-DL-ROMs are also relatively fast to train, thanks to their limited complexity. However, POD-DL-ROMs account for the physical laws governing the problem at hand only through the training data, that are usually obtained through a full order model (FOM) relying on a high-fidelity discretization of the underlying equations. Moreover, the accuracy of POD-DL-ROMs strongly depends on the amount of available data. In this paper, we consider a major extension of POD-DL-ROMs by enforcing the fulfillment of the governing physical laws in the training process -- that is, by making them physics-informed -- to compensate for possible scarce and/or unavailable data and improve the overall reliability. To do that, we first complement POD-DL-ROMs with a trunk net architecture, endowing them with the ability to compute the problem's solution at every point in the spatial domain, and ultimately enabling a seamless computation of the physics-based loss by means of the strong continuous formulation. Then, we introduce an efficient training strategy that limits the notorious computational burden entailed by a physics-informed training phase. In particular, we take advantage of the few available data to develop a low-cost pre-training procedure; then, we fine-tune the architecture in order to further improve the prediction reliability. Accuracy and efficiency of the resulting pre-trained physics-informed DL-ROMs (PTPI-DL-ROMs) are then assessed on a set of test cases ranging from non-affinely parametrized advection-diffusion-reaction equations, to nonlinear problems like the Navier-Stokes equations for fluid flows.