Interpretable and Efficient Data-driven Discovery and Control of Distributed Systems

Effectively controlling systems governed by Partial Differential Equations (PDEs) is crucial in several fields of Applied Sciences and Engineering. These systems usually yield significant challenges to conventional control schemes due to their nonlinear dynamics, partial observability, high-dimensionality once discretized, distributed nature, and the requirement for low-latency feedback control. Reinforcement Learning (RL), particularly Deep RL (DRL), has recently emerged as a promising control paradigm for such systems, demonstrating exceptional capabilities in managing high-dimensional, nonlinear dynamics. However, DRL faces challenges including sample inefficiency, robustness issues, and an overall lack of interpretability. To address these issues, we propose a data-efficient, interpretable, and scalable Dyna-style Model-Based RL framework for PDE control, combining the Sparse Identification of Nonlinear Dynamics with Control (SINDy-C) algorithm and an autoencoder (AE) framework for the sake of dimensionality reduction of PDE states and actions. This novel approach enables fast rollouts, reducing the need for extensive environment interactions, and provides an interpretable latent space representation of the PDE forward dynamics. We validate our method on two PDE problems describing fluid flows - namely, the 1D Burgers equation and 2D Navier-Stokes equations - comparing it against a model-free baseline, and carrying out an extensive analysis of the learned dynamics.

Denoising Diffusion Planner: Learning Complex Paths from Low-Quality Demonstrations

Denoising Diffusion Probabilistic Models (DDPMs) are powerful generative deep learning models that have been very successful at image generation, and, very recently, in path planning and control. In this paper, we investigate how to leverage the generalization and conditional-sampling capabilities of DDPMs to generate complex paths for a robotic end effector. We show that training a DDPM with synthetical and low-quality demonstrations is sufficient for generating nontrivial paths reaching arbitrary targets and avoiding obstacles. Additionally, we investigate different strategies for conditional sampling combining classifier-free and classifier-guided approaches. Eventually, we deploy the DDPM in a receding-horizon control scheme to enhance its planning capabilities. The Denoising Diffusion Planner is experimentally validated through various experiments on a Franka Emika Panda robot.

Sparsifying Parametric Models with L0 Regularization

This document contains an educational introduction to the problem of sparsifying parametric models with L0 regularization. We utilize this approach together with dictionary learning to learn sparse polynomial policies for deep reinforcement learning to control parametric partial differential equations. The code and a tutorial are provided here: https://github.com/nicob15/Sparsifying-Parametric-Models-with-L0.

Recurrent Deep Kernel Learning of Dynamical Systems

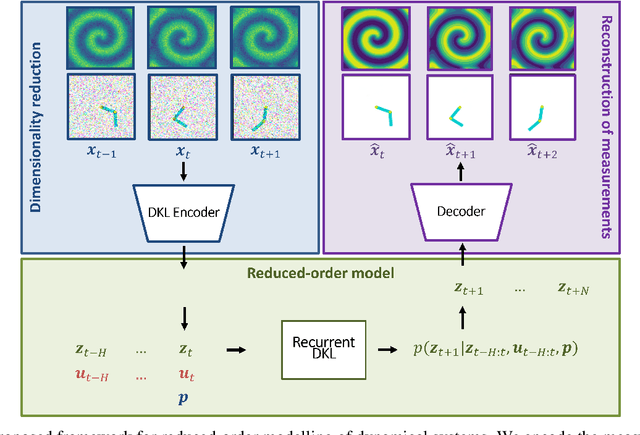
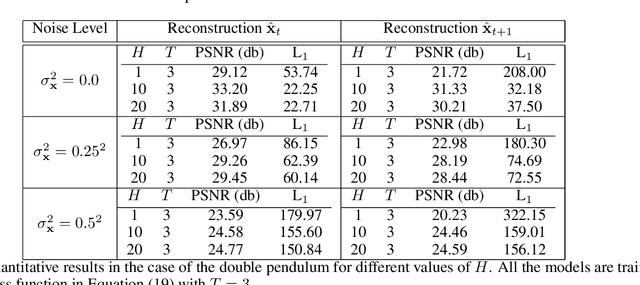
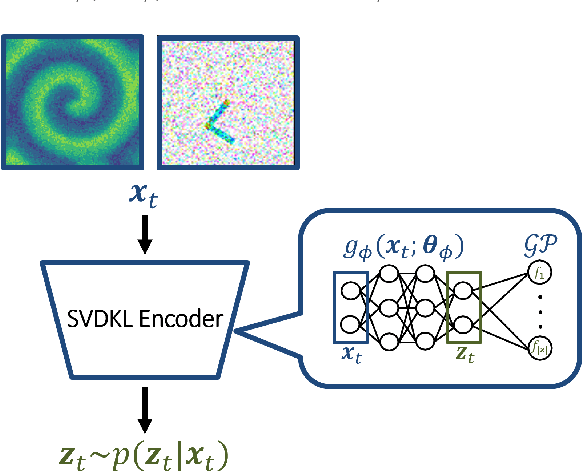
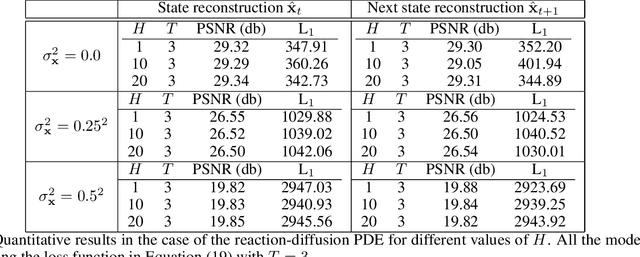
Digital twins require computationally-efficient reduced-order models (ROMs) that can accurately describe complex dynamics of physical assets. However, constructing ROMs from noisy high-dimensional data is challenging. In this work, we propose a data-driven, non-intrusive method that utilizes stochastic variational deep kernel learning (SVDKL) to discover low-dimensional latent spaces from data and a recurrent version of SVDKL for representing and predicting the evolution of latent dynamics. The proposed method is demonstrated with two challenging examples -- a double pendulum and a reaction-diffusion system. Results show that our framework is capable of (i) denoising and reconstructing measurements, (ii) learning compact representations of system states, (iii) predicting system evolution in low-dimensional latent spaces, and (iv) quantifying modeling uncertainties.

Parametric PDE Control with Deep Reinforcement Learning and Differentiable L0-Sparse Polynomial Policies

Optimal control of parametric partial differential equations (PDEs) is crucial in many applications in engineering and science. In recent years, the progress in scientific machine learning has opened up new frontiers for the control of parametric PDEs. In particular, deep reinforcement learning (DRL) has the potential to solve high-dimensional and complex control problems in a large variety of applications. Most DRL methods rely on deep neural network (DNN) control policies. However, for many dynamical systems, DNN-based control policies tend to be over-parametrized, which means they need large amounts of training data, show limited robustness, and lack interpretability. In this work, we leverage dictionary learning and differentiable L$_0$ regularization to learn sparse, robust, and interpretable control policies for parametric PDEs. Our sparse policy architecture is agnostic to the DRL method and can be used in different policy-gradient and actor-critic DRL algorithms without changing their policy-optimization procedure. We test our approach on the challenging tasks of controlling parametric Kuramoto-Sivashinsky and convection-diffusion-reaction PDEs. We show that our method (1) outperforms baseline DNN-based DRL policies, (2) allows for the derivation of interpretable equations of the learned optimal control laws, and (3) generalizes to unseen parameters of the PDE without retraining the policies.

CORE: Towards Scalable and Efficient Causal Discovery with Reinforcement Learning

Causal discovery is the challenging task of inferring causal structure from data. Motivated by Pearl's Causal Hierarchy (PCH), which tells us that passive observations alone are not enough to distinguish correlation from causation, there has been a recent push to incorporate interventions into machine learning research. Reinforcement learning provides a convenient framework for such an active approach to learning. This paper presents CORE, a deep reinforcement learning-based approach for causal discovery and intervention planning. CORE learns to sequentially reconstruct causal graphs from data while learning to perform informative interventions. Our results demonstrate that CORE generalizes to unseen graphs and efficiently uncovers causal structures. Furthermore, CORE scales to larger graphs with up to 10 variables and outperforms existing approaches in structure estimation accuracy and sample efficiency. All relevant code and supplementary material can be found at https://github.com/sa-and/CORE

Trajectory Generation, Control, and Safety with Denoising Diffusion Probabilistic Models

We present a framework for safety-critical optimal control of physical systems based on denoising diffusion probabilistic models (DDPMs). The technology of control barrier functions (CBFs), encoding desired safety constraints, is used in combination with DDPMs to plan actions by iteratively denoising trajectories through a CBF-based guided sampling procedure. At the same time, the generated trajectories are also guided to maximize a future cumulative reward representing a specific task to be optimally executed. The proposed scheme can be seen as an offline and model-based reinforcement learning algorithm resembling in its functionalities a model-predictive control optimization scheme with receding horizon in which the selected actions lead to optimal and safe trajectories.

Discovering Efficient Periodic Behaviours in Mechanical Systems via Neural Approximators

It is well known that conservative mechanical systems exhibit local oscillatory behaviours due to their elastic and gravitational potentials, which completely characterise these periodic motions together with the inertial properties of the system. The classification of these periodic behaviours and their geometric characterisation are in an on-going secular debate, which recently led to the so-called eigenmanifold theory. The eigenmanifold characterises nonlinear oscillations as a generalisation of linear eigenspaces. With the motivation of performing periodic tasks efficiently, we use tools coming from this theory to construct an optimization problem aimed at inducing desired closed-loop oscillations through a state feedback law. We solve the constructed optimization problem via gradient-descent methods involving neural networks. Extensive simulations show the validity of the approach.

Deep Kernel Learning of Dynamical Models from High-Dimensional Noisy Data

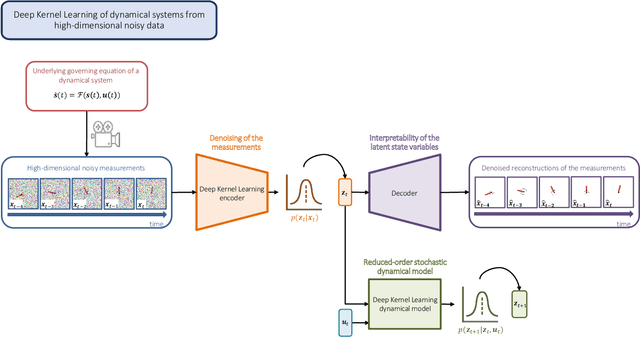
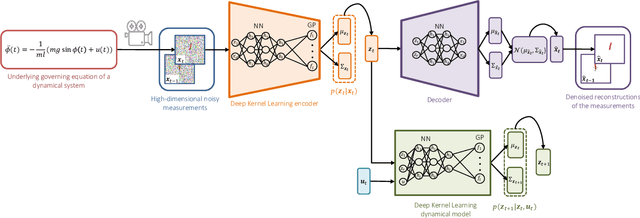
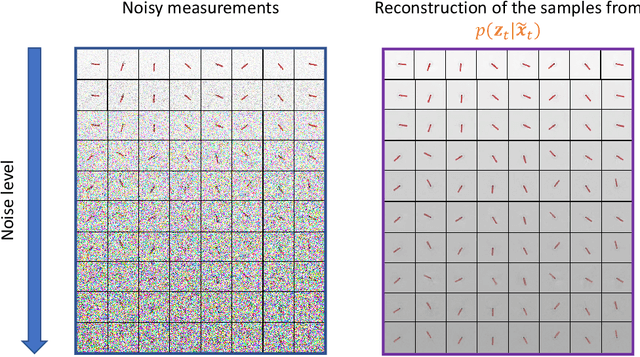
This work proposes a Stochastic Variational Deep Kernel Learning method for the data-driven discovery of low-dimensional dynamical models from high-dimensional noisy data. The framework is composed of an encoder that compresses high-dimensional measurements into low-dimensional state variables, and a latent dynamical model for the state variables that predicts the system evolution over time. The training of the proposed model is carried out in an unsupervised manner, i.e., not relying on labeled data. Our learning method is evaluated on the motion of a pendulum -- a well studied baseline for nonlinear model identification and control with continuous states and control inputs -- measured via high-dimensional noisy RGB images. Results show that the method can effectively denoise measurements, learn compact state representations and latent dynamical models, as well as identify and quantify modeling uncertainties.

Unsupervised Representation Learning in Deep Reinforcement Learning: A Review

This review addresses the problem of learning abstract representations of the measurement data in the context of Deep Reinforcement Learning (DRL). While the data are often ambiguous, high-dimensional, and complex to interpret, many dynamical systems can be effectively described by a low-dimensional set of state variables. Discovering these state variables from the data is a crucial aspect for improving the data efficiency, robustness and generalization of DRL methods, tackling the curse of dimensionality, and bringing interpretability and insights into black-box DRL. This review provides a comprehensive and complete overview of unsupervised representation learning in DRL by describing the main Deep Learning tools used for learning representations of the world, providing a systematic view of the method and principles, summarizing applications, benchmarks and evaluation strategies, and discussing open challenges and future directions.