Recurrent Deep Kernel Learning of Dynamical Systems

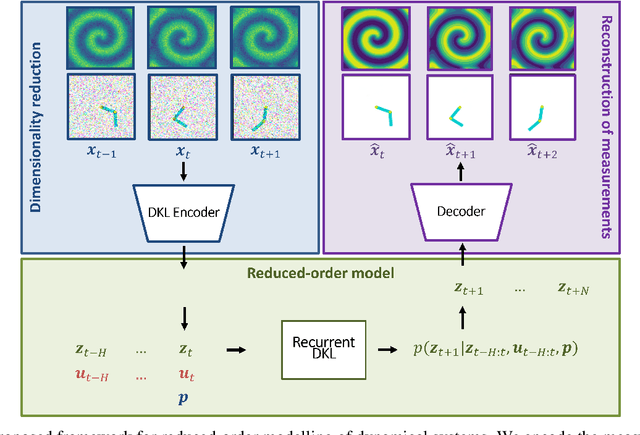
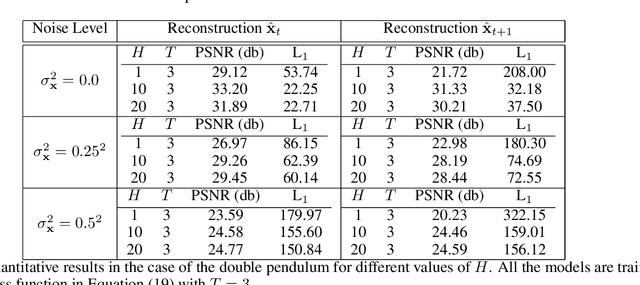
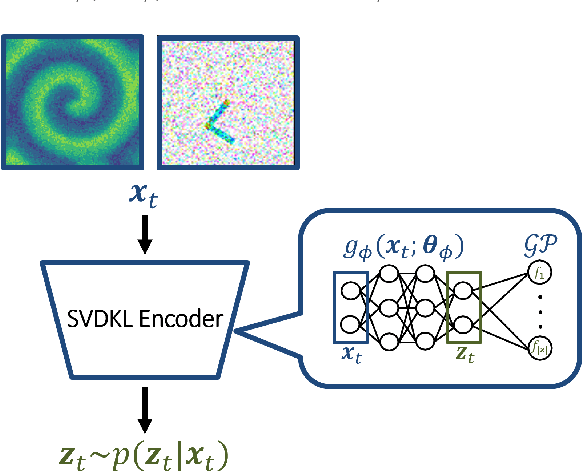
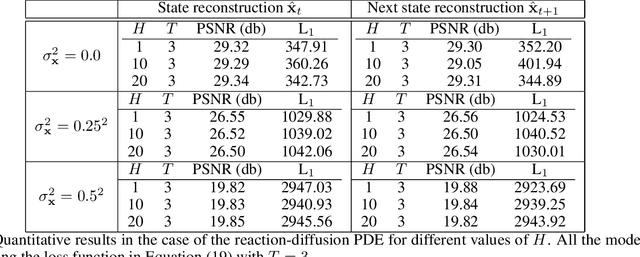
Digital twins require computationally-efficient reduced-order models (ROMs) that can accurately describe complex dynamics of physical assets. However, constructing ROMs from noisy high-dimensional data is challenging. In this work, we propose a data-driven, non-intrusive method that utilizes stochastic variational deep kernel learning (SVDKL) to discover low-dimensional latent spaces from data and a recurrent version of SVDKL for representing and predicting the evolution of latent dynamics. The proposed method is demonstrated with two challenging examples -- a double pendulum and a reaction-diffusion system. Results show that our framework is capable of (i) denoising and reconstructing measurements, (ii) learning compact representations of system states, (iii) predicting system evolution in low-dimensional latent spaces, and (iv) quantifying modeling uncertainties.

On the latent dimension of deep autoencoders for reduced order modeling of PDEs parametrized by random fields

Deep Learning is having a remarkable impact on the design of Reduced Order Models (ROMs) for Partial Differential Equations (PDEs), where it is exploited as a powerful tool for tackling complex problems for which classical methods might fail. In this respect, deep autoencoders play a fundamental role, as they provide an extremely flexible tool for reducing the dimensionality of a given problem by leveraging on the nonlinear capabilities of neural networks. Indeed, starting from this paradigm, several successful approaches have already been developed, which are here referred to as Deep Learning-based ROMs (DL-ROMs). Nevertheless, when it comes to stochastic problems parameterized by random fields, the current understanding of DL-ROMs is mostly based on empirical evidence: in fact, their theoretical analysis is currently limited to the case of PDEs depending on a finite number of (deterministic) parameters. The purpose of this work is to extend the existing literature by providing some theoretical insights about the use of DL-ROMs in the presence of stochasticity generated by random fields. In particular, we derive explicit error bounds that can guide domain practitioners when choosing the latent dimension of deep autoencoders. We evaluate the practical usefulness of our theory by means of numerical experiments, showing how our analysis can significantly impact the performance of DL-ROMs.

A Deep Learning approach to Reduced Order Modelling of Parameter Dependent Partial Differential Equations

Within the framework of parameter dependent PDEs, we develop a constructive approach based on Deep Neural Networks for the efficient approximation of the parameter-to-solution map. The research is motivated by the limitations and drawbacks of state-of-the-art algorithms, such as the Reduced Basis method, when addressing problems that show a slow decay in the Kolmogorov n-width. Our work is based on the use of deep autoencoders, which we employ for encoding and decoding a high fidelity approximation of the solution manifold. In order to fully exploit the approximation capabilities of neural networks, we consider a nonlinear version of the Kolmogorov n-width over which we base the concept of a minimal latent dimension. We show that this minimal dimension is intimately related to the topological properties of the solution manifold, and we provide some theoretical results with particular emphasis on second order elliptic PDEs. Finally, we report numerical experiments where we compare the proposed approach with classical POD-Galerkin reduced order models. In particular, we consider parametrized advection-diffusion PDEs, and we test the methodology in the presence of strong transport fields, singular terms and stochastic coefficients.

Learning High-Order Interactions via Targeted Pattern Search

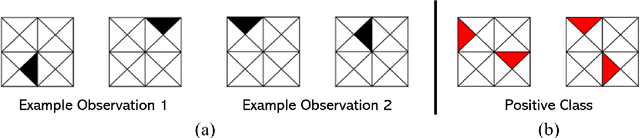
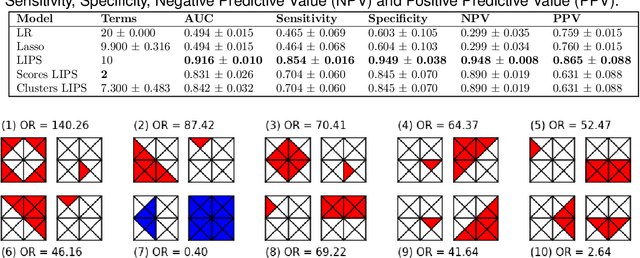
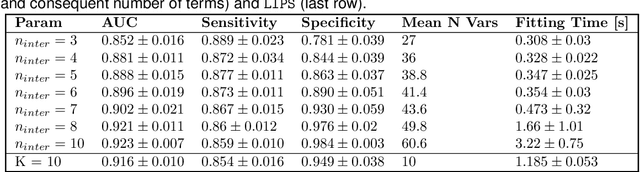
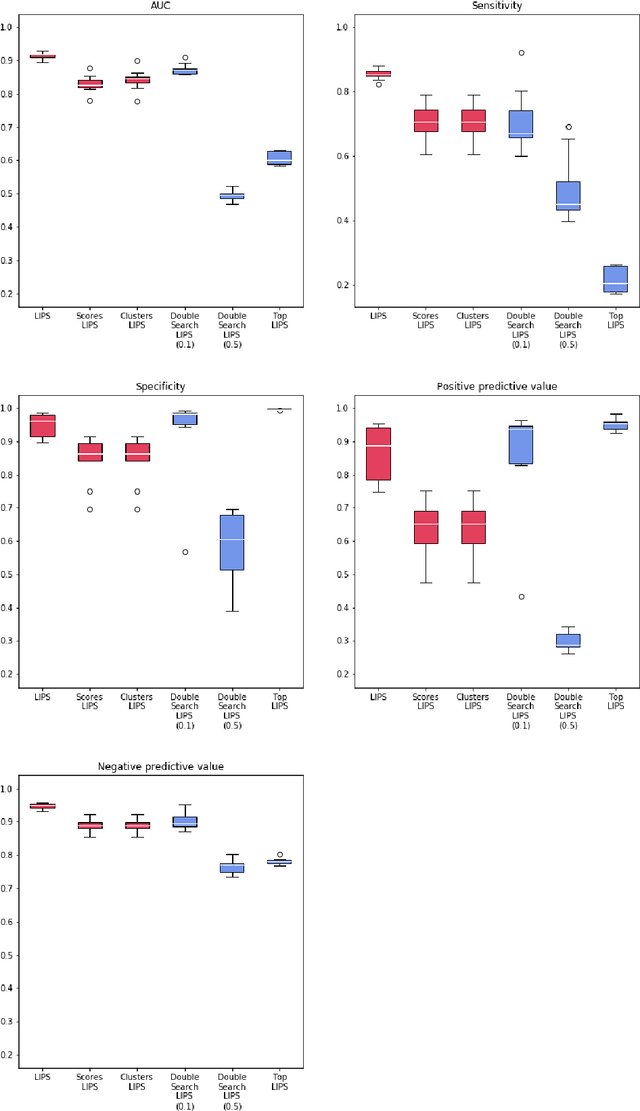
Logistic Regression (LR) is a widely used statistical method in empirical binary classification studies. However, real-life scenarios oftentimes share complexities that prevent from the use of the as-is LR model, and instead highlight the need to include high-order interactions to capture data variability. This becomes even more challenging because of: (i) datasets growing wider, with more and more variables; (ii) studies being typically conducted in strongly imbalanced settings; (iii) samples going from very large to extremely small; (iv) the need of providing both predictive models and interpretable results. In this paper we present a novel algorithm, Learning high-order Interactions via targeted Pattern Search (LIPS), to select interaction terms of varying order to include in a LR model for an imbalanced binary classification task when input data are categorical. LIPS's rationale stems from the duality between item sets and categorical interactions. The algorithm relies on an interaction learning step based on a well-known frequent item set mining algorithm, and a novel dissimilarity-based interaction selection step that allows the user to specify the number of interactions to be included in the LR model. In addition, we particularize two variants (Scores LIPS and Clusters LIPS), that can address even more specific needs. Through a set of experiments we validate our algorithm and prove its wide applicability to real-life research scenarios, showing that it outperforms a benchmark state-of-the-art algorithm.