Neural Fields for Continuous Periodic Motion Estimation in 4D Cardiovascular Imaging

Time-resolved three-dimensional flow MRI (4D flow MRI) provides a unique non-invasive solution to visualize and quantify hemodynamics in blood vessels such as the aortic arch. However, most current analysis methods for arterial 4D flow MRI use static artery walls because of the difficulty in obtaining a full cycle segmentation. To overcome this limitation, we propose a neural fields-based method that directly estimates continuous periodic wall deformations throughout the cardiac cycle. For a 3D + time imaging dataset, we optimize an implicit neural representation (INR) that represents a time-dependent velocity vector field (VVF). An ODE solver is used to integrate the VVF into a deformation vector field (DVF), that can deform images, segmentation masks, or meshes over time, thereby visualizing and quantifying local wall motion patterns. To properly reflect the periodic nature of 3D + time cardiovascular data, we impose periodicity in two ways. First, by periodically encoding the time input to the INR, and hence VVF. Second, by regularizing the DVF. We demonstrate the effectiveness of this approach on synthetic data with different periodic patterns, ECG-gated CT, and 4D flow MRI data. The obtained method could be used to improve 4D flow MRI analysis.

Defocus Blur Synthesis and Deblurring via Interpolation and Extrapolation in Latent Space

Though modern microscopes have an autofocusing system to ensure optimal focus, out-of-focus images can still occur when cells within the medium are not all in the same focal plane, affecting the image quality for medical diagnosis and analysis of diseases. We propose a method that can deblur images as well as synthesize defocus blur. We train autoencoders with implicit and explicit regularization techniques to enforce linearity relations among the representations of different blur levels in the latent space. This allows for the exploration of different blur levels of an object by linearly interpolating/extrapolating the latent representations of images taken at different focal planes. Compared to existing works, we use a simple architecture to synthesize images with flexible blur levels, leveraging the linear latent space. Our regularized autoencoders can effectively mimic blur and deblur, increasing data variety as a data augmentation technique and improving the quality of microscopic images, which would be beneficial for further processing and analysis.

RSA-INR: Riemannian Shape Autoencoding via 4D Implicit Neural Representations

Shape encoding and shape analysis are valuable tools for comparing shapes and for dimensionality reduction. A specific framework for shape analysis is the Large Deformation Diffeomorphic Metric Mapping (LDDMM) framework, which is capable of shape matching and dimensionality reduction. Researchers have recently introduced neural networks into this framework. However, these works can not match more than two objects simultaneously or have suboptimal performance in shape variability modeling. The latter limitation occurs as the works do not use state-of-the-art shape encoding methods. Moreover, the literature does not discuss the connection between the LDDMM Riemannian distance and the Riemannian geometry for deep learning literature. Our work aims to bridge this gap by demonstrating how LDDMM can integrate Riemannian geometry into deep learning. Furthermore, we discuss how deep learning solves and generalizes shape matching and dimensionality reduction formulations of LDDMM. We achieve both goals by designing a novel implicit encoder for shapes. This model extends a neural network-based algorithm for LDDMM-based pairwise registration, results in a nonlinear manifold PCA, and adds a Riemannian geometry aspect to deep learning models for shape variability modeling. Additionally, we demonstrate that the Riemannian geometry component improves the reconstruction procedure of the implicit encoder in terms of reconstruction quality and stability to noise. We hope our discussion paves the way to more research into how Riemannian geometry, shape/image analysis, and deep learning can be combined.

Generative modeling of living cells with SO-equivariant implicit neural representations

Data-driven cell tracking and segmentation methods in biomedical imaging require diverse and information-rich training data. In cases where the number of training samples is limited, synthetic computer-generated data sets can be used to improve these methods. This requires the synthesis of cell shapes as well as corresponding microscopy images using generative models. To synthesize realistic living cell shapes, the shape representation used by the generative model should be able to accurately represent fine details and changes in topology, which are common in cells. These requirements are not met by 3D voxel masks, which are restricted in resolution, and polygon meshes, which do not easily model processes like cell growth and mitosis. In this work, we propose to represent living cell shapes as level sets of signed distance functions (SDFs) which are estimated by neural networks. We optimize a fully-connected neural network to provide an implicit representation of the SDF value at any point in a 3D+time domain, conditioned on a learned latent code that is disentangled from the rotation of the cell shape. We demonstrate the effectiveness of this approach on cells that exhibit rapid deformations (Platynereis dumerilii), cells that grow and divide (C. elegans), and cells that have growing and branching filopodial protrusions (A549 human lung carcinoma cells). A quantitative evaluation using shape features, Hausdorff distance, and Dice similarity coefficients of real and synthetic cell shapes shows that our model can generate topologically plausible complex cell shapes in 3D+time with high similarity to real living cell shapes. Finally, we show how microscopy images of living cells that correspond to our generated cell shapes can be synthesized using an image-to-image model.

Discovering Efficient Periodic Behaviours in Mechanical Systems via Neural Approximators

It is well known that conservative mechanical systems exhibit local oscillatory behaviours due to their elastic and gravitational potentials, which completely characterise these periodic motions together with the inertial properties of the system. The classification of these periodic behaviours and their geometric characterisation are in an on-going secular debate, which recently led to the so-called eigenmanifold theory. The eigenmanifold characterises nonlinear oscillations as a generalisation of linear eigenspaces. With the motivation of performing periodic tasks efficiently, we use tools coming from this theory to construct an optimization problem aimed at inducing desired closed-loop oscillations through a state feedback law. We solve the constructed optimization problem via gradient-descent methods involving neural networks. Extensive simulations show the validity of the approach.

Implicit Neural Representations for Generative Modeling of Living Cell Shapes

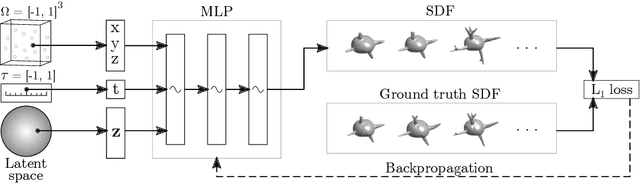
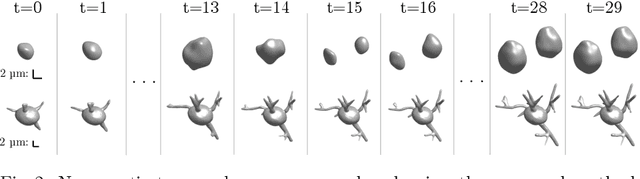
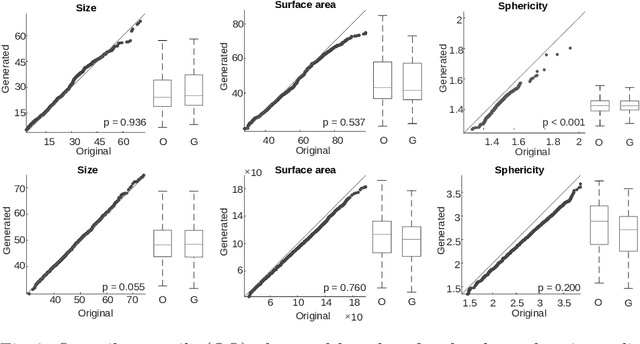
Methods allowing the synthesis of realistic cell shapes could help generate training data sets to improve cell tracking and segmentation in biomedical images. Deep generative models for cell shape synthesis require a light-weight and flexible representation of the cell shape. However, commonly used voxel-based representations are unsuitable for high-resolution shape synthesis, and polygon meshes have limitations when modeling topology changes such as cell growth or mitosis. In this work, we propose to use level sets of signed distance functions (SDFs) to represent cell shapes. We optimize a neural network as an implicit neural representation of the SDF value at any point in a 3D+time domain. The model is conditioned on a latent code, thus allowing the synthesis of new and unseen shape sequences. We validate our approach quantitatively and qualitatively on C. elegans cells that grow and divide, and lung cancer cells with growing complex filopodial protrusions. Our results show that shape descriptors of synthetic cells resemble those of real cells, and that our model is able to generate topologically plausible sequences of complex cell shapes in 3D+time.