GReAT: leveraging geometric artery data to improve wall shear stress assessment

Leveraging big data for patient care is promising in many medical fields such as cardiovascular health. For example, hemodynamic biomarkers like wall shear stress could be assessed from patient-specific medical images via machine learning algorithms, bypassing the need for time-intensive computational fluid simulation. However, it is extremely challenging to amass large-enough datasets to effectively train such models. We could address this data scarcity by means of self-supervised pre-training and foundations models given large datasets of geometric artery models. In the context of coronary arteries, leveraging learned representations to improve hemodynamic biomarker assessment has not yet been well studied. In this work, we address this gap by investigating whether a large dataset (8449 shapes) consisting of geometric models of 3D blood vessels can benefit wall shear stress assessment in coronary artery models from a small-scale clinical trial (49 patients). We create a self-supervised target for the 3D blood vessels by computing the heat kernel signature, a quantity obtained via Laplacian eigenvectors, which captures the very essence of the shapes. We show how geometric representations learned from this datasets can boost segmentation of coronary arteries into regions of low, mid and high (time-averaged) wall shear stress even when trained on limited data.

Wall Shear Stress Estimation in Abdominal Aortic Aneurysms: Towards Generalisable Neural Surrogate Models

Abdominal aortic aneurysms (AAAs) are pathologic dilatations of the abdominal aorta posing a high fatality risk upon rupture. Studying AAA progression and rupture risk often involves in-silico blood flow modelling with computational fluid dynamics (CFD) and extraction of hemodynamic factors like time-averaged wall shear stress (TAWSS) or oscillatory shear index (OSI). However, CFD simulations are known to be computationally demanding. Hence, in recent years, geometric deep learning methods, operating directly on 3D shapes, have been proposed as compelling surrogates, estimating hemodynamic parameters in just a few seconds. In this work, we propose a geometric deep learning approach to estimating hemodynamics in AAA patients, and study its generalisability to common factors of real-world variation. We propose an E(3)-equivariant deep learning model utilising novel robust geometrical descriptors and projective geometric algebra. Our model is trained to estimate transient WSS using a dataset of CT scans of 100 AAA patients, from which lumen geometries are extracted and reference CFD simulations with varying boundary conditions are obtained. Results show that the model generalizes well within the distribution, as well as to the external test set. Moreover, the model can accurately estimate hemodynamics across geometry remodelling and changes in boundary conditions. Furthermore, we find that a trained model can be applied to different artery tree topologies, where new and unseen branches are added during inference. Finally, we find that the model is to a large extent agnostic to mesh resolution. These results show the accuracy and generalisation of the proposed model, and highlight its potential to contribute to hemodynamic parameter estimation in clinical practice.

Geometric deep learning for local growth prediction on abdominal aortic aneurysm surfaces

Abdominal aortic aneurysms (AAAs) are progressive focal dilatations of the abdominal aorta. AAAs may rupture, with a survival rate of only 20\%. Current clinical guidelines recommend elective surgical repair when the maximum AAA diameter exceeds 55 mm in men or 50 mm in women. Patients that do not meet these criteria are periodically monitored, with surveillance intervals based on the maximum AAA diameter. However, this diameter does not take into account the complex relation between the 3D AAA shape and its growth, making standardized intervals potentially unfit. Personalized AAA growth predictions could improve monitoring strategies. We propose to use an SE(3)-symmetric transformer model to predict AAA growth directly on the vascular model surface enriched with local, multi-physical features. In contrast to other works which have parameterized the AAA shape, this representation preserves the vascular surface's anatomical structure and geometric fidelity. We train our model using a longitudinal dataset of 113 computed tomography angiography (CTA) scans of 24 AAA patients at irregularly sampled intervals. After training, our model predicts AAA growth to the next scan moment with a median diameter error of 1.18 mm. We further demonstrate our model's utility to identify whether a patient will become eligible for elective repair within two years (acc = 0.93). Finally, we evaluate our model's generalization on an external validation set consisting of 25 CTAs from 7 AAA patients from a different hospital. Our results show that local directional AAA growth prediction from the vascular surface is feasible and may contribute to personalized surveillance strategies.

Active Learning for Deep Learning-Based Hemodynamic Parameter Estimation

Hemodynamic parameters such as pressure and wall shear stress play an important role in diagnosis, prognosis, and treatment planning in cardiovascular diseases. These parameters can be accurately computed using computational fluid dynamics (CFD), but CFD is computationally intensive. Hence, deep learning methods have been adopted as a surrogate to rapidly estimate CFD outcomes. A drawback of such data-driven models is the need for time-consuming reference CFD simulations for training. In this work, we introduce an active learning framework to reduce the number of CFD simulations required for the training of surrogate models, lowering the barriers to their deployment in new applications. We propose three distinct querying strategies to determine for which unlabeled samples CFD simulations should be obtained. These querying strategies are based on geometrical variance, ensemble uncertainty, and adherence to the physics governing fluid dynamics. We benchmark these methods on velocity field estimation in synthetic coronary artery bifurcations and find that they allow for substantial reductions in annotation cost. Notably, we find that our strategies reduce the number of samples required by up to 50% and make the trained models more robust to difficult cases. Our results show that active learning is a feasible strategy to increase the potential of deep learning-based CFD surrogates.

Learning Hemodynamic Scalar Fields on Coronary Artery Meshes: A Benchmark of Geometric Deep Learning Models

Coronary artery disease, caused by the narrowing of coronary vessels due to atherosclerosis, is the leading cause of death worldwide. The diagnostic gold standard, fractional flow reserve (FFR), measures the trans-stenotic pressure ratio during maximal vasodilation but is invasive and costly. This has driven the development of virtual FFR (vFFR) using computational fluid dynamics (CFD) to simulate coronary flow. Geometric deep learning algorithms have shown promise for learning features on meshes, including cardiovascular research applications. This study empirically analyzes various backends for predicting vFFR fields in coronary arteries as CFD surrogates, comparing six backends for learning hemodynamics on meshes using CFD solutions as ground truth. The study has two parts: i) Using 1,500 synthetic left coronary artery bifurcations, models were trained to predict pressure-related fields for vFFR reconstruction, comparing different learning variables. ii) Using 427 patient-specific CFD simulations, experiments were repeated focusing on the best-performing learning variable from the synthetic dataset. Most backends performed well on the synthetic dataset, especially when predicting pressure drop over the manifold. Transformer-based backends outperformed others when predicting pressure and vFFR fields and were the only models achieving strong performance on patient-specific data, excelling in both average per-point error and vFFR accuracy in stenotic lesions. These results suggest geometric deep learning backends can effectively replace CFD for simple geometries, while transformer-based networks are superior for complex, heterogeneous datasets. Pressure drop was identified as the optimal network output for learning pressure-related fields.

Deep vectorised operators for pulsatile hemodynamics estimation in coronary arteries from a steady-state prior

Cardiovascular hemodynamic fields provide valuable medical decision markers for coronary artery disease. Computational fluid dynamics (CFD) is the gold standard for accurate, non-invasive evaluation of these quantities in vivo. In this work, we propose a time-efficient surrogate model, powered by machine learning, for the estimation of pulsatile hemodynamics based on steady-state priors. We introduce deep vectorised operators, a modelling framework for discretisation independent learning on infinite-dimensional function spaces. The underlying neural architecture is a neural field conditioned on hemodynamic boundary conditions. Importantly, we show how relaxing the requirement of point-wise action to permutation-equivariance leads to a family of models that can be parametrised by message passing and self-attention layers. We evaluate our approach on a dataset of 74 stenotic coronary arteries extracted from coronary computed tomography angiography (CCTA) with patient-specific pulsatile CFD simulations as ground truth. We show that our model produces accurate estimates of the pulsatile velocity and pressure while being agnostic to re-sampling of the source domain (discretisation independence). This shows that deep vectorised operators are a powerful modelling tool for cardiovascular hemodynamics estimation in coronary arteries and beyond.

ICML Topological Deep Learning Challenge 2024: Beyond the Graph Domain

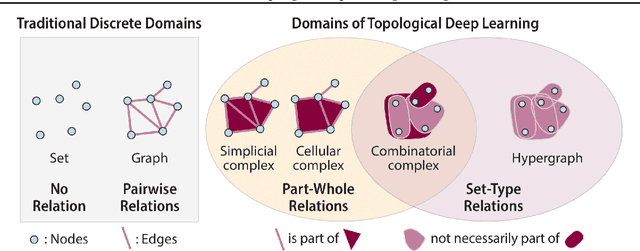
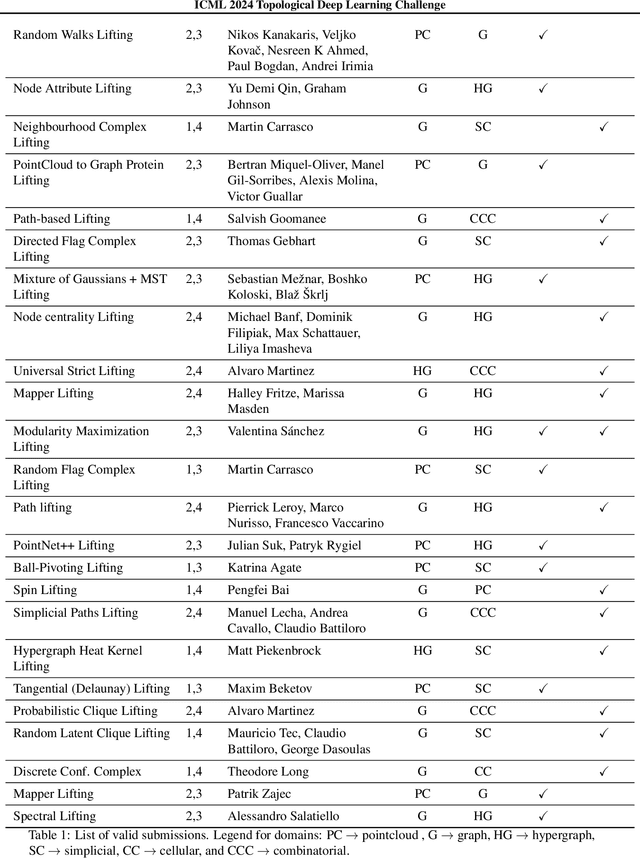
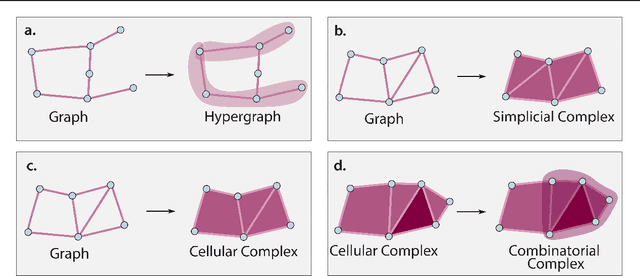
This paper describes the 2nd edition of the ICML Topological Deep Learning Challenge that was hosted within the ICML 2024 ELLIS Workshop on Geometry-grounded Representation Learning and Generative Modeling (GRaM). The challenge focused on the problem of representing data in different discrete topological domains in order to bridge the gap between Topological Deep Learning (TDL) and other types of structured datasets (e.g. point clouds, graphs). Specifically, participants were asked to design and implement topological liftings, i.e. mappings between different data structures and topological domains --like hypergraphs, or simplicial/cell/combinatorial complexes. The challenge received 52 submissions satisfying all the requirements. This paper introduces the main scope of the challenge, and summarizes the main results and findings.

LaB-GATr: geometric algebra transformers for large biomedical surface and volume meshes

Many anatomical structures can be described by surface or volume meshes. Machine learning is a promising tool to extract information from these 3D models. However, high-fidelity meshes often contain hundreds of thousands of vertices, which creates unique challenges in building deep neural network architectures. Furthermore, patient-specific meshes may not be canonically aligned which limits the generalisation of machine learning algorithms. We propose LaB-GATr, a transfomer neural network with geometric tokenisation that can effectively learn with large-scale (bio-)medical surface and volume meshes through sequence compression and interpolation. Our method extends the recently proposed geometric algebra transformer (GATr) and thus respects all Euclidean symmetries, i.e. rotation, translation and reflection, effectively mitigating the problem of canonical alignment between patients. LaB-GATr achieves state-of-the-art results on three tasks in cardiovascular hemodynamics modelling and neurodevelopmental phenotype prediction, featuring meshes of up to 200,000 vertices. Our results demonstrate that LaB-GATr is a powerful architecture for learning with high-fidelity meshes which has the potential to enable interesting downstream applications. Our implementation is publicly available.

SIRE: scale-invariant, rotation-equivariant estimation of artery orientations using graph neural networks

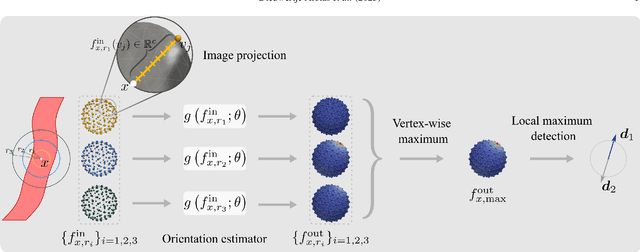
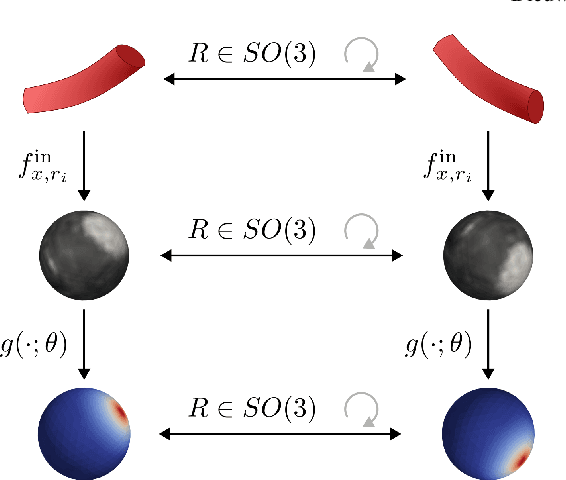
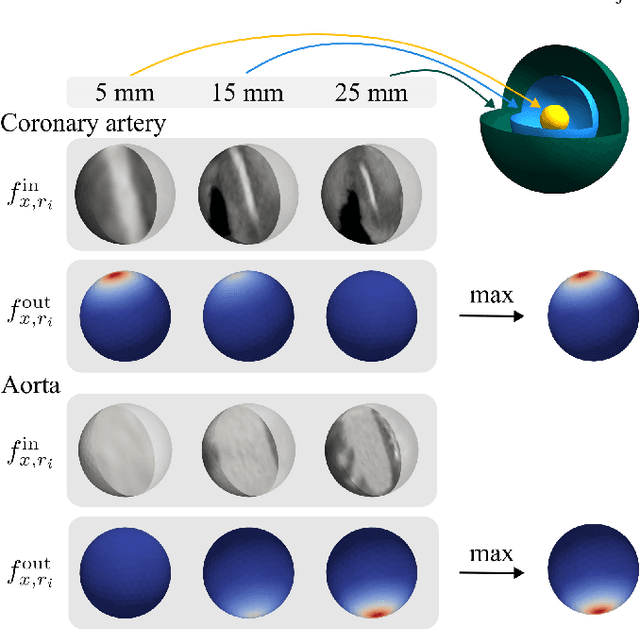
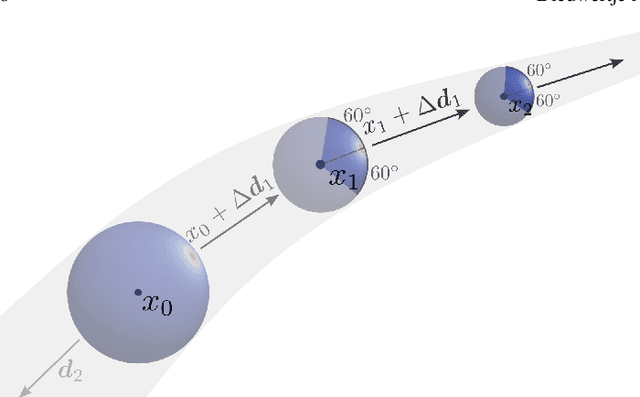
Blood vessel orientation as visualized in 3D medical images is an important descriptor of its geometry that can be used for centerline extraction and subsequent segmentation and visualization. Arteries appear at many scales and levels of tortuosity, and determining their exact orientation is challenging. Recent works have used 3D convolutional neural networks (CNNs) for this purpose, but CNNs are sensitive to varying vessel sizes and orientations. We present SIRE: a scale-invariant, rotation-equivariant estimator for local vessel orientation. SIRE is modular and can generalise due to symmetry preservation. SIRE consists of a gauge equivariant mesh CNN (GEM-CNN) operating on multiple nested spherical meshes with different sizes in parallel. The features on each mesh are a projection of image intensities within the corresponding sphere. These features are intrinsic to the sphere and, in combination with the GEM-CNN, lead to SO(3)-equivariance. Approximate scale invariance is achieved by weight sharing and use of a symmetric maximum function to combine multi-scale predictions. Hence, SIRE can be trained with arbitrarily oriented vessels with varying radii to generalise to vessels with a wide range of calibres and tortuosity. We demonstrate the efficacy of SIRE using three datasets containing vessels of varying scales: the vascular model repository (VMR), the ASOCA coronary artery set, and a set of abdominal aortic aneurysms (AAAs). We embed SIRE in a centerline tracker which accurately tracks AAAs, regardless of the data SIRE is trained with. Moreover, SIRE can be used to track coronary arteries, even when trained only with AAAs. In conclusion, by incorporating SO(3) and scale symmetries, SIRE can determine the orientations of vessels outside of the training domain, forming a robust and data-efficient solution to geometric analysis of blood vessels in 3D medical images.

Generative modeling of living cells with SO-equivariant implicit neural representations

Data-driven cell tracking and segmentation methods in biomedical imaging require diverse and information-rich training data. In cases where the number of training samples is limited, synthetic computer-generated data sets can be used to improve these methods. This requires the synthesis of cell shapes as well as corresponding microscopy images using generative models. To synthesize realistic living cell shapes, the shape representation used by the generative model should be able to accurately represent fine details and changes in topology, which are common in cells. These requirements are not met by 3D voxel masks, which are restricted in resolution, and polygon meshes, which do not easily model processes like cell growth and mitosis. In this work, we propose to represent living cell shapes as level sets of signed distance functions (SDFs) which are estimated by neural networks. We optimize a fully-connected neural network to provide an implicit representation of the SDF value at any point in a 3D+time domain, conditioned on a learned latent code that is disentangled from the rotation of the cell shape. We demonstrate the effectiveness of this approach on cells that exhibit rapid deformations (Platynereis dumerilii), cells that grow and divide (C. elegans), and cells that have growing and branching filopodial protrusions (A549 human lung carcinoma cells). A quantitative evaluation using shape features, Hausdorff distance, and Dice similarity coefficients of real and synthetic cell shapes shows that our model can generate topologically plausible complex cell shapes in 3D+time with high similarity to real living cell shapes. Finally, we show how microscopy images of living cells that correspond to our generated cell shapes can be synthesized using an image-to-image model.