A Dual Certificate Approach to Sparsity in Infinite-Width Shallow Neural Networks

In this paper, we study total variation (TV)-regularized training of infinite-width shallow ReLU neural networks, formulated as a convex optimization problem over measures on the unit sphere. Our approach leverages the duality theory of TV-regularized optimization problems to establish rigorous guarantees on the sparsity of the solutions to the training problem. Our analysis further characterizes how and when this sparsity persists in a low noise regime and for small regularization parameter. The key observation that motivates our analysis is that, for ReLU activations, the associated dual certificate is piecewise linear in the weight space. Its linearity regions, which we name dual regions, are determined by the activation patterns of the data via the induced hyperplane arrangement. Taking advantage of this structure, we prove that, on each dual region, the dual certificate admits at most one extreme value. As a consequence, the support of any minimizer is finite, and its cardinality can be bounded from above by a constant depending only on the geometry of the data-induced hyperplane arrangement. Then, we further investigate sufficient conditions ensuring uniqueness of such sparse solution. Finally, under a suitable non-degeneracy condition on the dual certificate along the boundaries of the dual regions, we prove that in the presence of low label noise and for small regularization parameter, solutions to the training problem remain sparse with the same number of Dirac deltas. Additionally, their location and the amplitudes converge, and, in case the locations lie in the interior of a dual region, the convergence happens with a rate that depends linearly on the noise and the regularization parameter.

Deep Invertible Autoencoders for Dimensionality Reduction of Dynamical Systems

Constructing reduced-order models (ROMs) capable of efficiently predicting the evolution of high-dimensional, parametric systems is crucial in many applications in engineering and applied sciences. A popular class of projection-based ROMs projects the high-dimensional full-order model (FOM) dynamics onto a low-dimensional manifold. These projection-based ROMs approaches often rely on classical model reduction techniques such as proper orthogonal decomposition (POD) or, more recently, on neural network architectures such as autoencoders (AEs). In the case that the ROM is constructed by the POD, one has approximation guaranteed based based on the singular values of the problem at hand. However, POD-based techniques can suffer from slow decay of the singular values in transport- and advection-dominated problems. In contrast to that, AEs allow for better reduction capabilities than the POD, often with the first few modes, but at the price of theoretical considerations. In addition, it is often observed, that AEs exhibits a plateau of the projection error with the increment of the dimension of the trial manifold. In this work, we propose a deep invertible AE architecture, named inv-AE, that improves upon the stagnation of the projection error typical of traditional AE architectures, e.g., convolutional, and the reconstructions quality. Inv-AE is composed of several invertible neural network layers that allows for gradually recovering more information about the FOM solutions the more we increase the dimension of the reduced manifold. Through the application of inv-AE to a parametric 1D Burgers' equation and a parametric 2D fluid flow around an obstacle with variable geometry, we show that (i) inv-AE mitigates the issue of the characteristic plateau of (convolutional) AEs and (ii) inv-AE can be combined with popular projection-based ROM approaches to improve their accuracy.

Manifold limit for the training of shallow graph convolutional neural networks

We study the discrete-to-continuum consistency of the training of shallow graph convolutional neural networks (GCNNs) on proximity graphs of sampled point clouds under a manifold assumption. Graph convolution is defined spectrally via the graph Laplacian, whose low-frequency spectrum approximates that of the Laplace-Beltrami operator of the underlying smooth manifold, and shallow GCNNs of possibly infinite width are linear functionals on the space of measures on the parameter space. From this functional-analytic perspective, graph signals are seen as spatial discretizations of functions on the manifold, which leads to a natural notion of training data consistent across graph resolutions. To enable convergence results, the continuum parameter space is chosen as a weakly compact product of unit balls, with Sobolev regularity imposed on the output weight and bias, but not on the convolutional parameter. The corresponding discrete parameter spaces inherit the corresponding spectral decay, and are additionally restricted by a frequency cutoff adapted to the informative spectral window of the graph Laplacians. Under these assumptions, we prove $Γ$-convergence of regularized empirical risk minimization functionals and corresponding convergence of their global minimizers, in the sense of weak convergence of the parameter measures and uniform convergence of the functions over compact sets. This provides a formalization of mesh and sample independence for the training of such networks.

Physics-based deep kernel learning for parameter estimation in high dimensional PDEs

Inferring parameters of high-dimensional partial differential equations (PDEs) poses significant computational and inferential challenges, primarily due to the curse of dimensionality and the inherent limitations of traditional numerical methods. This paper introduces a novel two-stage Bayesian framework that synergistically integrates training, physics-based deep kernel learning (DKL) with Hamiltonian Monte Carlo (HMC) to robustly infer unknown PDE parameters and quantify their uncertainties from sparse, exact observations. The first stage leverages physics-based DKL to train a surrogate model, which jointly yields an optimized neural network feature extractor and robust initial estimates for the PDE parameters. In the second stage, with the neural network weights fixed, HMC is employed within a full Bayesian framework to efficiently sample the joint posterior distribution of the kernel hyperparameters and the PDE parameters. Numerical experiments on canonical and high-dimensional inverse PDE problems demonstrate that our framework accurately estimates parameters, provides reliable uncertainty estimates, and effectively addresses challenges of data sparsity and model complexity, offering a robust and scalable tool for diverse scientific and engineering applications.

Consistent View Alignment Improves Foundation Models for 3D Medical Image Segmentation

Many recent approaches in representation learning implicitly assume that uncorrelated views of a data point are sufficient to learn meaningful representations for various downstream tasks. In this work, we challenge this assumption and demonstrate that meaningful structure in the latent space does not emerge naturally. Instead, it must be explicitly induced. We propose a method that aligns representations from different views of the data to align complementary information without inducing false positives. Our experiments show that our proposed self-supervised learning method, Consistent View Alignment, improves performance for downstream tasks, highlighting the critical role of structured view alignment in learning effective representations. Our method achieved first and second place in the MICCAI 2025 SSL3D challenge when using a Primus vision transformer and ResEnc convolutional neural network, respectively. The code and pretrained model weights are released at https://github.com/Tenbatsu24/LatentCampus.

An invertible generative model for forward and inverse problems

We formulate the inverse problem in a Bayesian framework and aim to train a generative model that allows us to simulate (i.e., sample from the likelihood) and do inference (i.e., sample from the posterior). We review the use of triangular normalizing flows for conditional sampling in this context and show how to combine two such triangular maps (an upper and a lower one) in to one invertible mapping that can be used for simulation and inference. We work out several useful properties of this invertible generative model and propose a possible training loss for training the map directly. We illustrate the workings of this new approach to conditional generative modeling numerically on a few stylized examples.

Wall Shear Stress Estimation in Abdominal Aortic Aneurysms: Towards Generalisable Neural Surrogate Models

Abdominal aortic aneurysms (AAAs) are pathologic dilatations of the abdominal aorta posing a high fatality risk upon rupture. Studying AAA progression and rupture risk often involves in-silico blood flow modelling with computational fluid dynamics (CFD) and extraction of hemodynamic factors like time-averaged wall shear stress (TAWSS) or oscillatory shear index (OSI). However, CFD simulations are known to be computationally demanding. Hence, in recent years, geometric deep learning methods, operating directly on 3D shapes, have been proposed as compelling surrogates, estimating hemodynamic parameters in just a few seconds. In this work, we propose a geometric deep learning approach to estimating hemodynamics in AAA patients, and study its generalisability to common factors of real-world variation. We propose an E(3)-equivariant deep learning model utilising novel robust geometrical descriptors and projective geometric algebra. Our model is trained to estimate transient WSS using a dataset of CT scans of 100 AAA patients, from which lumen geometries are extracted and reference CFD simulations with varying boundary conditions are obtained. Results show that the model generalizes well within the distribution, as well as to the external test set. Moreover, the model can accurately estimate hemodynamics across geometry remodelling and changes in boundary conditions. Furthermore, we find that a trained model can be applied to different artery tree topologies, where new and unseen branches are added during inference. Finally, we find that the model is to a large extent agnostic to mesh resolution. These results show the accuracy and generalisation of the proposed model, and highlight its potential to contribute to hemodynamic parameter estimation in clinical practice.

Geometric deep learning for local growth prediction on abdominal aortic aneurysm surfaces

Abdominal aortic aneurysms (AAAs) are progressive focal dilatations of the abdominal aorta. AAAs may rupture, with a survival rate of only 20\%. Current clinical guidelines recommend elective surgical repair when the maximum AAA diameter exceeds 55 mm in men or 50 mm in women. Patients that do not meet these criteria are periodically monitored, with surveillance intervals based on the maximum AAA diameter. However, this diameter does not take into account the complex relation between the 3D AAA shape and its growth, making standardized intervals potentially unfit. Personalized AAA growth predictions could improve monitoring strategies. We propose to use an SE(3)-symmetric transformer model to predict AAA growth directly on the vascular model surface enriched with local, multi-physical features. In contrast to other works which have parameterized the AAA shape, this representation preserves the vascular surface's anatomical structure and geometric fidelity. We train our model using a longitudinal dataset of 113 computed tomography angiography (CTA) scans of 24 AAA patients at irregularly sampled intervals. After training, our model predicts AAA growth to the next scan moment with a median diameter error of 1.18 mm. We further demonstrate our model's utility to identify whether a patient will become eligible for elective repair within two years (acc = 0.93). Finally, we evaluate our model's generalization on an external validation set consisting of 25 CTAs from 7 AAA patients from a different hospital. Our results show that local directional AAA growth prediction from the vascular surface is feasible and may contribute to personalized surveillance strategies.

Joint Manifold Learning and Optimal Transport for Dynamic Imaging

Dynamic imaging is critical for understanding and visualizing dynamic biological processes in medicine and cell biology. These applications often encounter the challenge of a limited amount of time series data and time points, which hinders learning meaningful patterns. Regularization methods provide valuable prior knowledge to address this challenge, enabling the extraction of relevant information despite the scarcity of time-series data and time points. In particular, low-dimensionality assumptions on the image manifold address sample scarcity, while time progression models, such as optimal transport (OT), provide priors on image development to mitigate the lack of time points. Existing approaches using low-dimensionality assumptions disregard a temporal prior but leverage information from multiple time series. OT-prior methods, however, incorporate the temporal prior but regularize only individual time series, ignoring information from other time series of the same image modality. In this work, we investigate the effect of integrating a low-dimensionality assumption of the underlying image manifold with an OT regularizer for time-evolving images. In particular, we propose a latent model representation of the underlying image manifold and promote consistency between this representation, the time series data, and the OT prior on the time-evolving images. We discuss the advantages of enriching OT interpolations with latent models and integrating OT priors into latent models.

Data-Agnostic Augmentations for Unknown Variations: Out-of-Distribution Generalisation in MRI Segmentation

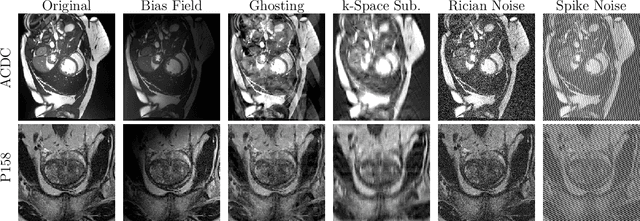
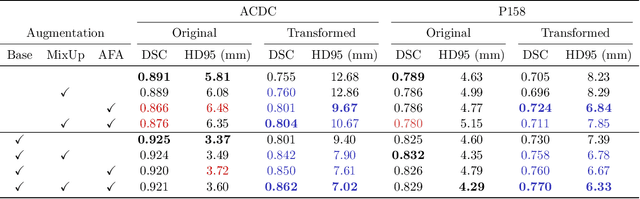
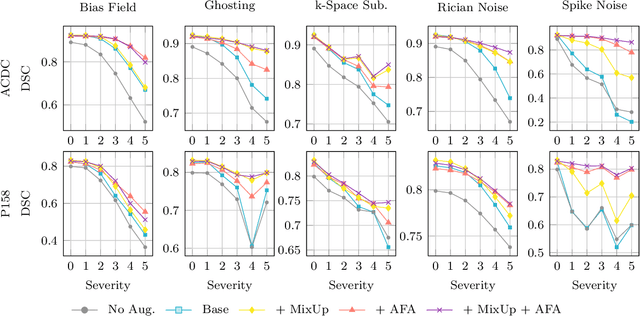
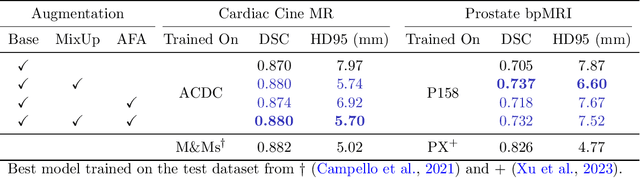
Medical image segmentation models are often trained on curated datasets, leading to performance degradation when deployed in real-world clinical settings due to mismatches between training and test distributions. While data augmentation techniques are widely used to address these challenges, traditional visually consistent augmentation strategies lack the robustness needed for diverse real-world scenarios. In this work, we systematically evaluate alternative augmentation strategies, focusing on MixUp and Auxiliary Fourier Augmentation. These methods mitigate the effects of multiple variations without explicitly targeting specific sources of distribution shifts. We demonstrate how these techniques significantly improve out-of-distribution generalization and robustness to imaging variations across a wide range of transformations in cardiac cine MRI and prostate MRI segmentation. We quantitatively find that these augmentation methods enhance learned feature representations by promoting separability and compactness. Additionally, we highlight how their integration into nnU-Net training pipelines provides an easy-to-implement, effective solution for enhancing the reliability of medical segmentation models in real-world applications.