Robust Recurrent Neural Network to Identify Ship Motion in Open Water with Performance Guarantees -- Technical Report

Recurrent neural networks are capable of learning the dynamics of an unknown nonlinear system purely from input-output measurements. However, the resulting models do not provide any stability guarantees on the input-output mapping. In this work, we represent a recurrent neural network as a linear time-invariant system with nonlinear disturbances. By introducing constraints on the parameters, we can guarantee finite gain stability and incremental finite gain stability. We apply this identification method to learn the motion of a four-degrees-of-freedom ship that is moving in open water and compare it against other purely learning-based approaches with unconstrained parameters. Our analysis shows that the constrained recurrent neural network has a lower prediction accuracy on the test set, but it achieves comparable results on an out-of-distribution set and respects stability conditions.

Certified machine learning: Rigorous a posteriori error bounds for PDE defined PINNs

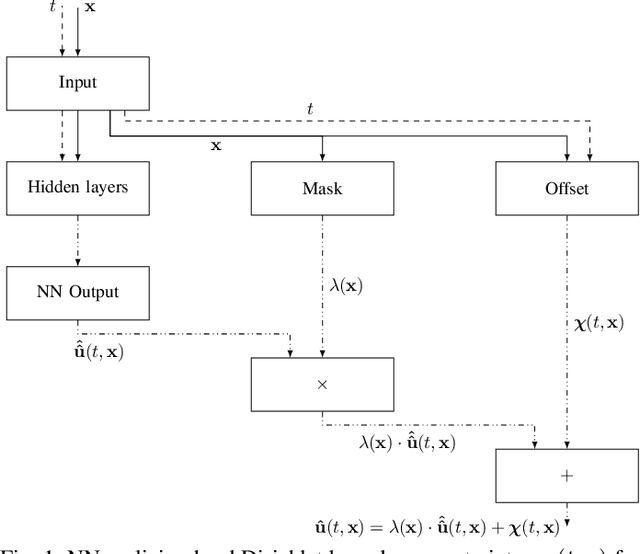
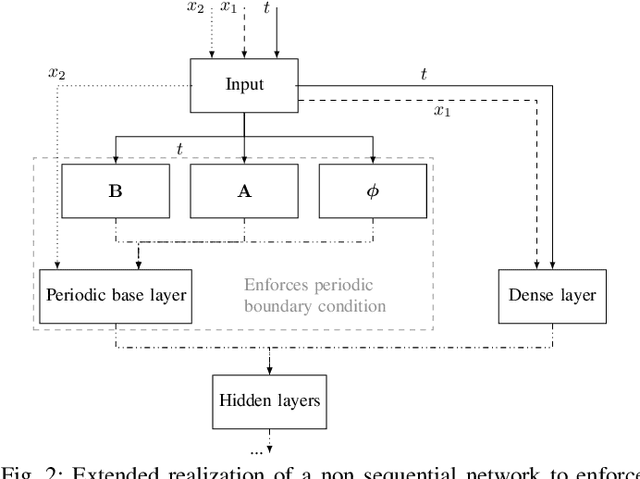
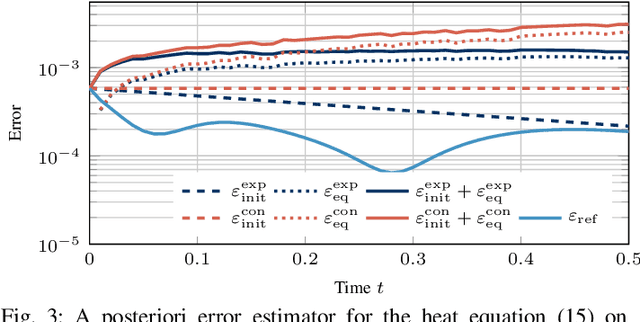
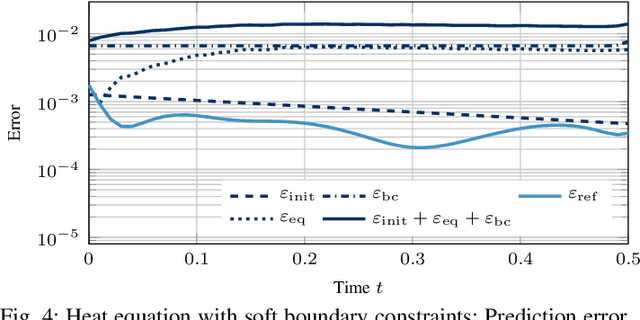
Prediction error quantification in machine learning has been left out of most methodological investigations of neural networks, for both purely data-driven and physics-informed approaches. Beyond statistical investigations and generic results on the approximation capabilities of neural networks, we present a rigorous upper bound on the prediction error of physics-informed neural networks. This bound can be calculated without the knowledge of the true solution and only with a priori available information about the characteristics of the underlying dynamical system governed by a partial differential equation. We apply this a posteriori error bound exemplarily to four problems: the transport equation, the heat equation, the Navier-Stokes equation and the Klein-Gordon equation.

Certified machine learning: A posteriori error estimation for physics-informed neural networks

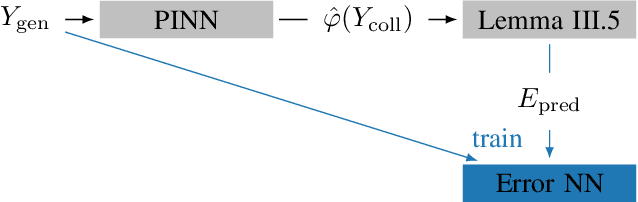
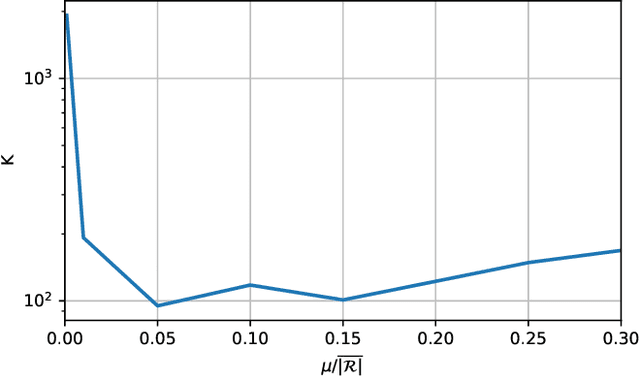
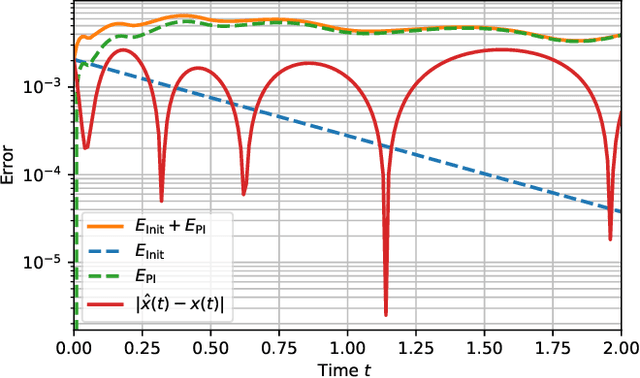
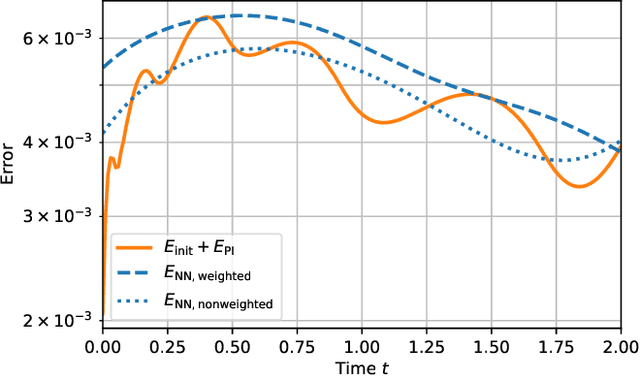
Physics-informed neural networks (PINNs) are one popular approach to introduce a priori knowledge about physical systems into the learning framework. PINNs are known to be robust for smaller training sets, derive better generalization problems, and are faster to train. In this paper, we show that using PINNs in comparison with purely data-driven neural networks is not only favorable for training performance but allows us to extract significant information on the quality of the approximated solution. Assuming that the underlying differential equation for the PINN training is an ordinary differential equation, we derive a rigorous upper limit on the PINN prediction error. This bound is applicable even for input data not included in the training phase and without any prior knowledge about the true solution. Therefore, our a posteriori error estimation is an essential step to certify the PINN. We apply our error estimator exemplarily to two academic toy problems, whereof one falls in the category of model-predictive control and thereby shows the practical use of the derived results.

Physics-informed Neural Networks-based Model Predictive Control for Multi-link Manipulators

We discuss nonlinear model predictive control (NMPC) for multi-body dynamics via physics-informed machine learning methods. Physics-informed neural networks (PINNs) are a promising tool to approximate (partial) differential equations. PINNs are not suited for control tasks in their original form since they are not designed to handle variable control actions or variable initial values. We thus present the idea of enhancing PINNs by adding control actions and initial conditions as additional network inputs. The high-dimensional input space is subsequently reduced via a sampling strategy and a zero-hold assumption. This strategy enables the controller design based on a PINN as an approximation of the underlying system dynamics. The additional benefit is that the sensitivities are easily computed via automatic differentiation, thus leading to efficient gradient-based algorithms. Finally, we present our results using our PINN-based MPC to solve a tracking problem for a complex mechanical system, a multi-link manipulator.