Deep subspace encoders for continuous-time state-space identification

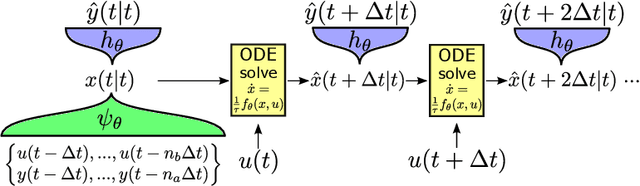
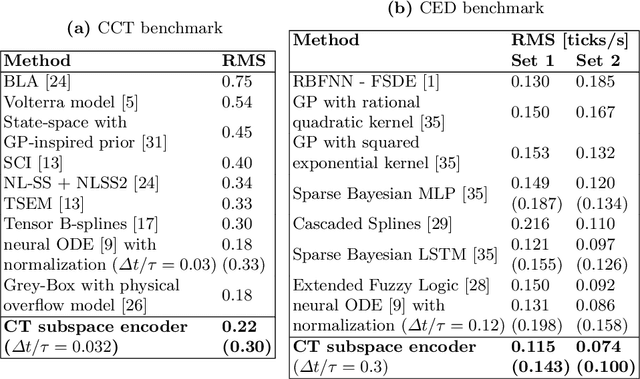
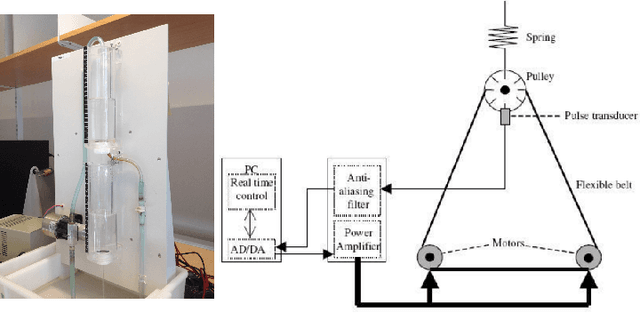
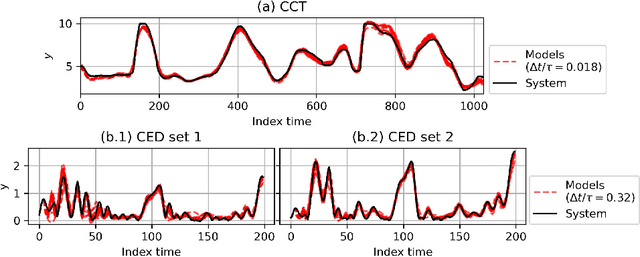
Continuous-time (CT) models have shown an improved sample efficiency during learning and enable ODE analysis methods for enhanced interpretability compared to discrete-time (DT) models. Even with numerous recent developments, the multifaceted CT state-space model identification problem remains to be solved in full, considering common experimental aspects such as the presence of external inputs, measurement noise, and latent states. This paper presents a novel estimation method that includes these aspects and that is able to obtain state-of-the-art results on multiple benchmarks where a small fully connected neural network describes the CT dynamics. The novel estimation method called the subspace encoder approach ascertains these results by altering the well-known simulation loss to include short subsections instead, by using an encoder function and a state-derivative normalization term to obtain a computationally feasible and stable optimization problem. This encoder function estimates the initial states of each considered subsection. We prove that the existence of the encoder function has the necessary condition of a Lipschitz continuous state-derivative utilizing established properties of ODEs.

Deep Identification of Nonlinear Systems in Koopman Form

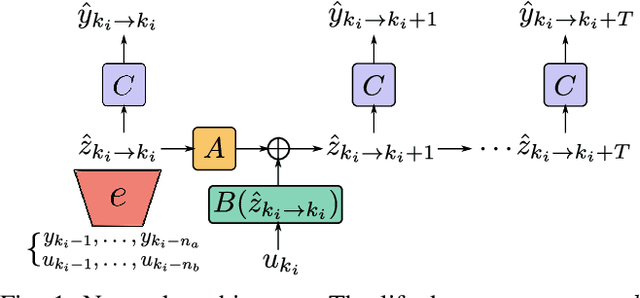
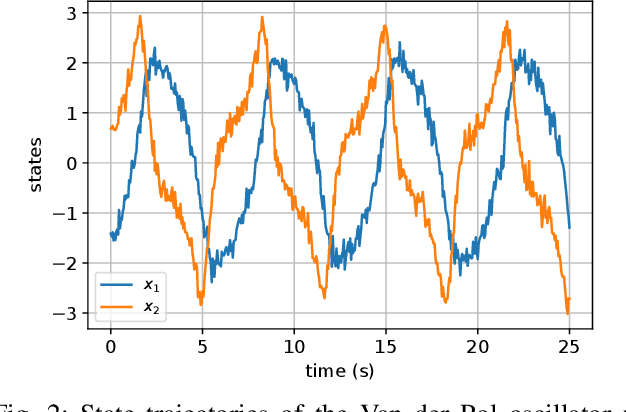
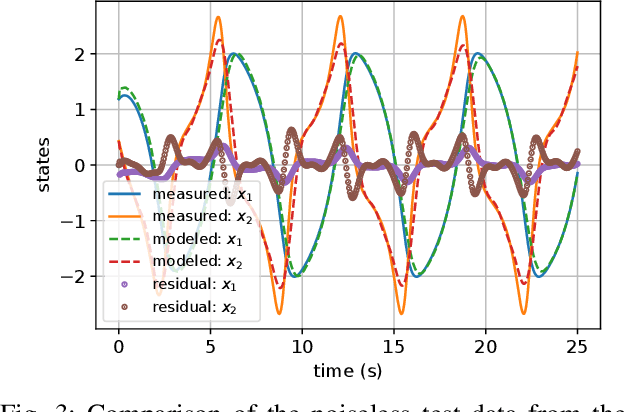
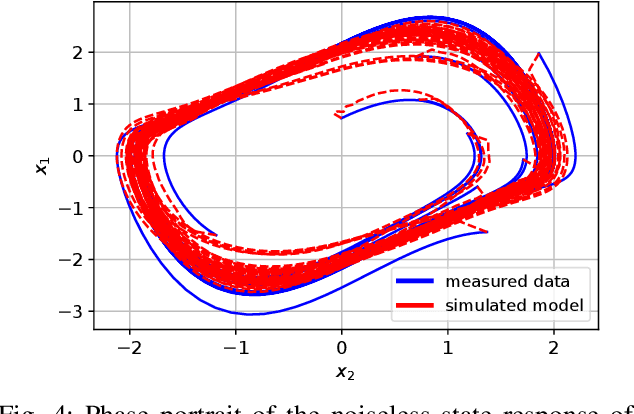
The present paper treats the identification of nonlinear dynamical systems using Koopman-based deep state-space encoders. Through this method, the usual drawback of needing to choose a dictionary of lifting functions a priori is circumvented. The encoder represents the lifting function to the space where the dynamics are linearly propagated using the Koopman operator. An input-affine formulation is considered for the lifted model structure and we address both full and partial state availability. The approach is implemented using the the deepSI toolbox in Python. To lower the computational need of the simulation error-based training, the data is split into subsections where multi-step prediction errors are calculated independently. This formulation allows for efficient batch optimization of the network parameters and, at the same time, excellent long term prediction capabilities of the obtained models. The performance of the approach is illustrated by nonlinear benchmark examples.

Non-linear State-space Model Identification from Video Data using Deep Encoders

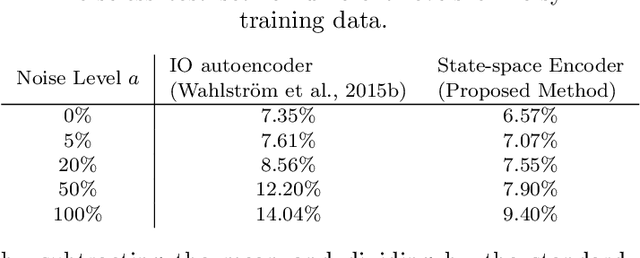
Identifying systems with high-dimensional inputs and outputs, such as systems measured by video streams, is a challenging problem with numerous applications in robotics, autonomous vehicles and medical imaging. In this paper, we propose a novel non-linear state-space identification method starting from high-dimensional input and output data. Multiple computational and conceptual advances are combined to handle the high-dimensional nature of the data. An encoder function, represented by a neural network, is introduced to learn a reconstructability map to estimate the model states from past inputs and outputs. This encoder function is jointly learned with the dynamics. Furthermore, multiple computational improvements, such as an improved reformulation of multiple shooting and batch optimization, are proposed to keep the computational time under control when dealing with high-dimensional and large datasets. We apply the proposed method to a video stream of a simulated environment of a controllable ball in a unit box. The simulation study shows low simulation error with excellent long term prediction for the obtained model using the proposed method.