Nonparametric Control-Koopman Operator Learning: Flexible and Scalable Models for Prediction and Control

Linearity of Koopman operators and simplicity of their estimators coupled with model-reduction capabilities has lead to their great popularity in applications for learning dynamical systems. While nonparametric Koopman operator learning in infinite-dimensional reproducing kernel Hilbert spaces is well understood for autonomous systems, its control system analogues are largely unexplored. Addressing systems with control inputs in a principled manner is crucial for fully data-driven learning of controllers, especially since existing approaches commonly resort to representational heuristics or parametric models of limited expressiveness and scalability. We address the aforementioned challenge by proposing a universal framework via control-affine reproducing kernels that enables direct estimation of a single operator even for control systems. The proposed approach, called control-Koopman operator regression (cKOR), is thus completely analogous to Koopman operator regression of the autonomous case. First in the literature, we present a nonparametric framework for learning Koopman operator representations of nonlinear control-affine systems that does not suffer from the curse of control input dimensionality. This allows for reformulating the infinite-dimensional learning problem in a finite-dimensional space based solely on data without apriori loss of precision due to a restriction to a finite span of functions or inputs as in other approaches. For enabling applications to large-scale control systems, we also enhance the scalability of control-Koopman operator estimators by leveraging random projections (sketching). The efficacy of our novel cKOR approach is demonstrated on both forecasting and control tasks.

Deep Identification of Nonlinear Systems in Koopman Form

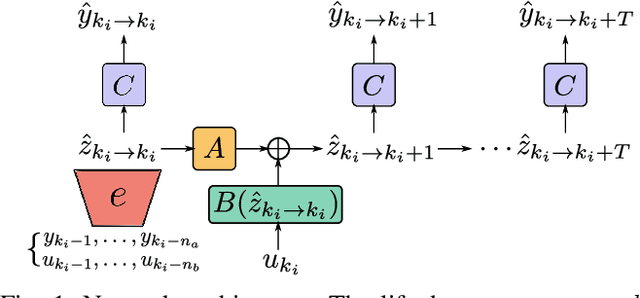
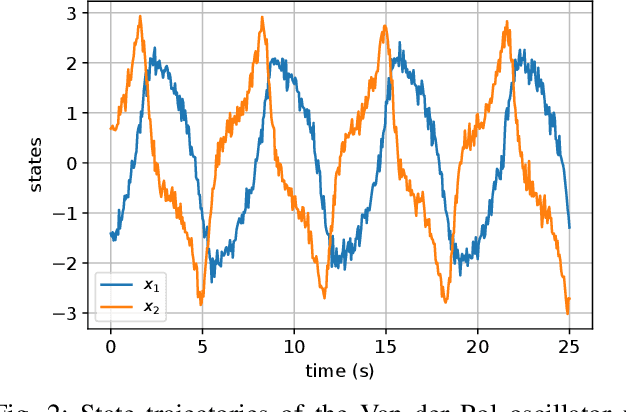
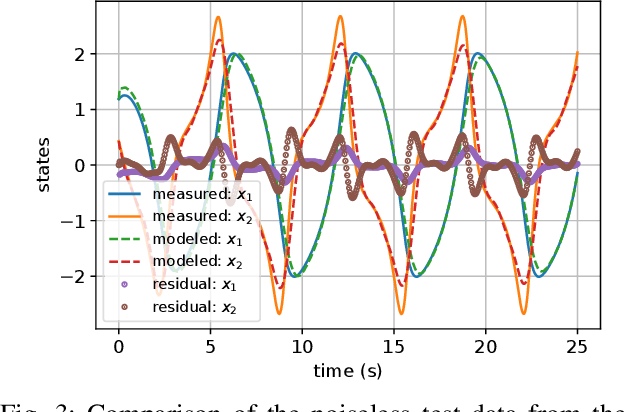
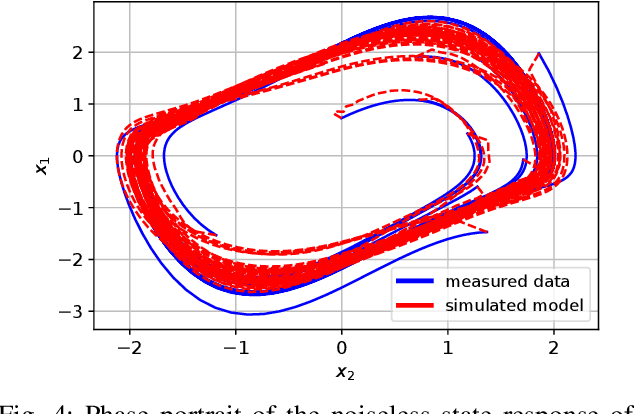
The present paper treats the identification of nonlinear dynamical systems using Koopman-based deep state-space encoders. Through this method, the usual drawback of needing to choose a dictionary of lifting functions a priori is circumvented. The encoder represents the lifting function to the space where the dynamics are linearly propagated using the Koopman operator. An input-affine formulation is considered for the lifted model structure and we address both full and partial state availability. The approach is implemented using the the deepSI toolbox in Python. To lower the computational need of the simulation error-based training, the data is split into subsections where multi-step prediction errors are calculated independently. This formulation allows for efficient batch optimization of the network parameters and, at the same time, excellent long term prediction capabilities of the obtained models. The performance of the approach is illustrated by nonlinear benchmark examples.