Adaptive Sensor Steering Strategy Using Deep Reinforcement Learning for Dynamic Data Acquisition in Digital Twins

This paper introduces a sensor steering methodology based on deep reinforcement learning to enhance the predictive accuracy and decision support capabilities of digital twins by optimising the data acquisition process. Traditional sensor placement techniques are often constrained by one-off optimisation strategies, which limit their applicability for online applications requiring continuous informative data assimilation. The proposed approach addresses this limitation by offering an adaptive framework for sensor placement within the digital twin paradigm. The sensor placement problem is formulated as a Markov decision process, enabling the training and deployment of an agent capable of dynamically repositioning sensors in response to the evolving conditions of the physical structure as represented by the digital twin. This ensures that the digital twin maintains a highly representative and reliable connection to its physical counterpart. The proposed framework is validated through a series of comprehensive case studies involving a cantilever plate structure subjected to diverse conditions, including healthy and damaged conditions. The results demonstrate the capability of the deep reinforcement learning agent to adaptively reposition sensors improving the quality of data acquisition and hence enhancing the overall accuracy of digital twins.

Cost-informed dimensionality reduction for structural digital twin technologies

Classification models are a key component of structural digital twin technologies used for supporting asset management decision-making. An important consideration when developing classification models is the dimensionality of the input, or feature space, used. If the dimensionality is too high, then the `curse of dimensionality' may rear its ugly head; manifesting as reduced predictive performance. To mitigate such effects, practitioners can employ dimensionality reduction techniques. The current paper formulates a decision-theoretic approach to dimensionality reduction for structural asset management. In this approach, the aim is to keep incurred misclassification costs to a minimum, as the dimensionality is reduced and discriminatory information may be lost. This formulation is constructed as an eigenvalue problem, with separabilities between classes weighted according to the cost of misclassifying them when considered in the context of a decision process. The approach is demonstrated using a synthetic case study.

Active learning for regression in engineering populations: A risk-informed approach

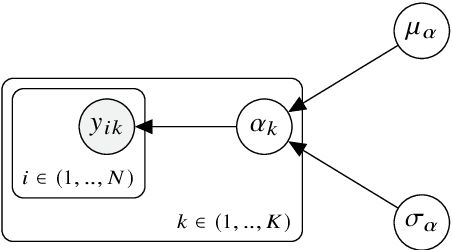
Regression is a fundamental prediction task common in data-centric engineering applications that involves learning mappings between continuous variables. In many engineering applications (e.g.\ structural health monitoring), feature-label pairs used to learn such mappings are of limited availability which hinders the effectiveness of traditional supervised machine learning approaches. The current paper proposes a methodology for overcoming the issue of data scarcity by combining active learning with hierarchical Bayesian modelling. Active learning is an approach for preferentially acquiring feature-label pairs in a resource-efficient manner. In particular, the current work adopts a risk-informed approach that leverages contextual information associated with regression-based engineering decision-making tasks (e.g.\ inspection and maintenance). Hierarchical Bayesian modelling allow multiple related regression tasks to be learned over a population, capturing local and global effects. The information sharing facilitated by this modelling approach means that information acquired for one engineering system can improve predictive performance across the population. The proposed methodology is demonstrated using an experimental case study. Specifically, multiple regressions are performed over a population of machining tools, where the quantity of interest is the surface roughness of the workpieces. An inspection and maintenance decision process is defined using these regression tasks which is in turn used to construct the active-learning algorithm. The novel methodology proposed is benchmarked against an uninformed approach to label acquisition and independent modelling of the regression tasks. It is shown that the proposed approach has superior performance in terms of expected cost -- maintaining predictive performance while reducing the number of inspections required.

A new perspective on Bayesian Operational Modal Analysis

In the field of operational modal analysis (OMA), obtained modal information is frequently used to assess the current state of aerospace, mechanical, offshore and civil structures. However, the stochasticity of operational systems and the lack of forcing information can lead to inconsistent results. Quantifying the uncertainty of the recovered modal parameters through OMA is therefore of significant value. In this article, a new perspective on Bayesian OMA is proposed: a Bayesian stochastic subspace identification (SSI) algorithm. Distinct from existing approaches to Bayesian OMA, a hierarchical probabilistic model is embedded at the core of covariance-driven SSI. Through substitution of canonical correlation analysis with a Bayesian equivalent, posterior distributions over the modal properties are obtained. Two inference schemes are presented for the proposed Bayesian formulation: Markov Chain Monte Carlo and variational Bayes. Two case studies are then explored. The first is benchmark study using data from a simulated, multi degree-of-freedom, linear system. Following application of Bayesian SSI, it is shown that the same posterior is targeted and recovered by both inference schemes, with good agreement between the posterior mean and the conventional SSI result. The second study applies the variational form to data obtained from an in-service structure: The Z24 bridge. The results of this study are presented at single model orders, and then using a stabilisation diagram. The recovered posterior uncertainty is presented and compared to the classic SSI result. It is observed that the posterior distributions with mean values coinciding with the natural frequencies exhibit lower variance than values situated away from the natural frequencies.

BINDy -- Bayesian identification of nonlinear dynamics with reversible-jump Markov-chain Monte-Carlo

Model parsimony is an important \emph{cognitive bias} in data-driven modelling that aids interpretability and helps to prevent over-fitting. Sparse identification of nonlinear dynamics (SINDy) methods are able to learn sparse representations of complex dynamics directly from data, given a basis of library functions. In this work, a novel Bayesian treatment of dictionary learning system identification, as an alternative to SINDy, is envisaged. The proposed method -- Bayesian identification of nonlinear dynamics (BINDy) -- is distinct from previous approaches in that it targets the full joint posterior distribution over both the terms in the library and their parameterisation in the model. This formulation confers the advantage that an arbitrary prior may be placed over the model structure to produce models that are sparse in the model space rather than in parameter space. Because this posterior is defined over parameter vectors that can change in dimension, the inference cannot be performed by standard techniques. Instead, a Gibbs sampler based on reversible-jump Markov-chain Monte-Carlo is proposed. BINDy is shown to compare favourably to ensemble SINDy in three benchmark case-studies. In particular, it is seen that the proposed method is better able to assign high probability to correct model terms.

Multiple-input, multiple-output modal testing of a Hawk T1A aircraft: A new full-scale dataset for structural health monitoring

The use of measured vibration data from structures has a long history of enabling the development of methods for inference and monitoring. In particular, applications based on system identification and structural health monitoring have risen to prominence over recent decades and promise significant benefits when implemented in practice. However, significant challenges remain in the development of these methods. The introduction of realistic, full-scale datasets will be an important contribution to overcoming these challenges. This paper presents a new benchmark dataset capturing the dynamic response of a decommissioned BAE Systems Hawk T1A. The dataset reflects the behaviour of a complex structure with a history of service that can still be tested in controlled laboratory conditions, using a variety of known loading and damage simulation conditions. As such, it provides a key stepping stone between simple laboratory test structures and in-service structures. In this paper, the Hawk structure is described in detail, alongside a comprehensive summary of the experimental work undertaken. Following this, key descriptive highlights of the dataset are presented, before a discussion of the research challenges that the data present. Using the dataset, non-linearity in the structure is demonstrated, as well as the sensitivity of the structure to damage of different types. The dataset is highly applicable to many academic enquiries and additional analysis techniques which will enable further advancement of vibration-based engineering techniques.

Baseline Results for Selected Nonlinear System Identification Benchmarks

Nonlinear system identification remains an important open challenge across research and academia. Large numbers of novel approaches are seen published each year, each presenting improvements or extensions to existing methods. It is natural, therefore, to consider how one might choose between these competing models. Benchmark datasets provide one clear way to approach this question. However, to make meaningful inference based on benchmark performance it is important to understand how well a new method performs comparatively to results available with well-established methods. This paper presents a set of ten baseline techniques and their relative performances on five popular benchmarks. The aim of this contribution is to stimulate thought and discussion regarding objective comparison of identification methodologies.

Probabilistic-Numeric SMC Sampling for Bayesian Nonlinear System Identification in Continuous Time

In engineering, accurately modeling nonlinear dynamic systems from data contaminated by noise is both essential and complex. Established Sequential Monte Carlo (SMC) methods, used for the Bayesian identification of these systems, facilitate the quantification of uncertainty in the parameter identification process. A significant challenge in this context is the numerical integration of continuous-time ordinary differential equations (ODEs), crucial for aligning theoretical models with discretely sampled data. This integration introduces additional numerical uncertainty, a factor that is often over looked. To address this issue, the field of probabilistic numerics combines numerical methods, such as numerical integration, with probabilistic modeling to offer a more comprehensive analysis of total uncertainty. By retaining the accuracy of classical deterministic methods, these probabilistic approaches offer a deeper understanding of the uncertainty inherent in the inference process. This paper demonstrates the application of a probabilistic numerical method for solving ODEs in the joint parameter-state identification of nonlinear dynamic systems. The presented approach efficiently identifies latent states and system parameters from noisy measurements. Simultaneously incorporating probabilistic solutions to the ODE in the identification challenge. The methodology's primary advantage lies in its capability to produce posterior distributions over system parameters, thereby representing the inherent uncertainties in both the data and the identification process.

Sharing Information Between Machine Tools to Improve Surface Finish Forecasting

At present, most surface-quality prediction methods can only perform single-task prediction which results in under-utilised datasets, repetitive work and increased experimental costs. To counter this, the authors propose a Bayesian hierarchical model to predict surface-roughness measurements for a turning machining process. The hierarchical model is compared to multiple independent Bayesian linear regression models to showcase the benefits of partial pooling in a machining setting with respect to prediction accuracy and uncertainty quantification.

A Robust Probabilistic Approach to Stochastic Subspace Identification

Modal parameter estimation of operational structures is often a challenging task when confronted with unwanted distortions (outliers) in field measurements. Atypical observations present a problem to operational modal analysis (OMA) algorithms, such as stochastic subspace identification (SSI), severely biasing parameter estimates and resulting in misidentification of the system. Despite this predicament, no simple mechanism currently exists capable of dealing with such anomalies in SSI. Addressing this problem, this paper first introduces a novel probabilistic formulation of stochastic subspace identification (Prob-SSI), realised using probabilistic projections. Mathematically, the equivalence between this model and the classic algorithm is demonstrated. This fresh perspective, viewing SSI as a problem in probabilistic inference, lays the necessary mathematical foundation to enable a plethora of new, more sophisticated OMA approaches. To this end, a statistically robust SSI algorithm (robust Prob-SSI) is developed, capable of providing a principled and automatic way of handling outlying or anomalous data in the measured timeseries, such as may occur in field recordings, e.g. intermittent sensor dropout. Robust Prob-SSI is shown to outperform conventional SSI when confronted with 'corrupted' data, exhibiting improved identification performance and higher levels of confidence in the found poles when viewing consistency (stabilisation) diagrams. Similar benefits are also demonstrated on the Z24 Bridge benchmark dataset, highlighting enhanced performance on measured systems.