Adaptive Sensor Steering Strategy Using Deep Reinforcement Learning for Dynamic Data Acquisition in Digital Twins

This paper introduces a sensor steering methodology based on deep reinforcement learning to enhance the predictive accuracy and decision support capabilities of digital twins by optimising the data acquisition process. Traditional sensor placement techniques are often constrained by one-off optimisation strategies, which limit their applicability for online applications requiring continuous informative data assimilation. The proposed approach addresses this limitation by offering an adaptive framework for sensor placement within the digital twin paradigm. The sensor placement problem is formulated as a Markov decision process, enabling the training and deployment of an agent capable of dynamically repositioning sensors in response to the evolving conditions of the physical structure as represented by the digital twin. This ensures that the digital twin maintains a highly representative and reliable connection to its physical counterpart. The proposed framework is validated through a series of comprehensive case studies involving a cantilever plate structure subjected to diverse conditions, including healthy and damaged conditions. The results demonstrate the capability of the deep reinforcement learning agent to adaptively reposition sensors improving the quality of data acquisition and hence enhancing the overall accuracy of digital twins.

Multiple-input, multiple-output modal testing of a Hawk T1A aircraft: A new full-scale dataset for structural health monitoring

The use of measured vibration data from structures has a long history of enabling the development of methods for inference and monitoring. In particular, applications based on system identification and structural health monitoring have risen to prominence over recent decades and promise significant benefits when implemented in practice. However, significant challenges remain in the development of these methods. The introduction of realistic, full-scale datasets will be an important contribution to overcoming these challenges. This paper presents a new benchmark dataset capturing the dynamic response of a decommissioned BAE Systems Hawk T1A. The dataset reflects the behaviour of a complex structure with a history of service that can still be tested in controlled laboratory conditions, using a variety of known loading and damage simulation conditions. As such, it provides a key stepping stone between simple laboratory test structures and in-service structures. In this paper, the Hawk structure is described in detail, alongside a comprehensive summary of the experimental work undertaken. Following this, key descriptive highlights of the dataset are presented, before a discussion of the research challenges that the data present. Using the dataset, non-linearity in the structure is demonstrated, as well as the sensitivity of the structure to damage of different types. The dataset is highly applicable to many academic enquiries and additional analysis techniques which will enable further advancement of vibration-based engineering techniques.

Foundations of Population-Based SHM, Part IV: The Geometry of Spaces of Structures and their Feature Spaces

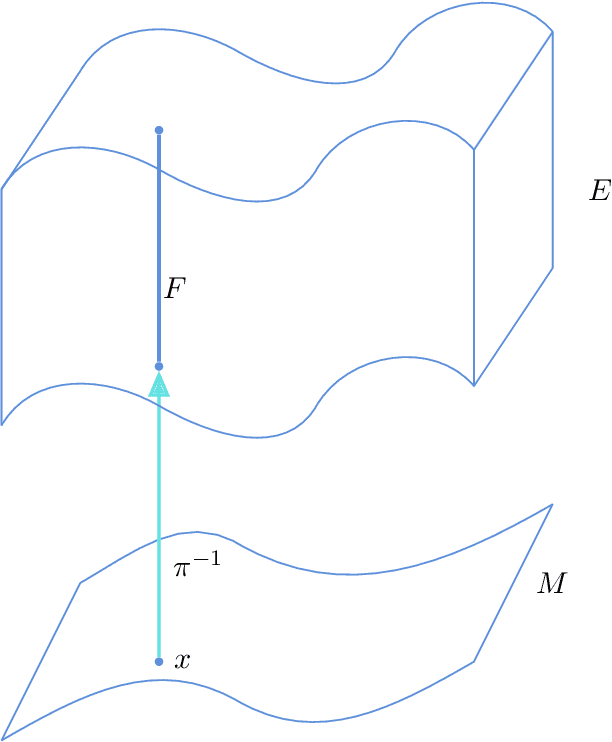
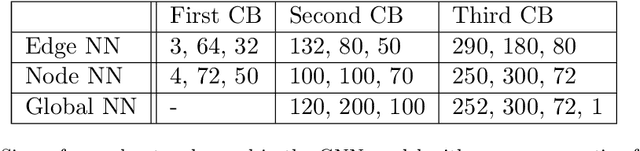
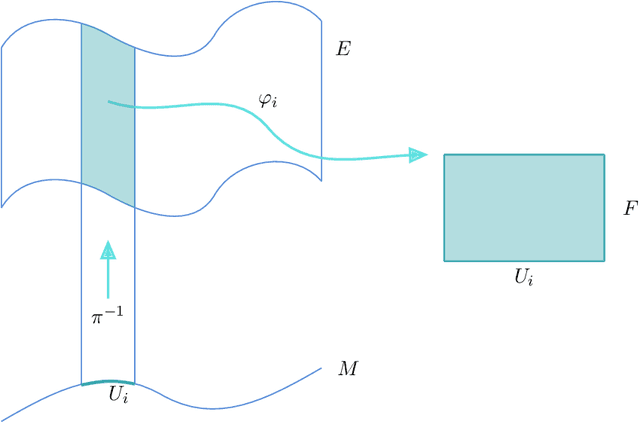
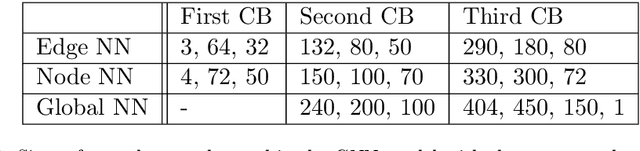
One of the requirements of the population-based approach to Structural Health Monitoring (SHM) proposed in the earlier papers in this sequence, is that structures be represented by points in an abstract space. Furthermore, these spaces should be metric spaces in a loose sense; i.e. there should be some measure of distance applicable to pairs of points; similar structures should then be close in the metric. However, this geometrical construction is not enough for the framing of problems in data-based SHM, as it leaves undefined the notion of feature spaces. Interpreting the feature values on a structure-by-structure basis as a type of field over the space of structures, it seems sensible to borrow an idea from modern theoretical physics, and define feature assignments as sections in a vector bundle over the structure space. With this idea in place, one can interpret the effect of environmental and operational variations as gauge degrees of freedom, as in modern gauge field theories. This paper will discuss the various geometrical structures required for an abstract theory of feature spaces in SHM, and will draw analogies with how these structures have shown their power in modern physics. In the second part of the paper, the problem of determining the normal condition cross section of a feature bundle is addressed. The solution is provided by the application of Graph Neural Networks (GNN), a versatile non-Euclidean machine learning algorithm which is not restricted to inputs and outputs from vector spaces. In particular, the algorithm is well suited to operating directly on the sort of graph structures which are an important part of the proposed framework for PBSHM. The solution of the normal section problem is demonstrated for a heterogeneous population of truss structures for which the feature of interest is the first natural frequency.