Towards an active-learning approach to resource allocation for population-based damage prognosis

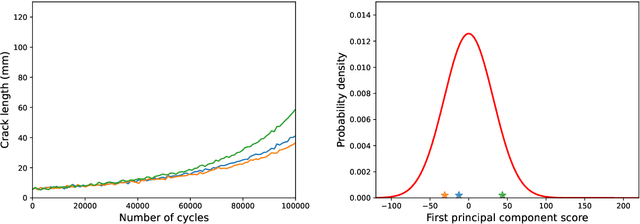
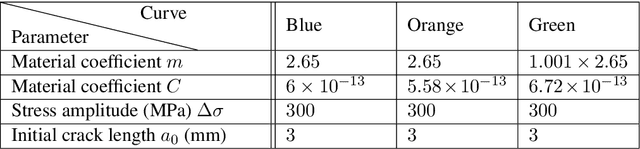
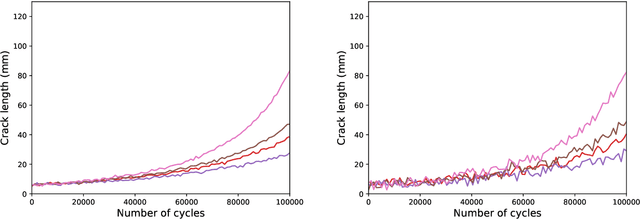
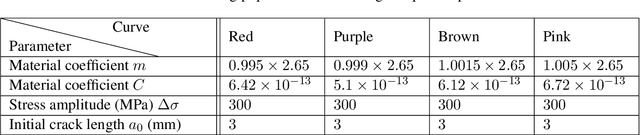
Damage prognosis is, arguably, one of the most difficult tasks of structural health monitoring (SHM). To address common problems of damage prognosis, a population-based SHM (PBSHM) approach is adopted in the current work. In this approach the prognosis problem is considered as an information-sharing problem where data from past structures are exploited to make more accurate inferences regarding currently-degrading structures. For a given population, there may exist restrictions on the resources available to conduct monitoring; thus, the current work studies the problem of allocating such resources within a population of degrading structures with a view to maximising the damage-prognosis accuracy. The challenges of the current framework are mainly associated with the inference of outliers on the level of damage evolution, given partial data from the damage-evolution phenomenon. The current approach considers an initial population of structures for which damage evolution is extensively observed. Subsequently, a second population of structures with evolving damage is considered for which two monitoring systems are available, a low-availability and high-fidelity (low-uncertainty) one, and a widely-available and low-fidelity (high-uncertainty) one. The task of the current work is to follow an active-learning approach to identify the structures to which the high-fidelity system should be assigned in order to enhance the predictive capabilities of the machine-learning model throughout the population.

Foundations of Population-Based SHM, Part IV: The Geometry of Spaces of Structures and their Feature Spaces

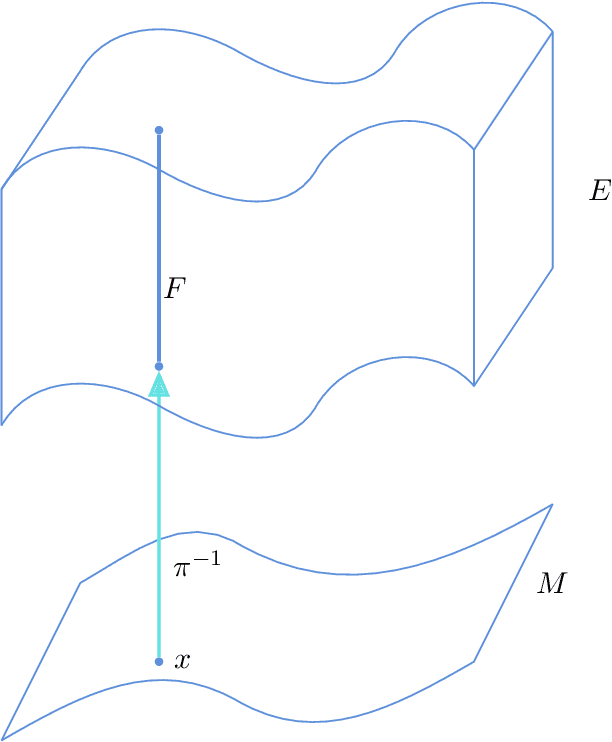
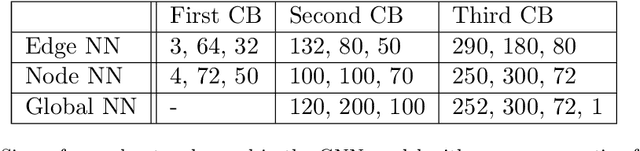
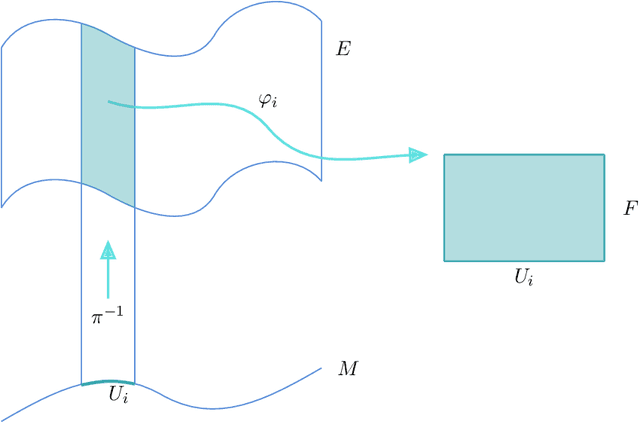
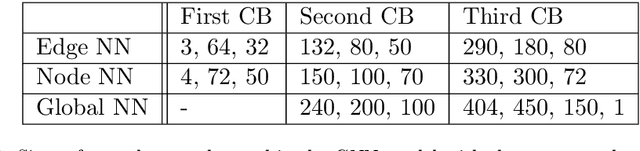
One of the requirements of the population-based approach to Structural Health Monitoring (SHM) proposed in the earlier papers in this sequence, is that structures be represented by points in an abstract space. Furthermore, these spaces should be metric spaces in a loose sense; i.e. there should be some measure of distance applicable to pairs of points; similar structures should then be close in the metric. However, this geometrical construction is not enough for the framing of problems in data-based SHM, as it leaves undefined the notion of feature spaces. Interpreting the feature values on a structure-by-structure basis as a type of field over the space of structures, it seems sensible to borrow an idea from modern theoretical physics, and define feature assignments as sections in a vector bundle over the structure space. With this idea in place, one can interpret the effect of environmental and operational variations as gauge degrees of freedom, as in modern gauge field theories. This paper will discuss the various geometrical structures required for an abstract theory of feature spaces in SHM, and will draw analogies with how these structures have shown their power in modern physics. In the second part of the paper, the problem of determining the normal condition cross section of a feature bundle is addressed. The solution is provided by the application of Graph Neural Networks (GNN), a versatile non-Euclidean machine learning algorithm which is not restricted to inputs and outputs from vector spaces. In particular, the algorithm is well suited to operating directly on the sort of graph structures which are an important part of the proposed framework for PBSHM. The solution of the normal section problem is demonstrated for a heterogeneous population of truss structures for which the feature of interest is the first natural frequency.