Port-Hamiltonian Neural Networks with Output Error Noise Models

Hamiltonian neural networks (HNNs) represent a promising class of physics-informed deep learning methods that utilize Hamiltonian theory as foundational knowledge within neural networks. However, their direct application to engineering systems is often challenged by practical issues, including the presence of external inputs, dissipation, and noisy measurements. This paper introduces a novel framework that enhances the capabilities of HNNs to address these real-life factors. We integrate port-Hamiltonian theory into the neural network structure, allowing for the inclusion of external inputs and dissipation, while mitigating the impact of measurement noise through an output-error (OE) model structure. The resulting output error port-Hamiltonian neural networks (OE-pHNNs) can be adapted to tackle modeling complex engineering systems with noisy measurements. Furthermore, we propose the identification of OE-pHNNs based on the subspace encoder approach (SUBNET), which efficiently approximates the complete simulation loss using subsections of the data and uses an encoder function to predict initial states. By integrating SUBNET with OE-pHNNs, we achieve consistent models of complex engineering systems under noisy measurements. In addition, we perform a consistency analysis to ensure the reliability of the proposed data-driven model learning method. We demonstrate the effectiveness of our approach on system identification benchmarks, showing its potential as a powerful tool for modeling dynamic systems in real-world applications.

Physics-Informed Learning Using Hamiltonian Neural Networks with Output Error Noise Models

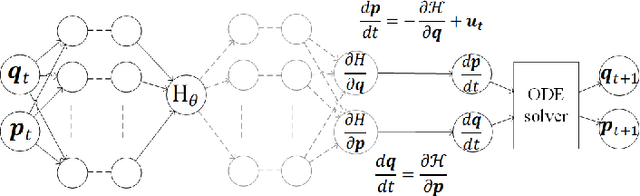
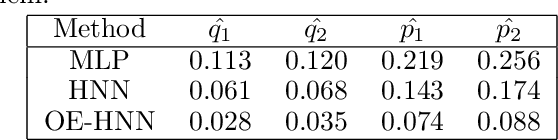
In order to make data-driven models of physical systems interpretable and reliable, it is essential to include prior physical knowledge in the modeling framework. Hamiltonian Neural Networks (HNNs) implement Hamiltonian theory in deep learning and form a comprehensive framework for modeling autonomous energy-conservative systems. Despite being suitable to estimate a wide range of physical system behavior from data, classical HNNs are restricted to systems without inputs and require noiseless state measurements and information on the derivative of the state to be available. To address these challenges, this paper introduces an Output Error Hamiltonian Neural Network (OE-HNN) modeling approach to address the modeling of physical systems with inputs and noisy state measurements. Furthermore, it does not require the state derivatives to be known. Instead, the OE-HNN utilizes an ODE-solver embedded in the training process, which enables the OE-HNN to learn the dynamics from noisy state measurements. In addition, extending HNNs based on the generalized Hamiltonian theory enables to include external inputs into the framework which are important for engineering applications. We demonstrate via simulation examples that the proposed OE-HNNs results in superior modeling performance compared to classical HNNs.