CarMem: Enhancing Long-Term Memory in LLM Voice Assistants through Category-Bounding

In today's assistant landscape, personalisation enhances interactions, fosters long-term relationships, and deepens engagement. However, many systems struggle with retaining user preferences, leading to repetitive user requests and disengagement. Furthermore, the unregulated and opaque extraction of user preferences in industry applications raises significant concerns about privacy and trust, especially in regions with stringent regulations like Europe. In response to these challenges, we propose a long-term memory system for voice assistants, structured around predefined categories. This approach leverages Large Language Models to efficiently extract, store, and retrieve preferences within these categories, ensuring both personalisation and transparency. We also introduce a synthetic multi-turn, multi-session conversation dataset (CarMem), grounded in real industry data, tailored to an in-car voice assistant setting. Benchmarked on the dataset, our system achieves an F1-score of .78 to .95 in preference extraction, depending on category granularity. Our maintenance strategy reduces redundant preferences by 95% and contradictory ones by 92%, while the accuracy of optimal retrieval is at .87. Collectively, the results demonstrate the system's suitability for industrial applications.

Learning the Koopman Eigendecomposition: A Diffeomorphic Approach

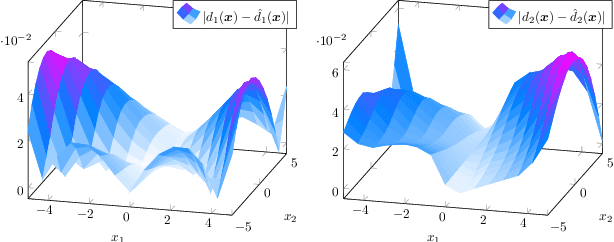
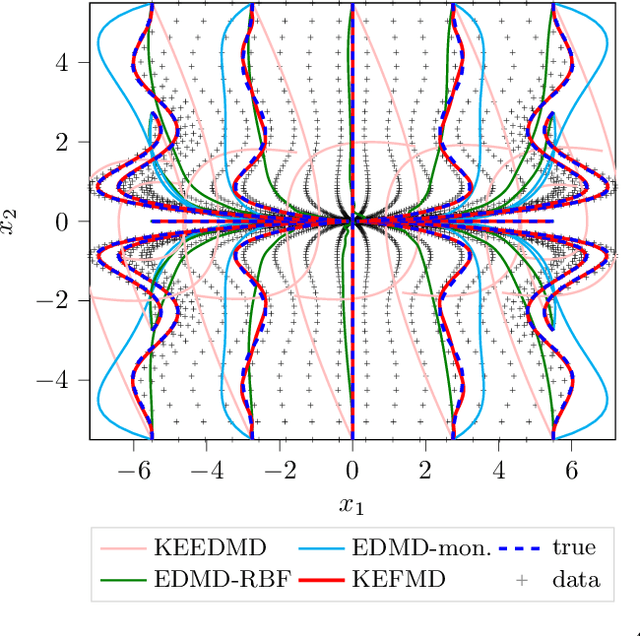
We present a novel data-driven approach for learning linear representations of a class of stable nonlinear systems using Koopman eigenfunctions. By learning the conjugacy map between a nonlinear system and its Jacobian linearization through a Normalizing Flow one can guarantee the learned function is a diffeomorphism. Using this diffeomorphism, we construct eigenfunctions of the nonlinear system via the spectral equivalence of conjugate systems - allowing the construction of linear predictors for nonlinear systems. The universality of the diffeomorphism learner leads to the universal approximation of the nonlinear system's Koopman eigenfunctions. The developed method is also safe as it guarantees the model is asymptotically stable regardless of the representation accuracy. To our best knowledge, this is the first work to close the gap between the operator, system and learning theories. The efficacy of our approach is shown through simulation examples.