Jana Janeva
Linear-Time Contact and Friction Dynamics in Maximal Coordinates using Variational Integrators
Sep 15, 2021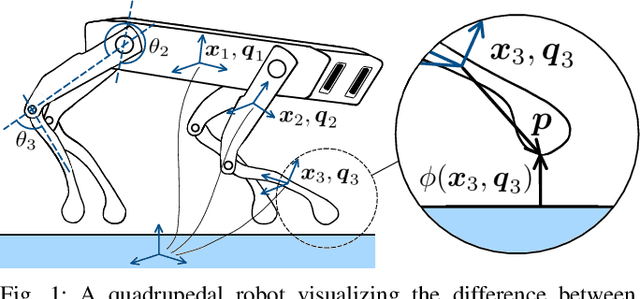
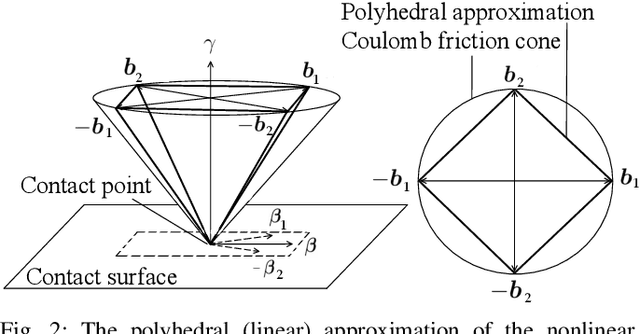
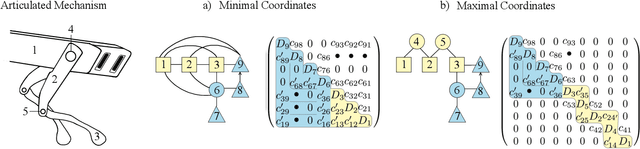
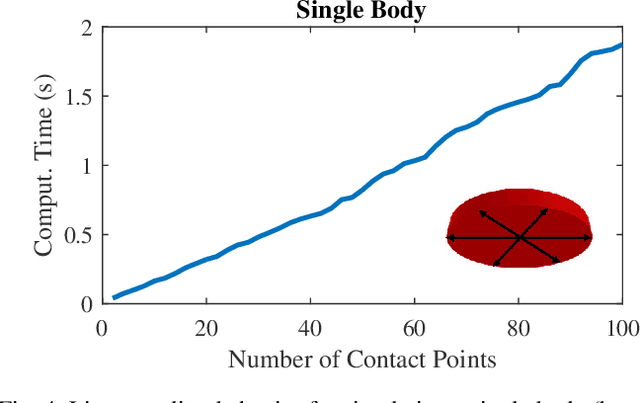
Abstract:Simulation of contact and friction dynamics is an important basis for control- and learning-based algorithms. However, the numerical difficulties of contact interactions pose a challenge for robust and efficient simulators. A maximal-coordinate representation of the dynamics enables efficient solving algorithms, but current methods in maximal coordinates require constraint stabilization schemes. Therefore, we propose an interior-point algorithm for the numerically robust treatment of rigid-body dynamics with contact interactions in maximal coordinates. Additionally, we discretize the dynamics with a variational integrator to prevent constraint drift. Our algorithm achieves linear-time complexity both in the number of contact points and the number of bodies, which is shown theoretically and demonstrated with an implementation. Furthermore, we simulate two robotic systems to highlight the applicability of the proposed algorithm.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge