Learning Safe Control via On-the-Fly Bandit Exploration

Control tasks with safety requirements under high levels of model uncertainty are increasingly common. Machine learning techniques are frequently used to address such tasks, typically by leveraging model error bounds to specify robust constraint-based safety filters. However, if the learned model uncertainty is very high, the corresponding filters are potentially invalid, meaning no control input satisfies the constraints imposed by the safety filter. While most works address this issue by assuming some form of safe backup controller, ours tackles it by collecting additional data on the fly using a Gaussian process bandit-type algorithm. We combine a control barrier function with a learned model to specify a robust certificate that ensures safety if feasible. Whenever infeasibility occurs, we leverage the control barrier function to guide exploration, ensuring the collected data contributes toward the closed-loop system safety. By combining a safety filter with exploration in this manner, our method provably achieves safety in a setting that allows for a zero-mean prior dynamics model, without requiring a backup controller. To the best of our knowledge, it is the first safe learning-based control method that achieves this.

Safe Online Dynamics Learning with Initially Unknown Models and Infeasible Safety Certificates

Safety-critical control tasks with high levels of uncertainty are becoming increasingly common. Typically, techniques that guarantee safety during learning and control utilize constraint-based safety certificates, which can be leveraged to compute safe control inputs. However, excessive model uncertainty can render robust safety certification methods or infeasible, meaning no control input satisfies the constraints imposed by the safety certificate. This paper considers a learning-based setting with a robust safety certificate based on a control barrier function (CBF) second-order cone program. If the control barrier function certificate is feasible, our approach leverages it to guarantee safety. Otherwise, our method explores the system dynamics to collect data and recover the feasibility of the control barrier function constraint. To this end, we employ a method inspired by well-established tools from Bayesian optimization. We show that if the sampling frequency is high enough, we recover the feasibility of the robust CBF certificate, guaranteeing safety. Our approach requires no prior model and corresponds, to the best of our knowledge, to the first algorithm that guarantees safety in settings with occasionally infeasible safety certificates without requiring a backup non-learning-based controller.

Receding Horizon Planning with Rule Hierarchies for Autonomous Vehicles

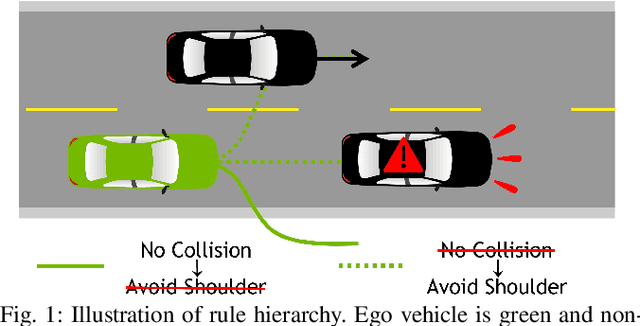
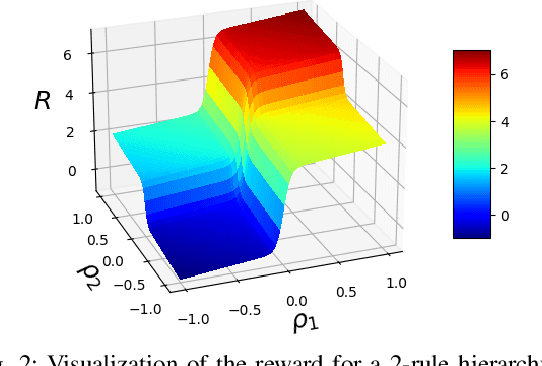
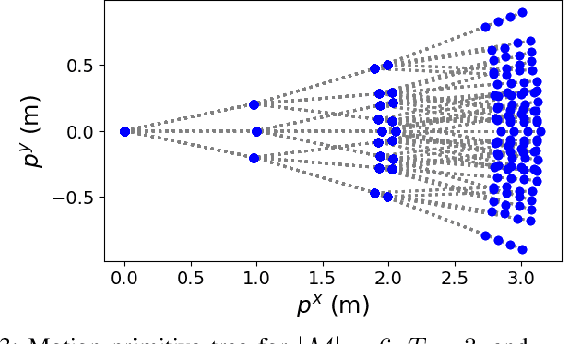
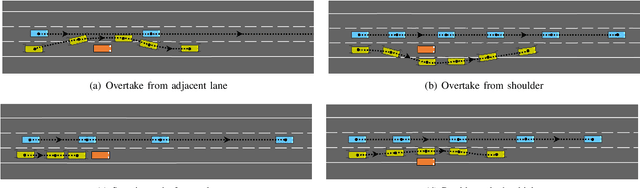
Autonomous vehicles must often contend with conflicting planning requirements, e.g., safety and comfort could be at odds with each other if avoiding a collision calls for slamming the brakes. To resolve such conflicts, assigning importance ranking to rules (i.e., imposing a rule hierarchy) has been proposed, which, in turn, induces rankings on trajectories based on the importance of the rules they satisfy. On one hand, imposing rule hierarchies can enhance interpretability, but introduce combinatorial complexity to planning; while on the other hand, differentiable reward structures can be leveraged by modern gradient-based optimization tools, but are less interpretable and unintuitive to tune. In this paper, we present an approach to equivalently express rule hierarchies as differentiable reward structures amenable to modern gradient-based optimizers, thereby, achieving the best of both worlds. We achieve this by formulating rank-preserving reward functions that are monotonic in the rank of the trajectories induced by the rule hierarchy; i.e., higher ranked trajectories receive higher reward. Equipped with a rule hierarchy and its corresponding rank-preserving reward function, we develop a two-stage planner that can efficiently resolve conflicting planning requirements. We demonstrate that our approach can generate motion plans in ~7-10 Hz for various challenging road navigation and intersection negotiation scenarios.