Robust Locomotion on Legged Robots through Planning on Motion Primitive Graphs
Paper and Code
Sep 15, 2022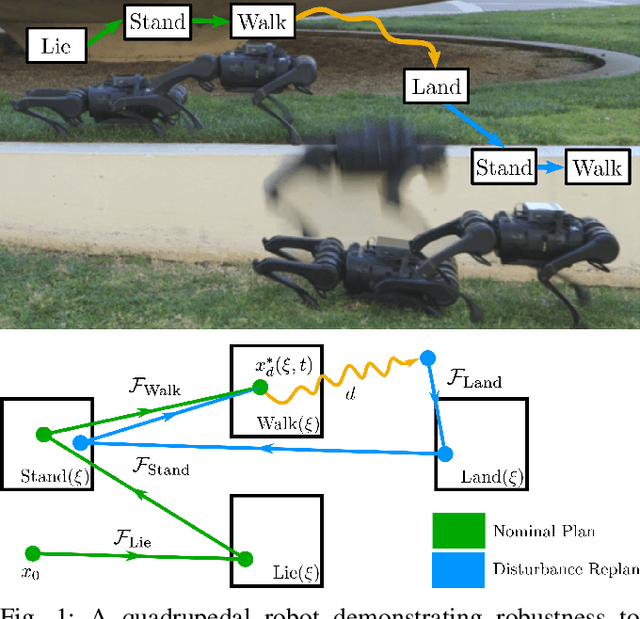
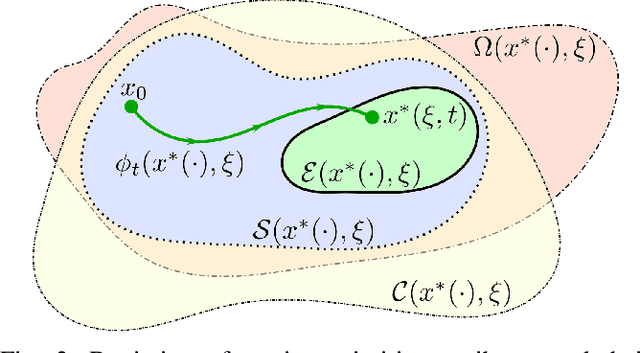
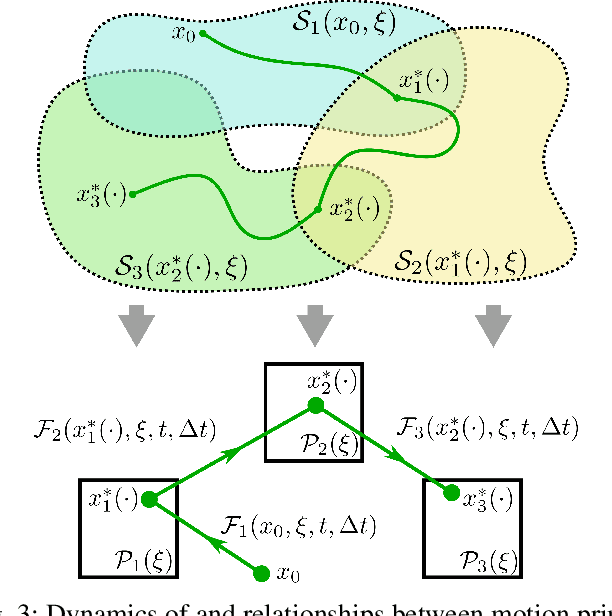
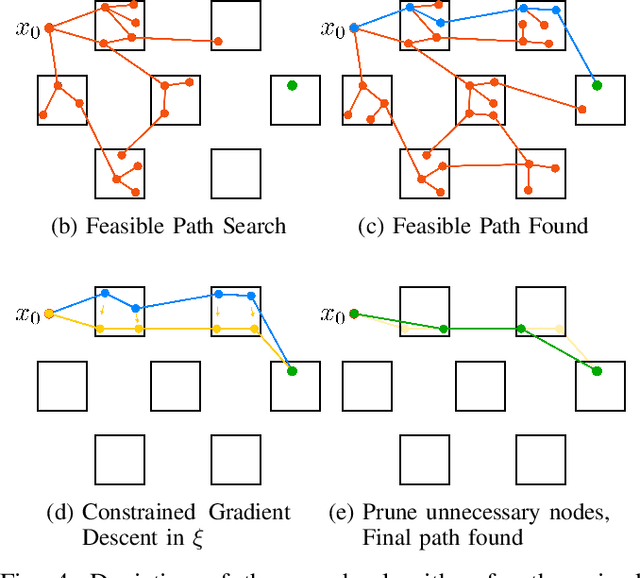
The functional demands of robotic systems often require completing various tasks or behaviors under the effect of disturbances or uncertain environments. Of increasing interest is the autonomy for dynamic robots, such as multirotors, motor vehicles, and legged platforms. Here, disturbances and environmental conditions can have significant impact on the successful performance of the individual dynamic behaviors, referred to as "motion primitives". Despite this, robustness can be achieved by switching to and transitioning through suitable motion primitives. This paper contributes such a method by presenting an abstraction of the motion primitive dynamics and a corresponding "motion primitive transfer function". From this, a mixed discrete and continuous "motion primitive graph" is constructed, and an algorithm capable of online search of this graph is detailed. The result is a framework capable of realizing holistic robustness on dynamic systems. This is experimentally demonstrated for a set of motion primitives on a quadrupedal robot, subject to various environmental and intentional disturbances.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge