Risk-Aware Robotics: Tail Risk Measures in Planning, Control, and Verification

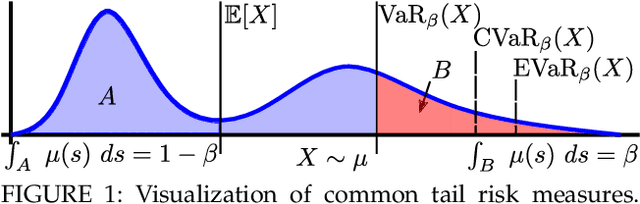
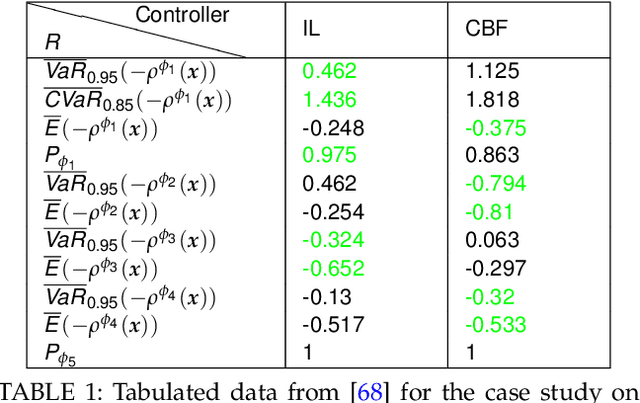
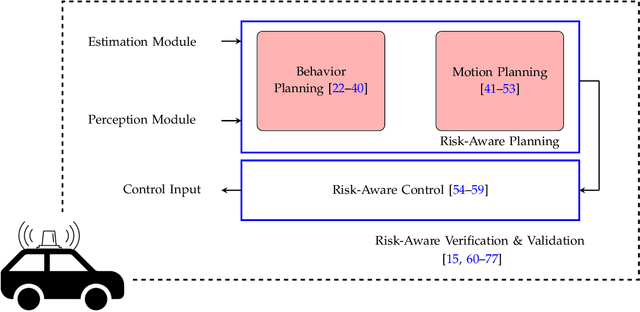
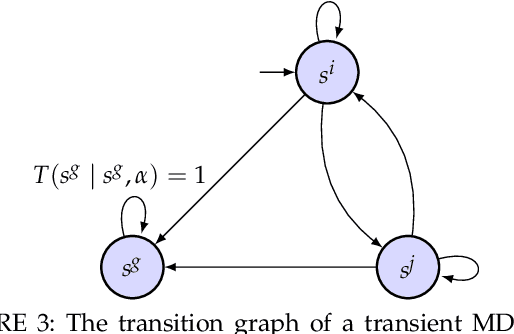
The need for a systematic approach to risk assessment has increased in recent years due to the ubiquity of autonomous systems that alter our day-to-day experiences and their need for safety, e.g., for self-driving vehicles, mobile service robots, and bipedal robots. These systems are expected to function safely in unpredictable environments and interact seamlessly with humans, whose behavior is notably challenging to forecast. We present a survey of risk-aware methodologies for autonomous systems. We adopt a contemporary risk-aware approach to mitigate rare and detrimental outcomes by advocating the use of tail risk measures, a concept borrowed from financial literature. This survey will introduce these measures and explain their relevance in the context of robotic systems for planning, control, and verification applications.

Barrier-Based Test Synthesis for Safety-Critical Systems Subject to Timed Reach-Avoid Specifications

We propose an adversarial, time-varying test-synthesis procedure for safety-critical systems without requiring specific knowledge of the underlying controller steering the system. From a broader test and evaluation context, determination of difficult tests of system behavior is important as these tests would elucidate problematic system phenomena before these mistakes can engender problematic outcomes, e.g. loss of human life in autonomous cars, costly failures for airplane systems, etc. Our approach builds on existing, simulation-based work in the test and evaluation literature by offering a controller-agnostic test-synthesis procedure that provides a series of benchmark tests with which to determine controller reliability. To achieve this, our approach codifies the system objective as a timed reach-avoid specification. Then, by coupling control barrier functions with this class of specifications, we construct an instantaneous difficulty metric whose minimizer corresponds to the most difficult test at that system state. We use this instantaneous difficulty metric in a game-theoretic fashion, to produce an adversarial, time-varying test-synthesis procedure that does not require specific knowledge of the system's controller, but can still provably identify realizable and maximally difficult tests of system behavior. Finally, we develop this test-synthesis procedure for both continuous and discrete-time systems and showcase our test-synthesis procedure on simulated and hardware examples.

Sample-Based Bounds for Coherent Risk Measures: Applications to Policy Synthesis and Verification

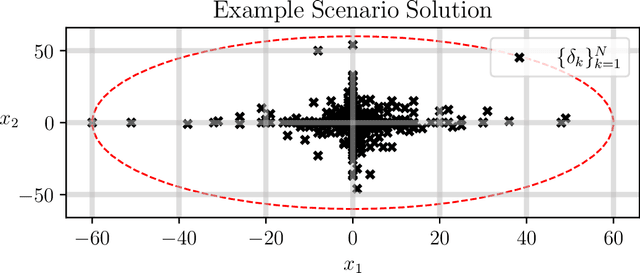
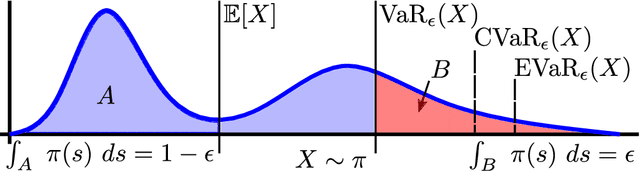
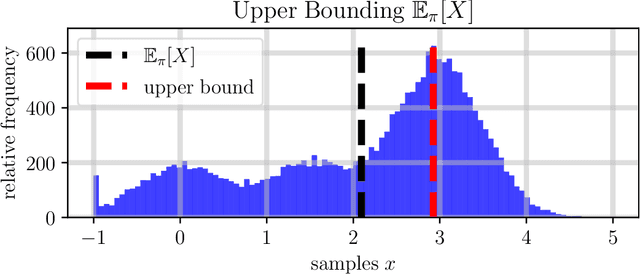
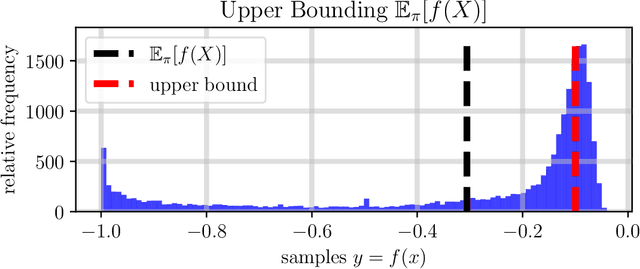
The dramatic increase of autonomous systems subject to variable environments has given rise to the pressing need to consider risk in both the synthesis and verification of policies for these systems. This paper aims to address a few problems regarding risk-aware verification and policy synthesis, by first developing a sample-based method to bound the risk measure evaluation of a random variable whose distribution is unknown. These bounds permit us to generate high-confidence verification statements for a large class of robotic systems. Second, we develop a sample-based method to determine solutions to non-convex optimization problems that outperform a large fraction of the decision space of possible solutions. Both sample-based approaches then permit us to rapidly synthesize risk-aware policies that are guaranteed to achieve a minimum level of system performance. To showcase our approach in simulation, we verify a cooperative multi-agent system and develop a risk-aware controller that outperforms the system's baseline controller. We also mention how our approach can be extended to account for any $g$-entropic risk measure - the subset of coherent risk measures on which we focus.

Risk-Averse Receding Horizon Motion Planning

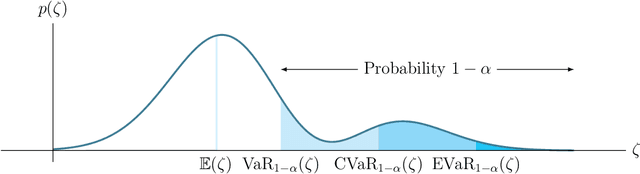
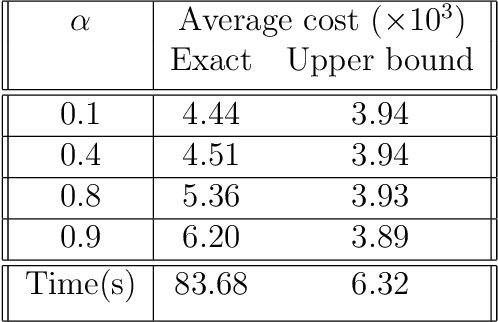
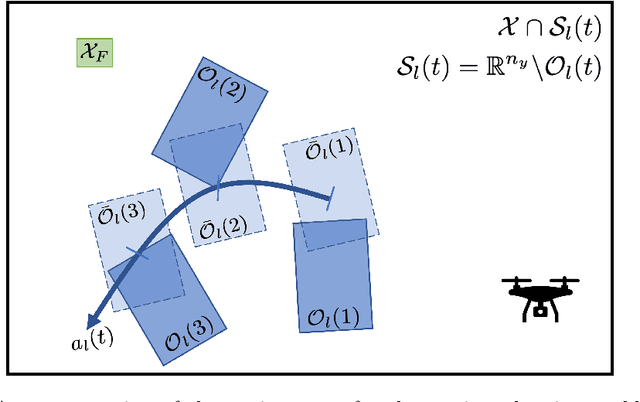
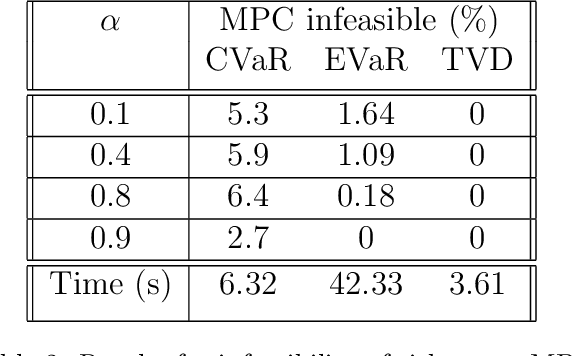
This paper studies the problem of risk-averse receding horizon motion planning for agents with uncertain dynamics, in the presence of stochastic, dynamic obstacles. We propose a model predictive control (MPC) scheme that formulates the obstacle avoidance constraint using coherent risk measures. To handle disturbances, or process noise, in the state dynamics, the state constraints are tightened in a risk-aware manner to provide a disturbance feedback policy. We also propose a waypoint following algorithm that uses the proposed MPC scheme for discrete distributions and prove its risk-sensitive recursive feasibility while guaranteeing finite-time task completion. We further investigate some commonly used coherent risk metrics, namely, conditional value-at-risk (CVaR), entropic value-at-risk (EVaR), and g-entropic risk measures, and propose a tractable incorporation within MPC. We illustrate our framework via simulation studies.

Distributionally Robust Model Predictive Control with Total Variation Distance

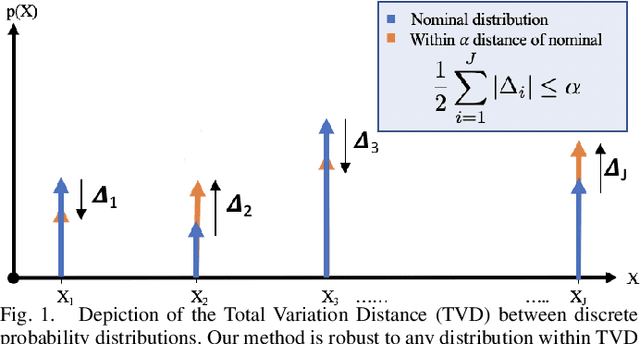
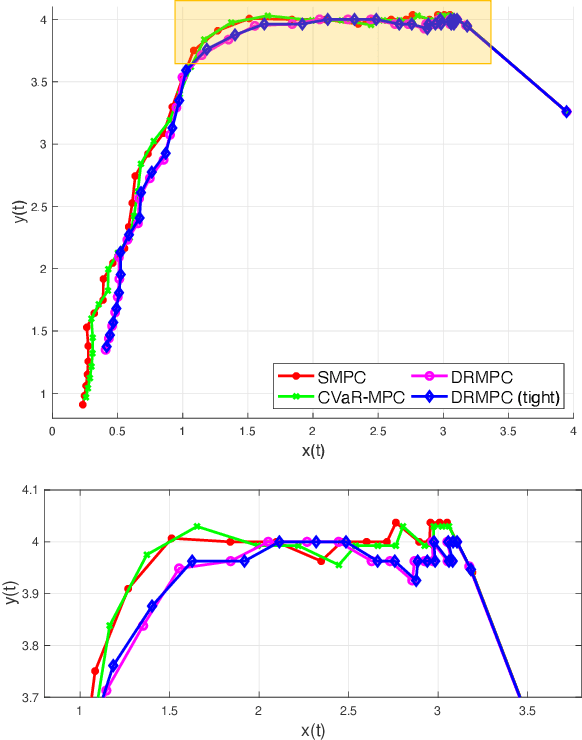
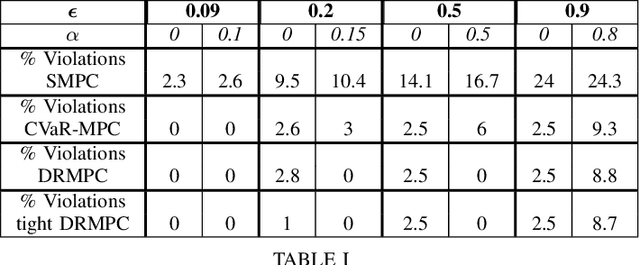
This paper studies the problem of distributionally robust model predictive control (MPC) using total variation distance ambiguity sets. For a discrete-time linear system with additive disturbances, we provide a conditional value-at-risk reformulation of the MPC optimization problem that is distributionally robust in the expected cost and chance constraints. The distributionally robust chance constraint is over-approximated as a tightened chance constraint, wherein the tightening for each time step in the MPC can be computed offline, hence reducing the computational burden. We conclude with numerical experiments to support our results on the probabilistic guarantees and computational efficiency.

Risk-Averse Decision Making Under Uncertainty

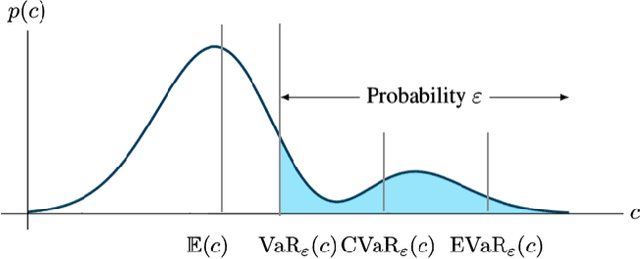
A large class of decision making under uncertainty problems can be described via Markov decision processes (MDPs) or partially observable MDPs (POMDPs), with application to artificial intelligence and operations research, among others. Traditionally, policy synthesis techniques are proposed such that a total expected cost or reward is minimized or maximized. However, optimality in the total expected cost sense is only reasonable if system behavior in the large number of runs is of interest, which has limited the use of such policies in practical mission-critical scenarios, wherein large deviations from the expected behavior may lead to mission failure. In this paper, we consider the problem of designing policies for MDPs and POMDPs with objectives and constraints in terms of dynamic coherent risk measures, which we refer to as the constrained risk-averse problem. For MDPs, we reformulate the problem into a infsup problem via the Lagrangian framework and propose an optimization-based method to synthesize Markovian policies. For MDPs, we demonstrate that the formulated optimization problems are in the form of difference convex programs (DCPs) and can be solved by the disciplined convex-concave programming (DCCP) framework. We show that these results generalize linear programs for constrained MDPs with total discounted expected costs and constraints. For POMDPs, we show that, if the coherent risk measures can be defined as a Markov risk transition mapping, an infinite-dimensional optimization can be used to design Markovian belief-based policies. For stochastic finite-state controllers (FSCs), we show that the latter optimization simplifies to a (finite-dimensional) DCP and can be solved by the DCCP framework. We incorporate these DCPs in a policy iteration algorithm to design risk-averse FSCs for POMDPs.

Risk-Averse Stochastic Shortest Path Planning

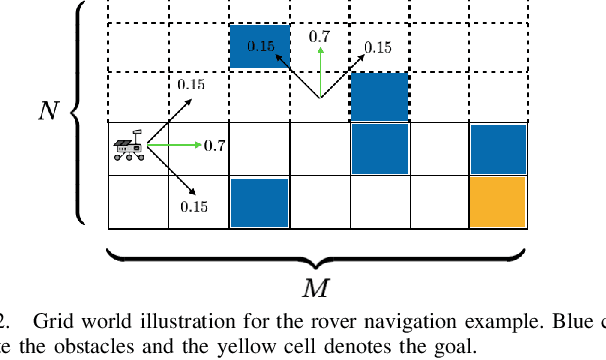
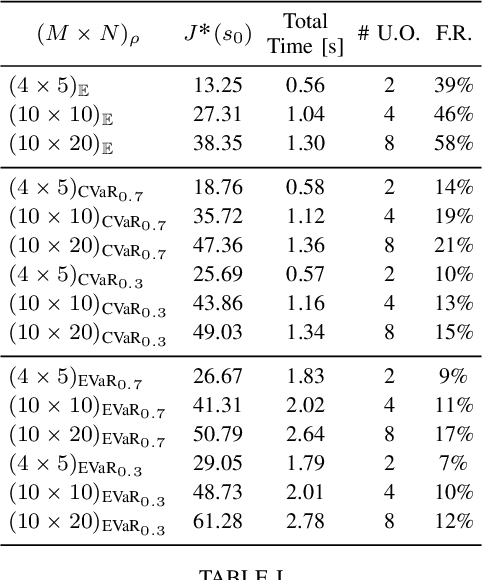
We consider the stochastic shortest path planning problem in MDPs, i.e., the problem of designing policies that ensure reaching a goal state from a given initial state with minimum accrued cost. In order to account for rare but important realizations of the system, we consider a nested dynamic coherent risk total cost functional rather than the conventional risk-neutral total expected cost. Under some assumptions, we show that optimal, stationary, Markovian policies exist and can be found via a special Bellman's equation. We propose a computational technique based on difference convex programs (DCPs) to find the associated value functions and therefore the risk-averse policies. A rover navigation MDP is used to illustrate the proposed methodology with conditional-value-at-risk (CVaR) and entropic-value-at-risk (EVaR) coherent risk measures.

Constrained Risk-Averse Markov Decision Processes

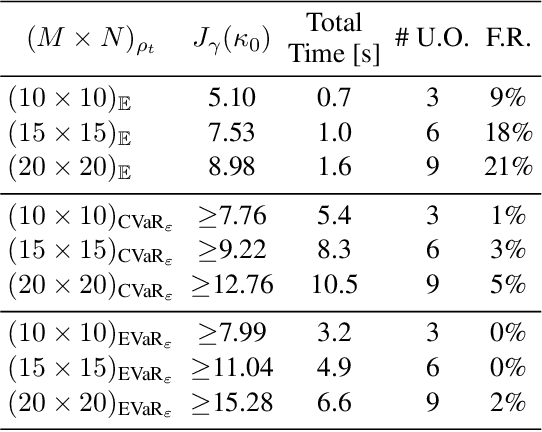
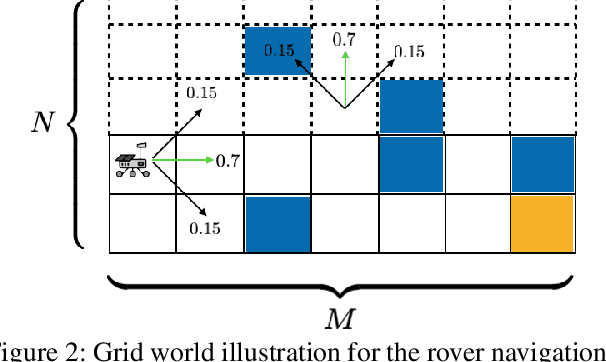
We consider the problem of designing policies for Markov decision processes (MDPs) with dynamic coherent risk objectives and constraints. We begin by formulating the problem in a Lagrangian framework. Under the assumption that the risk objectives and constraints can be represented by a Markov risk transition mapping, we propose an optimization-based method to synthesize Markovian policies that lower-bound the constrained risk-averse problem. We demonstrate that the formulated optimization problems are in the form of difference convex programs (DCPs) and can be solved by the disciplined convex-concave programming (DCCP) framework. We show that these results generalize linear programs for constrained MDPs with total discounted expected costs and constraints. Finally, we illustrate the effectiveness of the proposed method with numerical experiments on a rover navigation problem involving conditional-value-at-risk (CVaR) and entropic-value-at-risk (EVaR) coherent risk measures.

Risk-Sensitive Motion Planning using Entropic Value-at-Risk

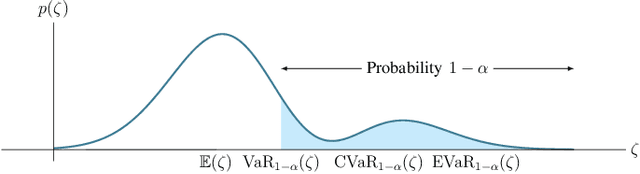
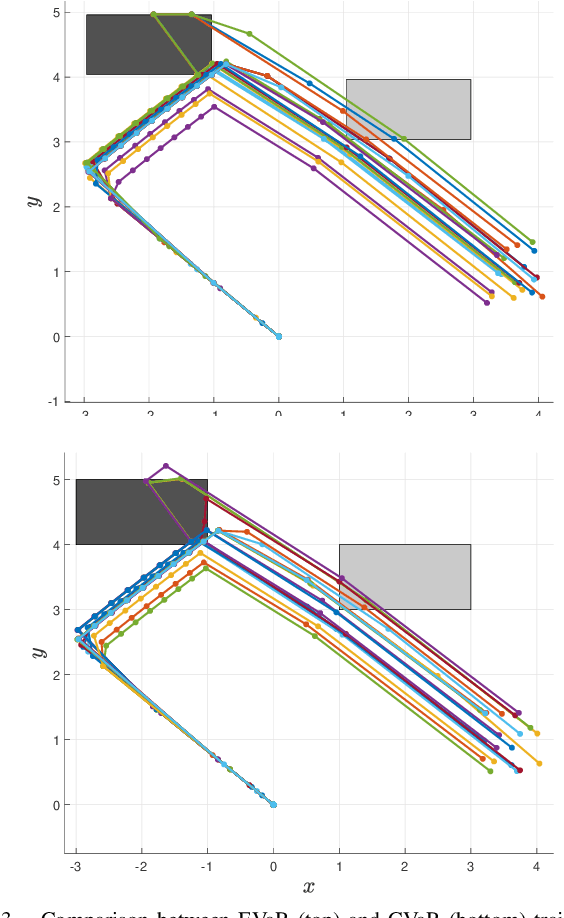
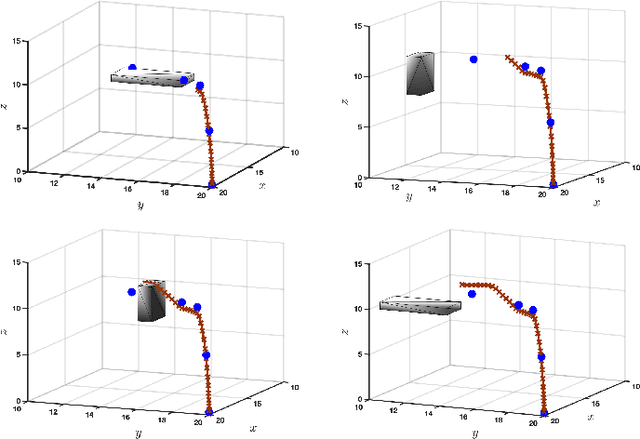
We consider the problem of risk-sensitive motion planning in the presence of randomly moving obstacles. To this end, we adopt a model predictive control (MPC) scheme and pose the obstacle avoidance constraint in the MPC problem as a distributionally robust constraint with a KL divergence ambiguity set. This constraint is the dual representation of the Entropic Value-at-Risk (EVaR). Building upon this viewpoint, we propose an algorithm to follow waypoints and discuss its feasibility and completion in finite time. We compare the policies obtained using EVaR with those obtained using another common coherent risk measure, Conditional Value-at-Risk (CVaR), via numerical experiments for a 2D system. We also implement the waypoint following algorithm on a 3D quadcopter simulation.

Risk-Sensitive Path Planning via CVaR Barrier Functions: Application to Bipedal Locomotion

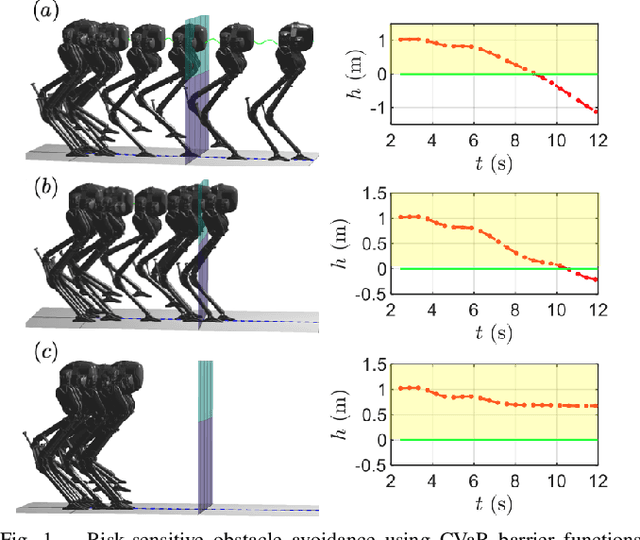
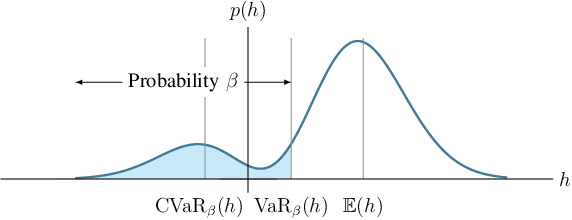
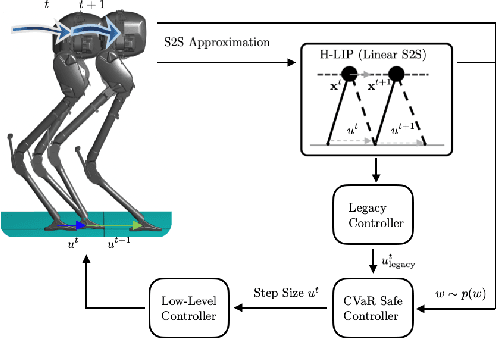
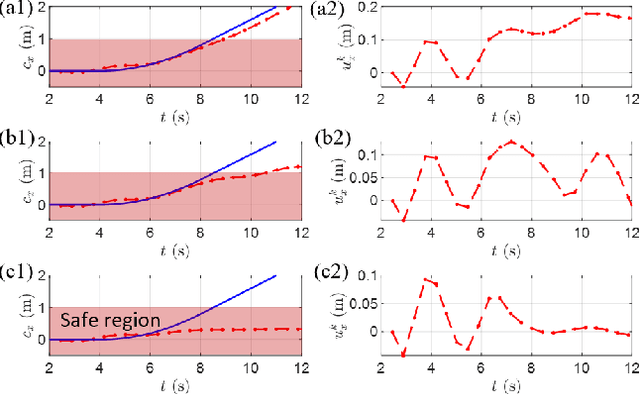
Enforcing safety of robotic systems in the presence of stochastic uncertainty is a challenging problem. Traditionally,researchers have proposed safety in the statistical mean as a safety measure in this case. However, ensuring safety in the statistical mean is only reasonable if robot safe behavior in the large number of runs is of interest, which precludes the use of mean safety in practical scenarios. In this paper, we propose a risk sensitive notion of safety called conditional-value-at-risk (CVaR) safety, which is concerned with safe performance in the worst case realizations. We introduce CVaR barrier functions asa tool to enforce CVaR safety and propose conditions for their Boolean compositions. Given a legacy controller, we show that we can design a minimally interfering CVaR safe controller via solving difference convex programs. We elucidate the proposed method by applying it to a bipedal locomotion case study.