Risk-Averse Stochastic Shortest Path Planning
Paper and Code
Mar 26, 2021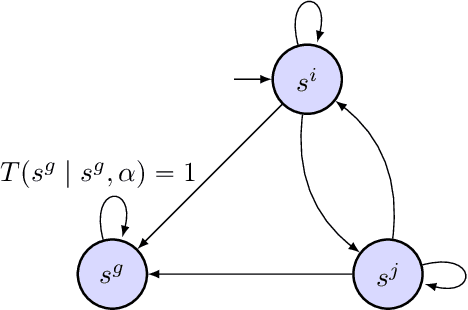
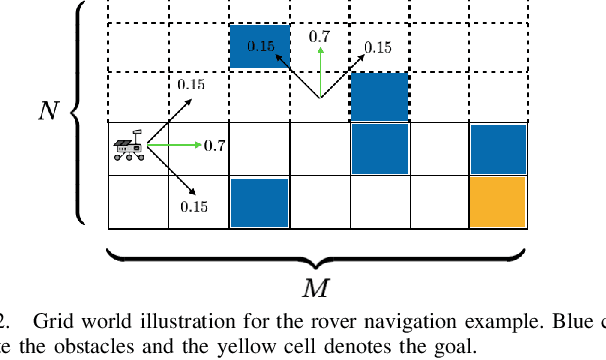
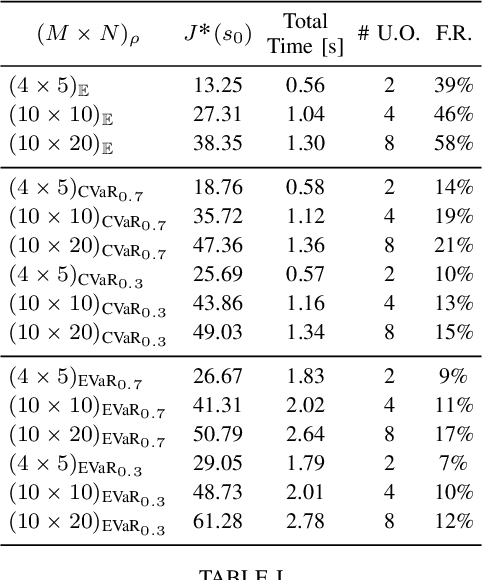
We consider the stochastic shortest path planning problem in MDPs, i.e., the problem of designing policies that ensure reaching a goal state from a given initial state with minimum accrued cost. In order to account for rare but important realizations of the system, we consider a nested dynamic coherent risk total cost functional rather than the conventional risk-neutral total expected cost. Under some assumptions, we show that optimal, stationary, Markovian policies exist and can be found via a special Bellman's equation. We propose a computational technique based on difference convex programs (DCPs) to find the associated value functions and therefore the risk-averse policies. A rover navigation MDP is used to illustrate the proposed methodology with conditional-value-at-risk (CVaR) and entropic-value-at-risk (EVaR) coherent risk measures.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge