Distributionally Robust Model Predictive Control with Total Variation Distance

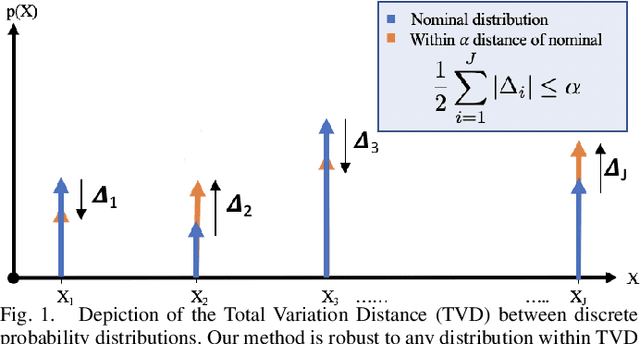
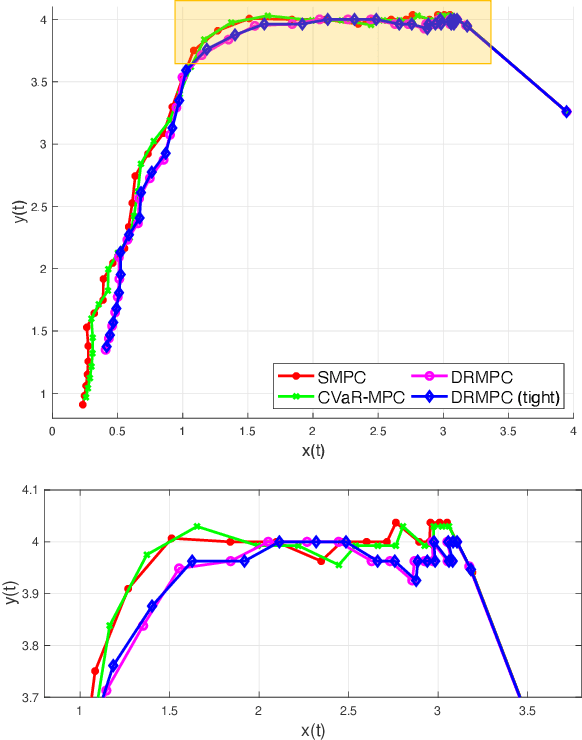
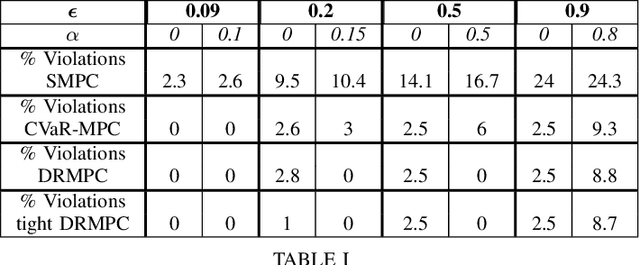
This paper studies the problem of distributionally robust model predictive control (MPC) using total variation distance ambiguity sets. For a discrete-time linear system with additive disturbances, we provide a conditional value-at-risk reformulation of the MPC optimization problem that is distributionally robust in the expected cost and chance constraints. The distributionally robust chance constraint is over-approximated as a tightened chance constraint, wherein the tightening for each time step in the MPC can be computed offline, hence reducing the computational burden. We conclude with numerical experiments to support our results on the probabilistic guarantees and computational efficiency.