Risk-Sensitive Motion Planning using Entropic Value-at-Risk
Paper and Code
Nov 23, 2020
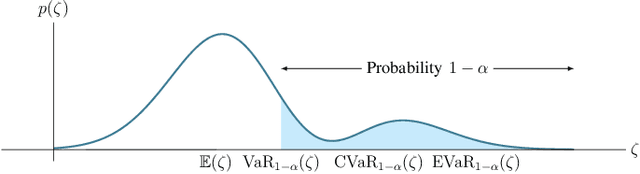
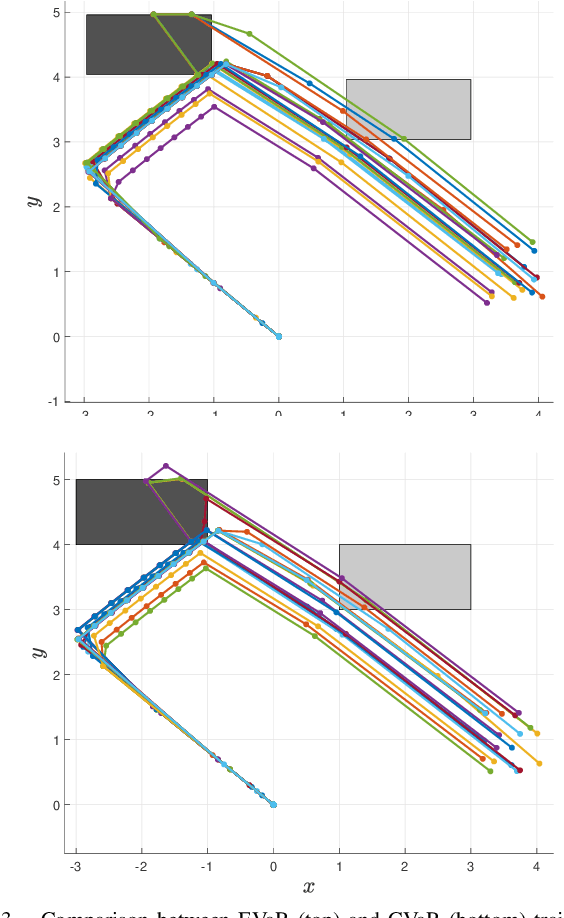
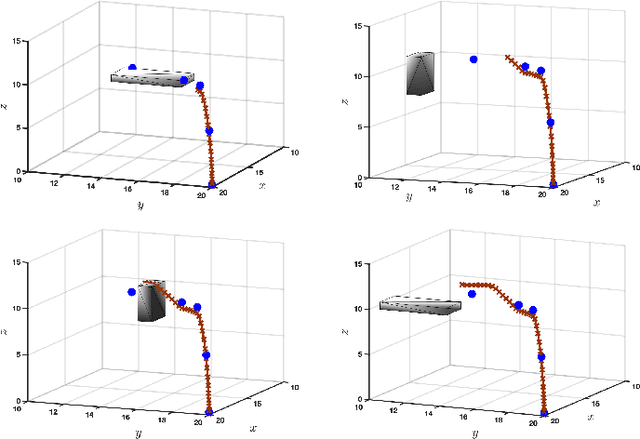
We consider the problem of risk-sensitive motion planning in the presence of randomly moving obstacles. To this end, we adopt a model predictive control (MPC) scheme and pose the obstacle avoidance constraint in the MPC problem as a distributionally robust constraint with a KL divergence ambiguity set. This constraint is the dual representation of the Entropic Value-at-Risk (EVaR). Building upon this viewpoint, we propose an algorithm to follow waypoints and discuss its feasibility and completion in finite time. We compare the policies obtained using EVaR with those obtained using another common coherent risk measure, Conditional Value-at-Risk (CVaR), via numerical experiments for a 2D system. We also implement the waypoint following algorithm on a 3D quadcopter simulation.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge