Conformal Classification with Equalized Coverage for Adaptively Selected Groups

This paper introduces a conformal inference method to evaluate uncertainty in classification by generating prediction sets with valid coverage conditional on adaptively chosen features. These features are carefully selected to reflect potential model limitations or biases. This can be useful to find a practical compromise between efficiency -- by providing informative predictions -- and algorithmic fairness -- by ensuring equalized coverage for the most sensitive groups. We demonstrate the validity and effectiveness of this method on simulated and real data sets.

Conformalized Adaptive Forecasting of Heterogeneous Trajectories

This paper presents a new conformal method for generating simultaneous forecasting bands guaranteed to cover the entire path of a new random trajectory with sufficiently high probability. Prompted by the need for dependable uncertainty estimates in motion planning applications where the behavior of diverse objects may be more or less unpredictable, we blend different techniques from online conformal prediction of single and multiple time series, as well as ideas for addressing heteroscedasticity in regression. This solution is both principled, providing precise finite-sample guarantees, and effective, often leading to more informative predictions than prior methods.

Conformal inference is (almost) free for neural networks trained with early stopping

Early stopping based on hold-out data is a popular regularization technique designed to mitigate overfitting and increase the predictive accuracy of neural networks. Models trained with early stopping often provide relatively accurate predictions, but they generally still lack precise statistical guarantees unless they are further calibrated using independent hold-out data. This paper addresses the above limitation with conformalized early stopping: a novel method that combines early stopping with conformal calibration while efficiently recycling the same hold-out data. This leads to models that are both accurate and able to provide exact predictive inferences without multiple data splits nor overly conservative adjustments. Practical implementations are developed for different learning tasks -- outlier detection, multi-class classification, regression -- and their competitive performance is demonstrated on real data.

Training Uncertainty-Aware Classifiers with Conformalized Deep Learning

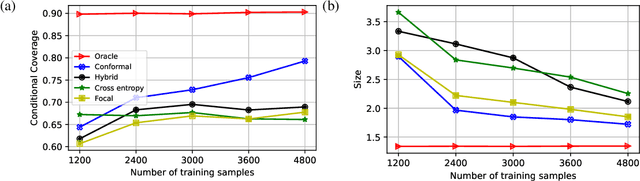
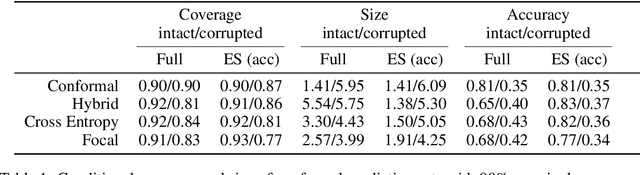
Deep neural networks are powerful tools to detect hidden patterns in data and leverage them to make predictions, but they are not designed to understand uncertainty and estimate reliable probabilities. In particular, they tend to be overconfident. We address this problem by developing a novel training algorithm that can lead to more dependable uncertainty estimates, without sacrificing predictive power. The idea is to mitigate overconfidence by minimizing a loss function, inspired by advances in conformal inference, that quantifies model uncertainty by carefully leveraging hold-out data. Experiments with synthetic and real data demonstrate this method leads to smaller conformal prediction sets with higher conditional coverage, after exact calibration with hold-out data, compared to state-of-the-art alternatives.