Sample Efficient Subspace-based Representations for Nonlinear Meta-Learning
Paper and Code
Feb 26, 2021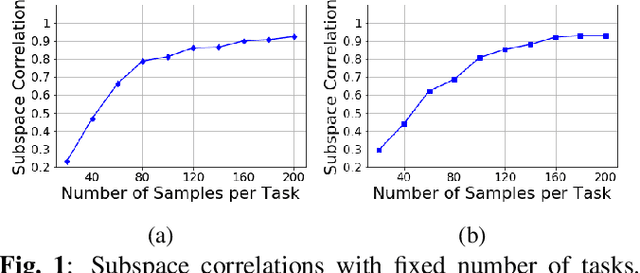
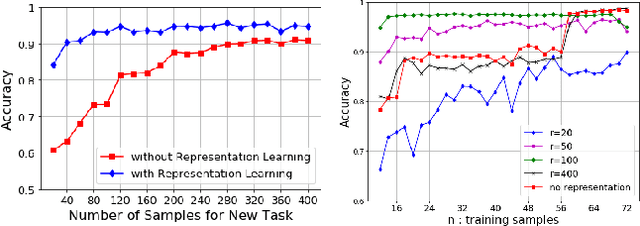
Constructing good representations is critical for learning complex tasks in a sample efficient manner. In the context of meta-learning, representations can be constructed from common patterns of previously seen tasks so that a future task can be learned quickly. While recent works show the benefit of subspace-based representations, such results are limited to linear-regression tasks. This work explores a more general class of nonlinear tasks with applications ranging from binary classification, generalized linear models and neural nets. We prove that subspace-based representations can be learned in a sample-efficient manner and provably benefit future tasks in terms of sample complexity. Numerical results verify the theoretical predictions in classification and neural-network regression tasks.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge