Feiqing Huang
Contrastive Learning on Multimodal Analysis of Electronic Health Records
Mar 22, 2024



Abstract:Electronic health record (EHR) systems contain a wealth of multimodal clinical data including structured data like clinical codes and unstructured data such as clinical notes. However, many existing EHR-focused studies has traditionally either concentrated on an individual modality or merged different modalities in a rather rudimentary fashion. This approach often results in the perception of structured and unstructured data as separate entities, neglecting the inherent synergy between them. Specifically, the two important modalities contain clinically relevant, inextricably linked and complementary health information. A more complete picture of a patient's medical history is captured by the joint analysis of the two modalities of data. Despite the great success of multimodal contrastive learning on vision-language, its potential remains under-explored in the realm of multimodal EHR, particularly in terms of its theoretical understanding. To accommodate the statistical analysis of multimodal EHR data, in this paper, we propose a novel multimodal feature embedding generative model and design a multimodal contrastive loss to obtain the multimodal EHR feature representation. Our theoretical analysis demonstrates the effectiveness of multimodal learning compared to single-modality learning and connects the solution of the loss function to the singular value decomposition of a pointwise mutual information matrix. This connection paves the way for a privacy-preserving algorithm tailored for multimodal EHR feature representation learning. Simulation studies show that the proposed algorithm performs well under a variety of configurations. We further validate the clinical utility of the proposed algorithm in real-world EHR data.
A New Measure of Model Redundancy for Compressed Convolutional Neural Networks
Dec 09, 2021
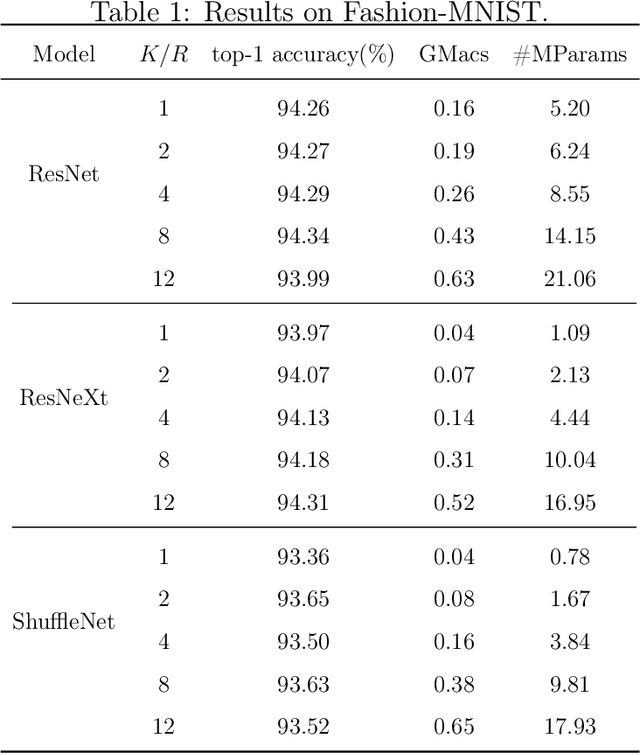
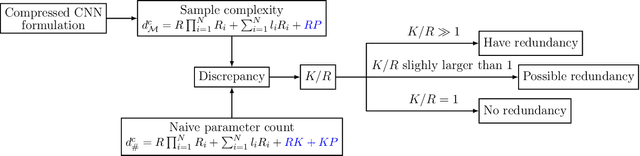
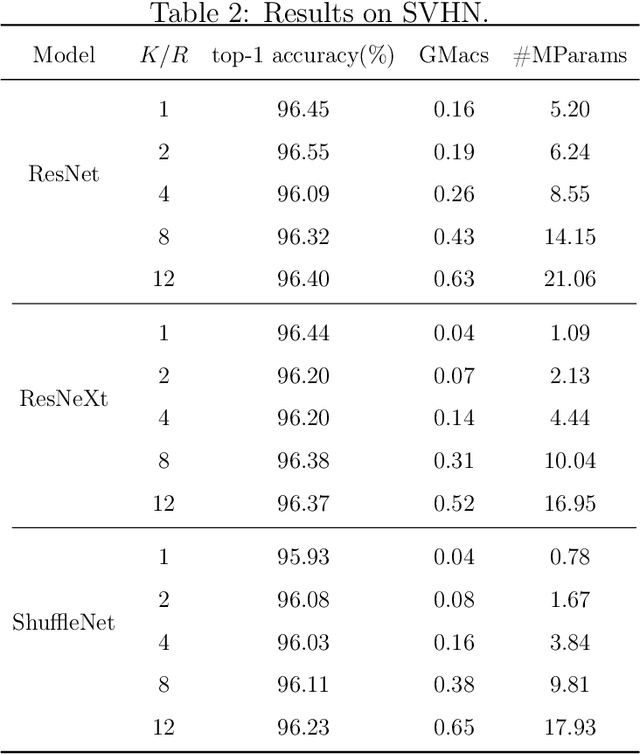
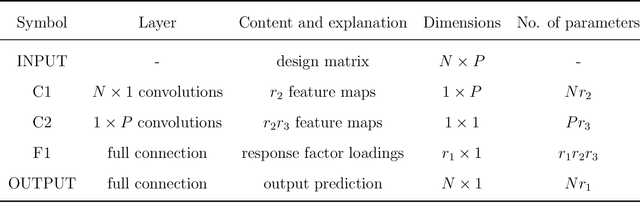
Abstract:While recently many designs have been proposed to improve the model efficiency of convolutional neural networks (CNNs) on a fixed resource budget, theoretical understanding of these designs is still conspicuously lacking. This paper aims to provide a new framework for answering the question: Is there still any remaining model redundancy in a compressed CNN? We begin by developing a general statistical formulation of CNNs and compressed CNNs via the tensor decomposition, such that the weights across layers can be summarized into a single tensor. Then, through a rigorous sample complexity analysis, we reveal an important discrepancy between the derived sample complexity and the naive parameter counting, which serves as a direct indicator of the model redundancy. Motivated by this finding, we introduce a new model redundancy measure for compressed CNNs, called the $K/R$ ratio, which further allows for nonlinear activations. The usefulness of this new measure is supported by ablation studies on popular block designs and datasets.
Do RNN and LSTM have Long Memory?
Jun 10, 2020
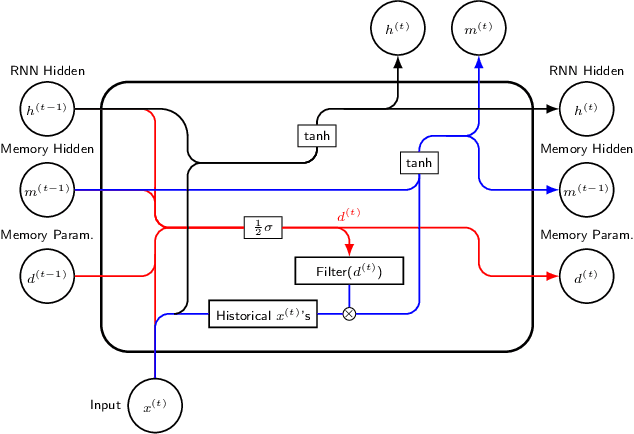
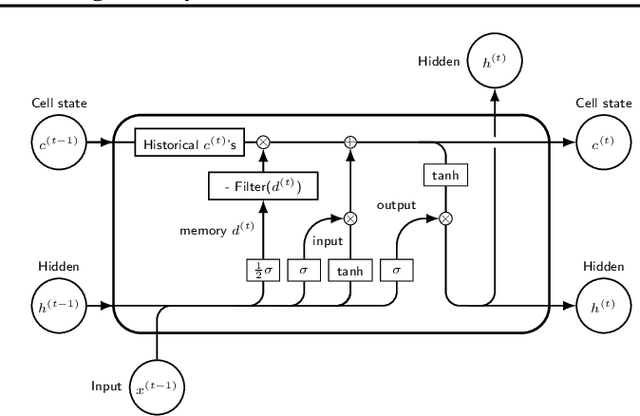
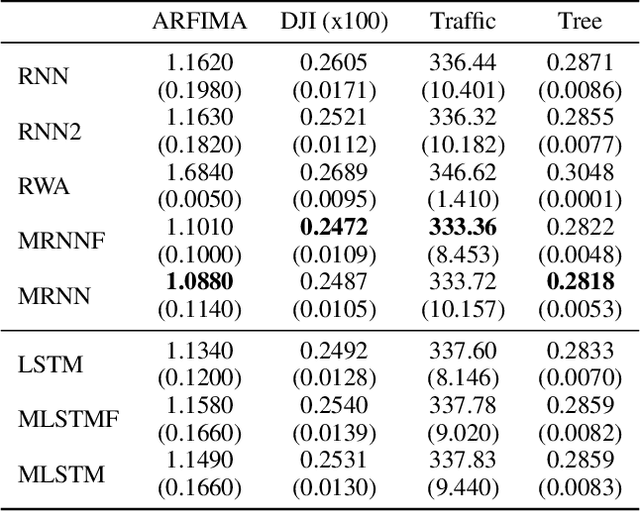
Abstract:The LSTM network was proposed to overcome the difficulty in learning long-term dependence, and has made significant advancements in applications. With its success and drawbacks in mind, this paper raises the question - do RNN and LSTM have long memory? We answer it partially by proving that RNN and LSTM do not have long memory from a statistical perspective. A new definition for long memory networks is further introduced, and it requires the model weights to decay at a polynomial rate. To verify our theory, we convert RNN and LSTM into long memory networks by making a minimal modification, and their superiority is illustrated in modeling long-term dependence of various datasets.
Compact Autoregressive Network
Sep 06, 2019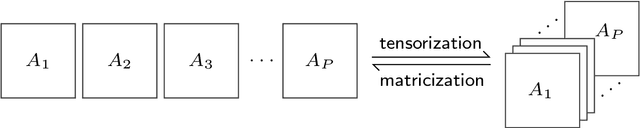
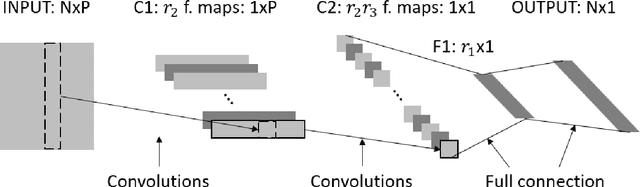
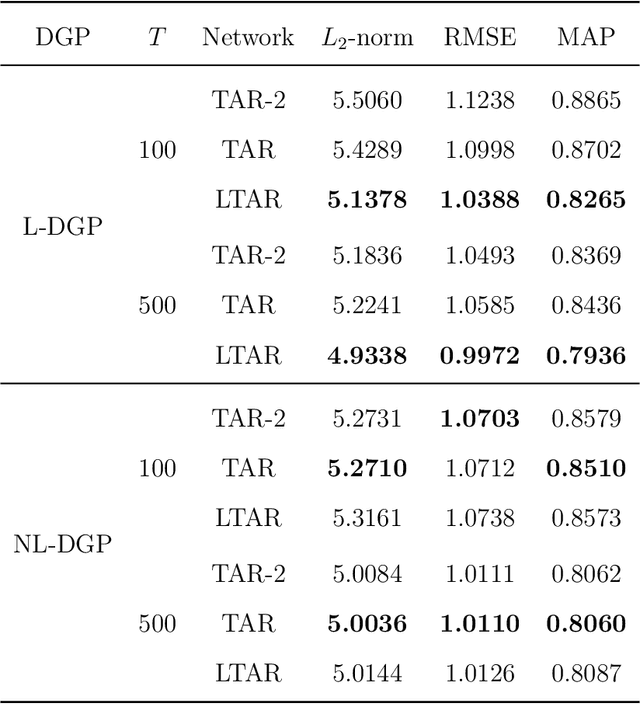
Abstract:Autoregressive networks can achieve promising performance in many sequence modeling tasks with short-range dependence. However, when handling high-dimensional inputs and outputs, the huge amount of parameters in the network lead to expensive computational cost and low learning efficiency. The problem can be alleviated slightly by introducing one more narrow hidden layer to the network, but the sample size required to achieve a certain training error is still large. To address this challenge, we rearrange the weight matrices of a linear autoregressive network into a tensor form, and then make use of Tucker decomposition to represent low-rank structures. This leads to a novel compact autoregressive network, called Tucker AutoRegressive (TAR) net. Interestingly, the TAR net can be applied to sequences with long-range dependence since the dimension along the sequential order is reduced. Theoretical studies show that the TAR net improves the learning efficiency, and requires much fewer samples for model training. Experiments on synthetic and real-world datasets demonstrate the promising performance of the proposed compact network.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge