Compact Autoregressive Network
Paper and Code
Sep 06, 2019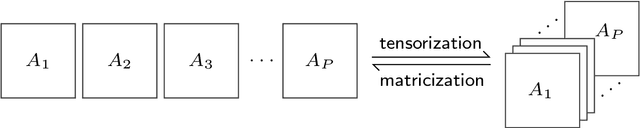
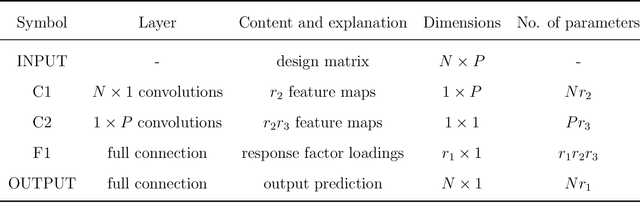
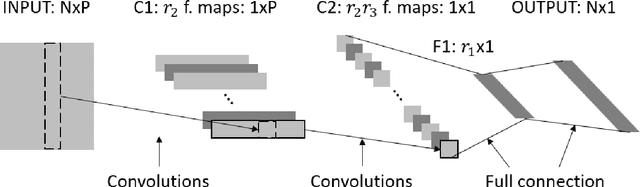
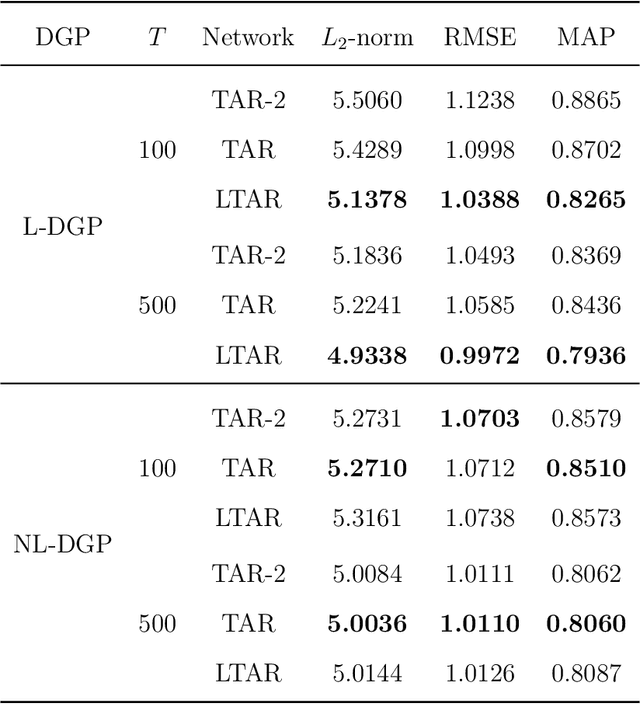
Autoregressive networks can achieve promising performance in many sequence modeling tasks with short-range dependence. However, when handling high-dimensional inputs and outputs, the huge amount of parameters in the network lead to expensive computational cost and low learning efficiency. The problem can be alleviated slightly by introducing one more narrow hidden layer to the network, but the sample size required to achieve a certain training error is still large. To address this challenge, we rearrange the weight matrices of a linear autoregressive network into a tensor form, and then make use of Tucker decomposition to represent low-rank structures. This leads to a novel compact autoregressive network, called Tucker AutoRegressive (TAR) net. Interestingly, the TAR net can be applied to sequences with long-range dependence since the dimension along the sequential order is reduced. Theoretical studies show that the TAR net improves the learning efficiency, and requires much fewer samples for model training. Experiments on synthetic and real-world datasets demonstrate the promising performance of the proposed compact network.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge