Guangjian Tian
SpatialCoT: Advancing Spatial Reasoning through Coordinate Alignment and Chain-of-Thought for Embodied Task Planning
Jan 17, 2025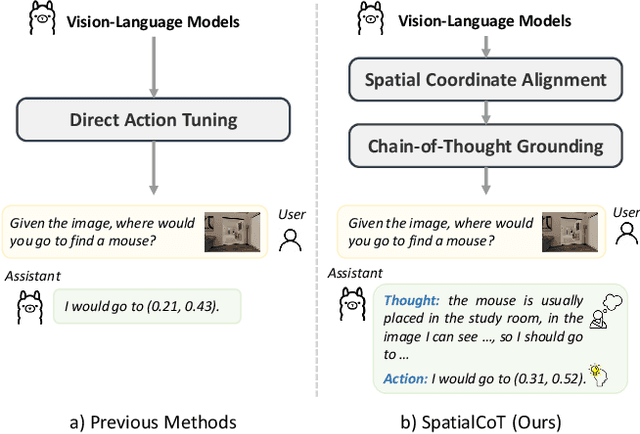
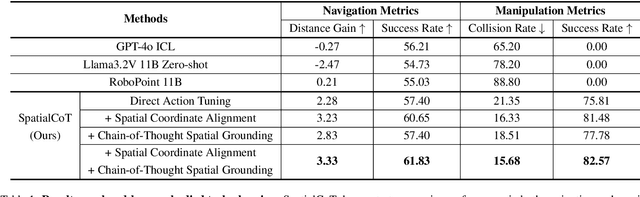
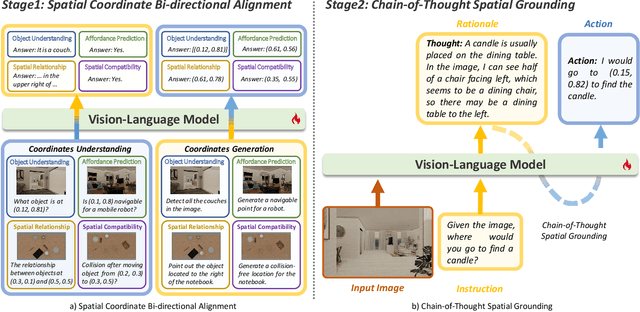
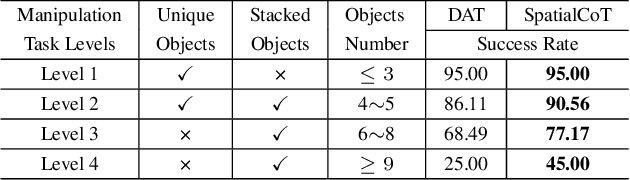
Abstract:Spatial reasoning is an essential problem in embodied AI research. Efforts to enhance spatial reasoning abilities through supplementary spatial data and fine-tuning have proven limited and ineffective when addressing complex embodied tasks, largely due to their dependence on language-based outputs. While some approaches have introduced a point-based action space to mitigate this issue, they fall short in managing more intricate tasks within complex environments. This deficiency arises from their failure to fully exploit the inherent thinking and reasoning capabilities that are fundamental strengths of Vision-Language Models (VLMs). To address these limitations, we propose a novel approach named SpatialCoT, specifically designed to bolster the spatial reasoning capabilities of VLMs. Our approach comprises two stages: spatial coordinate bi-directional alignment, which aligns vision-language inputs with spatial coordinates, and chain-of-thought spatial grounding, which harnesses the reasoning capabilities of language models for advanced spatial reasoning. We evaluate SpatialCoT on challenging navigation and manipulation tasks, both in simulation and real-world settings. Experimental results demonstrate that our method significantly outperforms previous state-of-the-art approaches in both tasks.
ROS-LLM: A ROS framework for embodied AI with task feedback and structured reasoning
Jun 28, 2024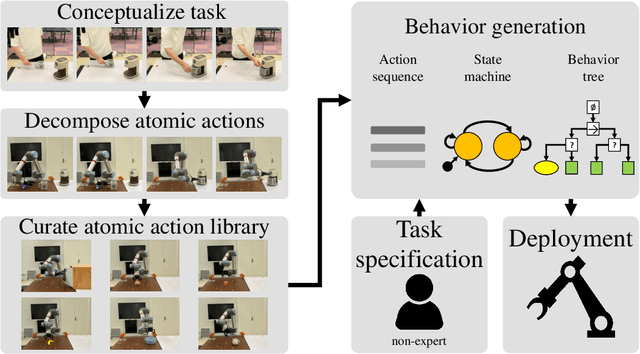
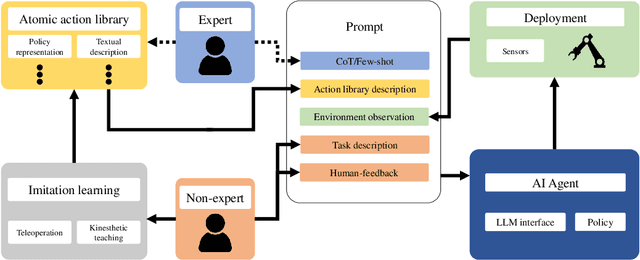
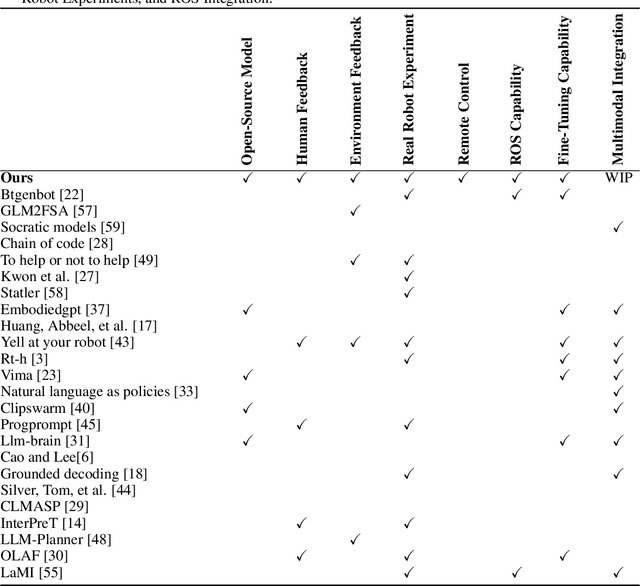
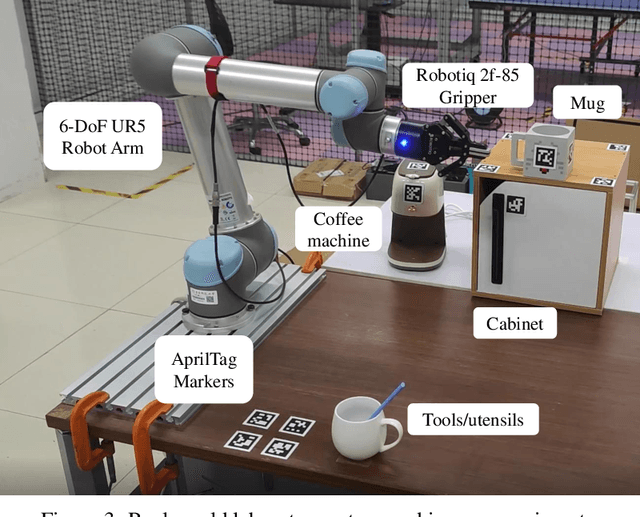
Abstract:We present a framework for intuitive robot programming by non-experts, leveraging natural language prompts and contextual information from the Robot Operating System (ROS). Our system integrates large language models (LLMs), enabling non-experts to articulate task requirements to the system through a chat interface. Key features of the framework include: integration of ROS with an AI agent connected to a plethora of open-source and commercial LLMs, automatic extraction of a behavior from the LLM output and execution of ROS actions/services, support for three behavior modes (sequence, behavior tree, state machine), imitation learning for adding new robot actions to the library of possible actions, and LLM reflection via human and environment feedback. Extensive experiments validate the framework, showcasing robustness, scalability, and versatility in diverse scenarios, including long-horizon tasks, tabletop rearrangements, and remote supervisory control. To facilitate the adoption of our framework and support the reproduction of our results, we have made our code open-source. You can access it at: https://github.com/huawei-noah/HEBO/tree/master/ROSLLM.
Cross-Layer Retrospective Retrieving via Layer Attention
Feb 28, 2023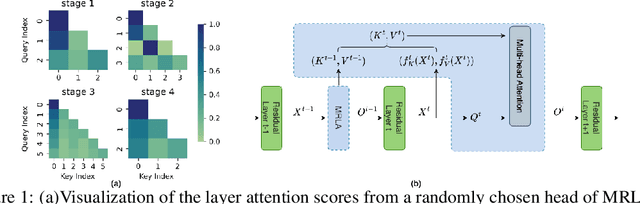
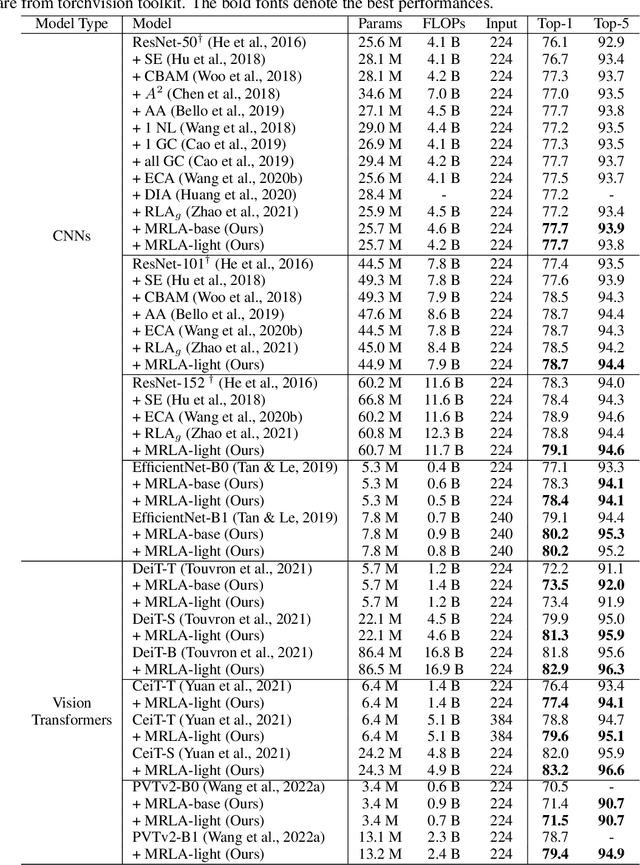
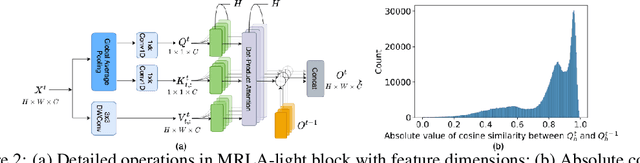
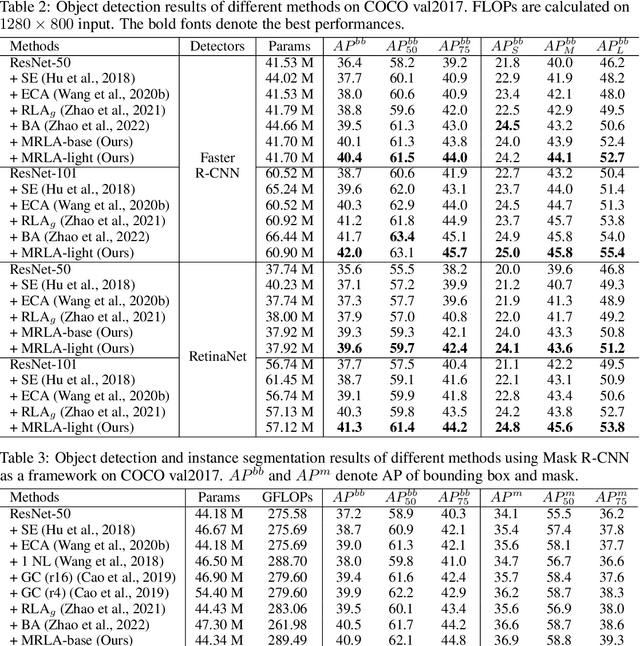
Abstract:More and more evidence has shown that strengthening layer interactions can enhance the representation power of a deep neural network, while self-attention excels at learning interdependencies by retrieving query-activated information. Motivated by this, we devise a cross-layer attention mechanism, called multi-head recurrent layer attention (MRLA), that sends a query representation of the current layer to all previous layers to retrieve query-related information from different levels of receptive fields. A light-weighted version of MRLA is also proposed to reduce the quadratic computation cost. The proposed layer attention mechanism can enrich the representation power of many state-of-the-art vision networks, including CNNs and vision transformers. Its effectiveness has been extensively evaluated in image classification, object detection and instance segmentation tasks, where improvements can be consistently observed. For example, our MRLA can improve 1.6% Top-1 accuracy on ResNet-50, while only introducing 0.16M parameters and 0.07B FLOPs. Surprisingly, it can boost the performances by a large margin of 3-4% box AP and mask AP in dense prediction tasks. Our code is available at https://github.com/joyfang1106/MRLA.
Fast Gumbel-Max Sketch and its Applications
Feb 10, 2023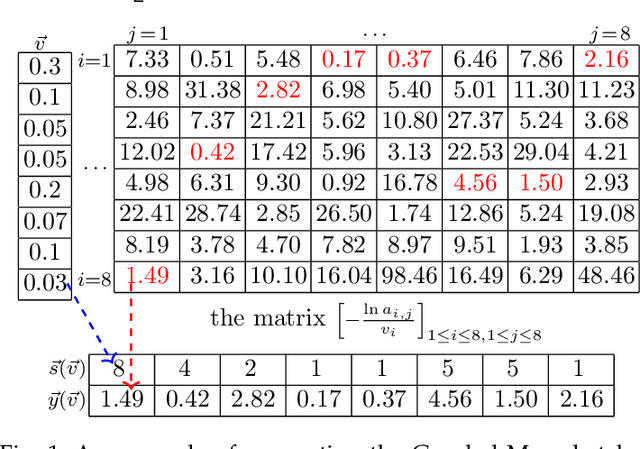
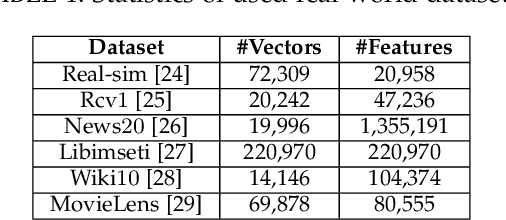
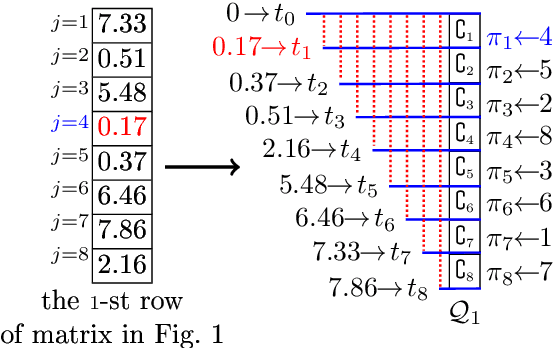
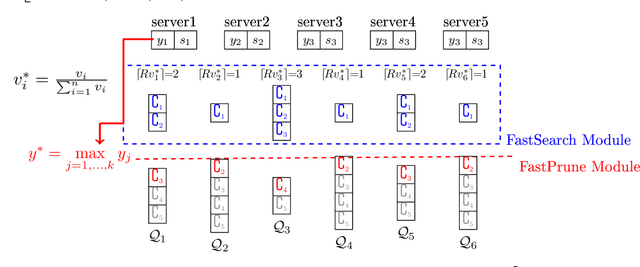
Abstract:The well-known Gumbel-Max Trick for sampling elements from a categorical distribution (or more generally a non-negative vector) and its variants have been widely used in areas such as machine learning and information retrieval. To sample a random element $i$ in proportion to its positive weight $v_i$, the Gumbel-Max Trick first computes a Gumbel random variable $g_i$ for each positive weight element $i$, and then samples the element $i$ with the largest value of $g_i+\ln v_i$. Recently, applications including similarity estimation and weighted cardinality estimation require to generate $k$ independent Gumbel-Max variables from high dimensional vectors. However, it is computationally expensive for a large $k$ (e.g., hundreds or even thousands) when using the traditional Gumbel-Max Trick. To solve this problem, we propose a novel algorithm, FastGM, which reduces the time complexity from $O(kn^+)$ to $O(k \ln k + n^+)$, where $n^+$ is the number of positive elements in the vector of interest. FastGM stops the procedure of Gumbel random variables computing for many elements, especially for those with small weights. We perform experiments on a variety of real-world datasets and the experimental results demonstrate that FastGM is orders of magnitude faster than state-of-the-art methods without sacrificing accuracy or incurring additional expenses.
Synergetic Learning of Heterogeneous Temporal Sequences for Multi-Horizon Probabilistic Forecasting
Jan 31, 2021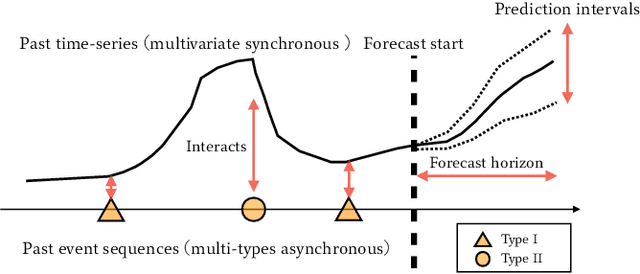
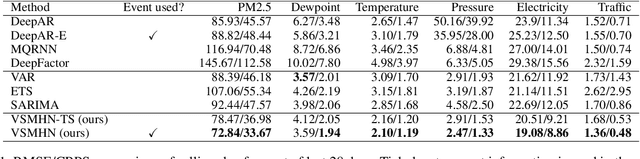
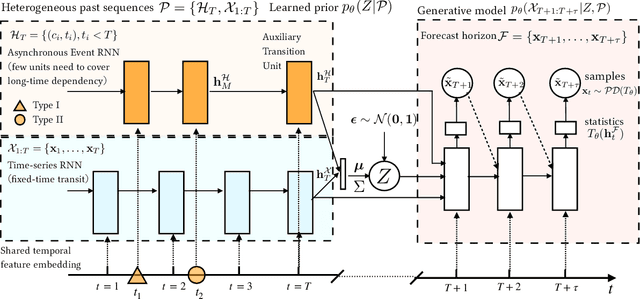
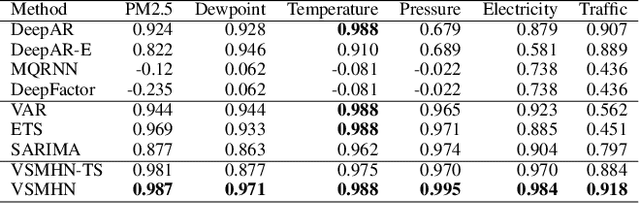
Abstract:Time-series is ubiquitous across applications, such as transportation, finance and healthcare. Time-series is often influenced by external factors, especially in the form of asynchronous events, making forecasting difficult. However, existing models are mainly designated for either synchronous time-series or asynchronous event sequence, and can hardly provide a synthetic way to capture the relation between them. We propose Variational Synergetic Multi-Horizon Network (VSMHN), a novel deep conditional generative model. To learn complex correlations across heterogeneous sequences, a tailored encoder is devised to combine the advances in deep point processes models and variational recurrent neural networks. In addition, an aligned time coding and an auxiliary transition scheme are carefully devised for batched training on unaligned sequences. Our model can be trained effectively using stochastic variational inference and generates probabilistic predictions with Monte-Carlo simulation. Furthermore, our model produces accurate, sharp and more realistic probabilistic forecasts. We also show that modeling asynchronous event sequences is crucial for multi-horizon time-series forecasting.
Do RNN and LSTM have Long Memory?
Jun 10, 2020
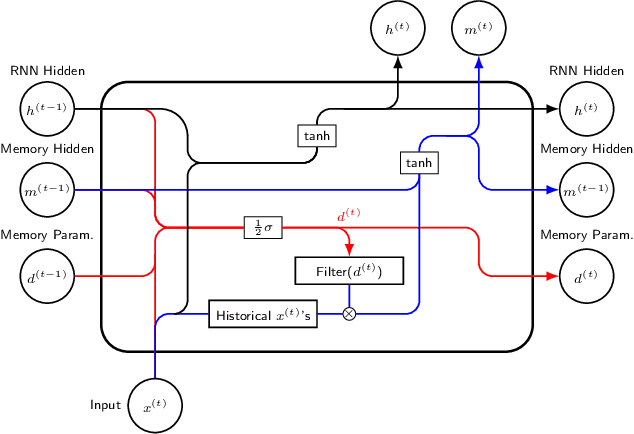
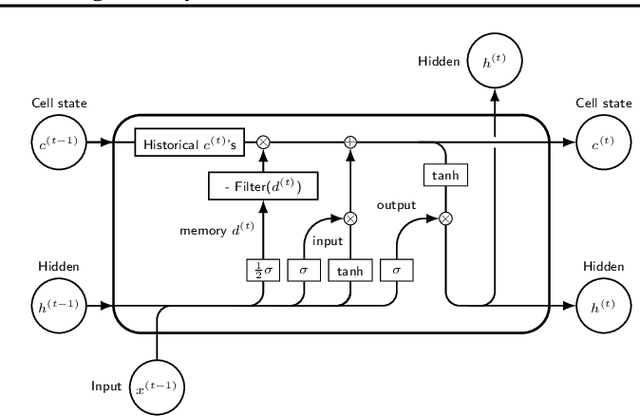
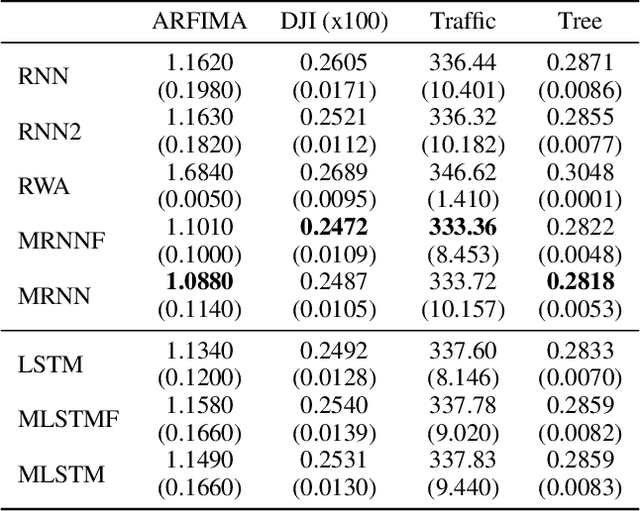
Abstract:The LSTM network was proposed to overcome the difficulty in learning long-term dependence, and has made significant advancements in applications. With its success and drawbacks in mind, this paper raises the question - do RNN and LSTM have long memory? We answer it partially by proving that RNN and LSTM do not have long memory from a statistical perspective. A new definition for long memory networks is further introduced, and it requires the model weights to decay at a polynomial rate. To verify our theory, we convert RNN and LSTM into long memory networks by making a minimal modification, and their superiority is illustrated in modeling long-term dependence of various datasets.
Fast Generating A Large Number of Gumbel-Max Variables
Feb 02, 2020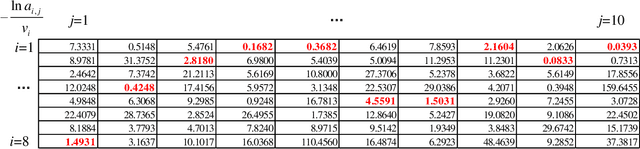
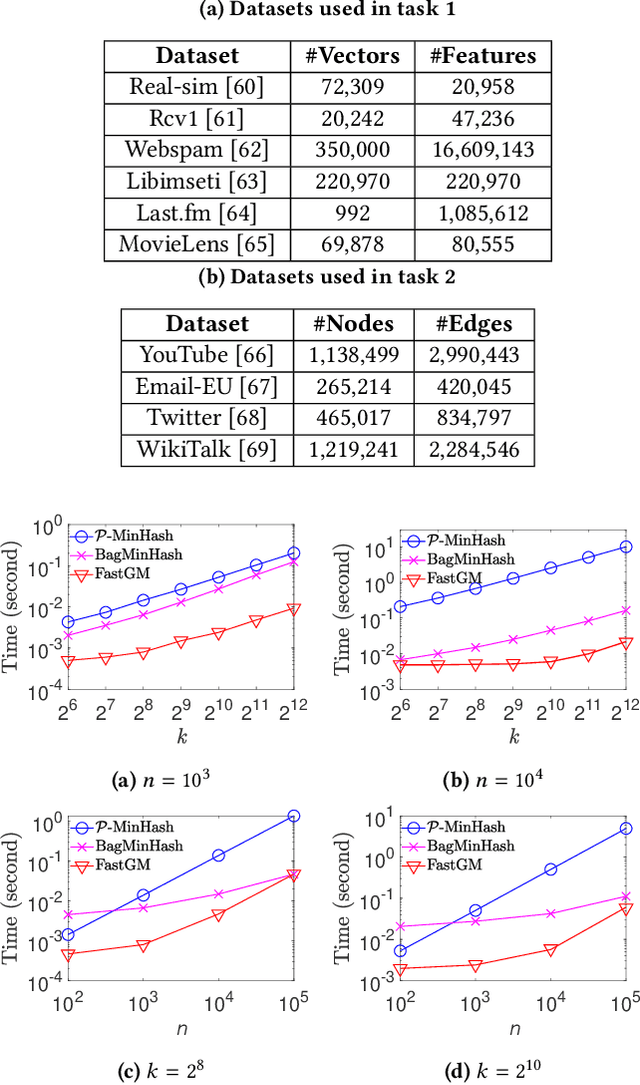
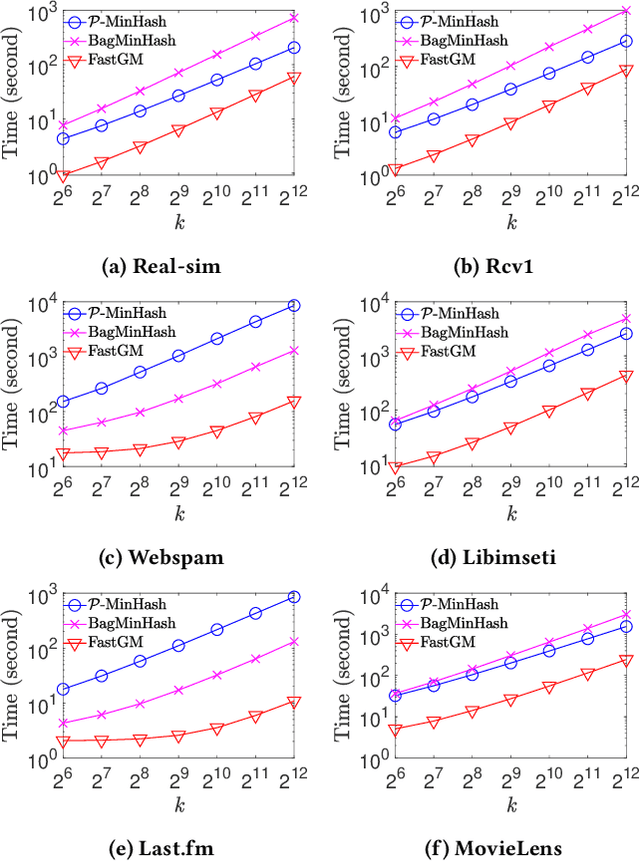
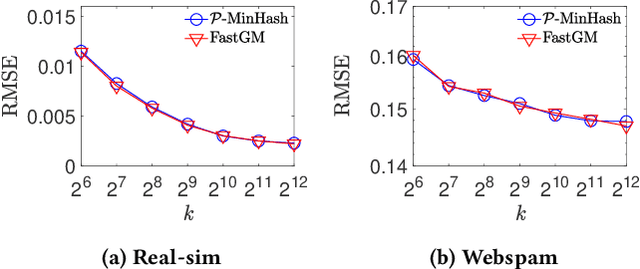
Abstract:The well-known Gumbel-Max Trick for sampling elements from a categorical distribution (or more generally a nonnegative vector) and its variants have been widely used in areas such as machine learning and information retrieval. To sample a random element $i$ (or a Gumbel-Max variable $i$) in proportion to its positive weight $v_i$, the Gumbel-Max Trick first computes a Gumbel random variable $g_i$ for each positive weight element $i$, and then samples the element $i$ with the largest value of $g_i+\ln v_i$. Recently, applications including similarity estimation and graph embedding require to generate $k$ independent Gumbel-Max variables from high dimensional vectors. However, it is computationally expensive for a large $k$ (e.g., hundreds or even thousands) when using the traditional Gumbel-Max Trick. To solve this problem, we propose a novel algorithm, \emph{FastGM}, that reduces the time complexity from $O(kn^+)$ to $O(k \ln k + n^+)$, where $n^+$ is the number of positive elements in the vector of interest. Instead of computing $k$ independent Gumbel random variables directly, we find that there exists a technique to generate these variables in descending order. Using this technique, our method FastGM computes variables $g_i+\ln v_i$ for all positive elements $i$ in descending order. As a result, FastGM significantly reduces the computation time because we can stop the procedure of Gumbel random variables computing for many elements especially for those with small weights. Experiments on a variety of real-world datasets show that FastGM is orders of magnitude faster than state-of-the-art methods without sacrificing accuracy and incurring additional expenses.
Compact Autoregressive Network
Sep 06, 2019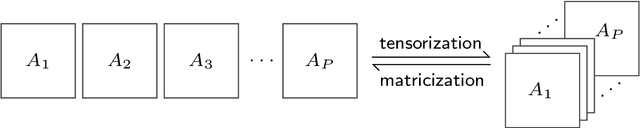
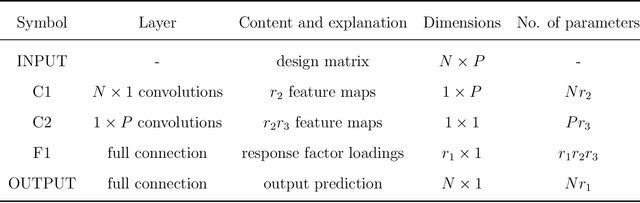
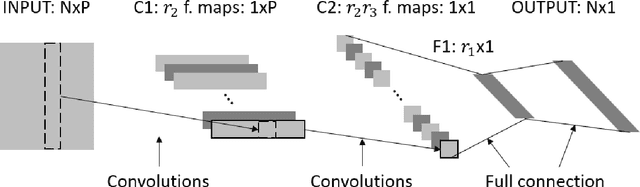
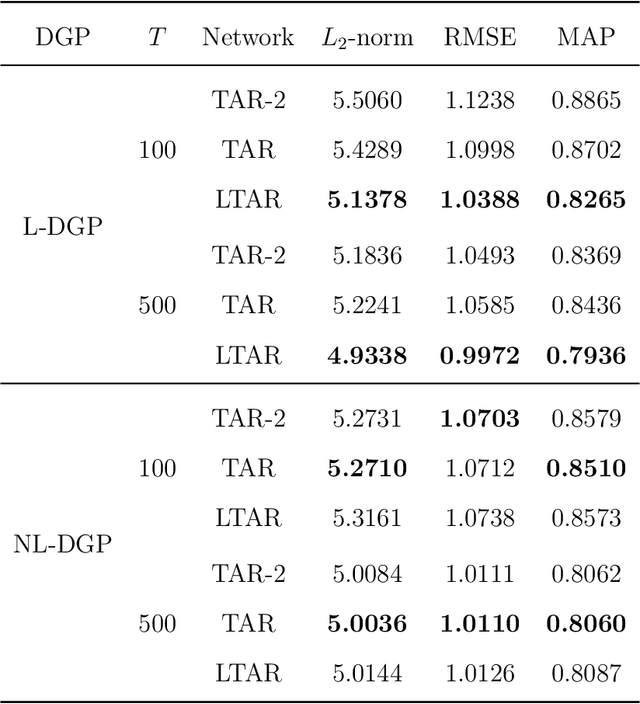
Abstract:Autoregressive networks can achieve promising performance in many sequence modeling tasks with short-range dependence. However, when handling high-dimensional inputs and outputs, the huge amount of parameters in the network lead to expensive computational cost and low learning efficiency. The problem can be alleviated slightly by introducing one more narrow hidden layer to the network, but the sample size required to achieve a certain training error is still large. To address this challenge, we rearrange the weight matrices of a linear autoregressive network into a tensor form, and then make use of Tucker decomposition to represent low-rank structures. This leads to a novel compact autoregressive network, called Tucker AutoRegressive (TAR) net. Interestingly, the TAR net can be applied to sequences with long-range dependence since the dimension along the sequential order is reduced. Theoretical studies show that the TAR net improves the learning efficiency, and requires much fewer samples for model training. Experiments on synthetic and real-world datasets demonstrate the promising performance of the proposed compact network.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge