Fast Gumbel-Max Sketch and its Applications
Paper and Code
Feb 10, 2023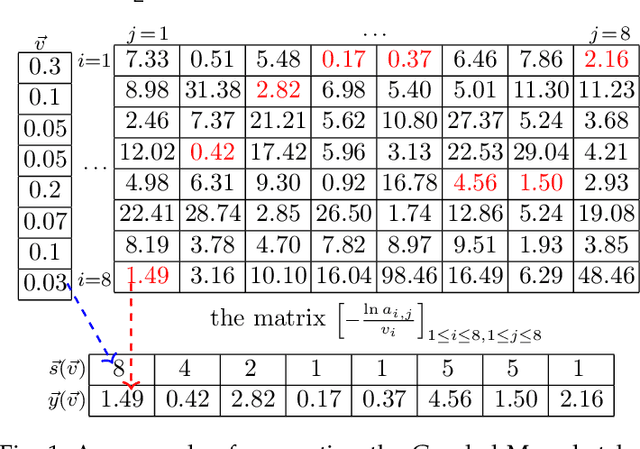
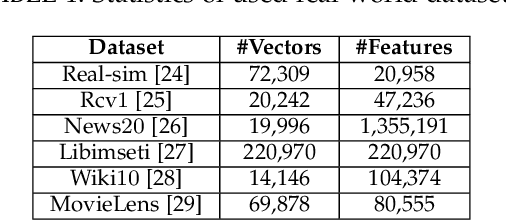
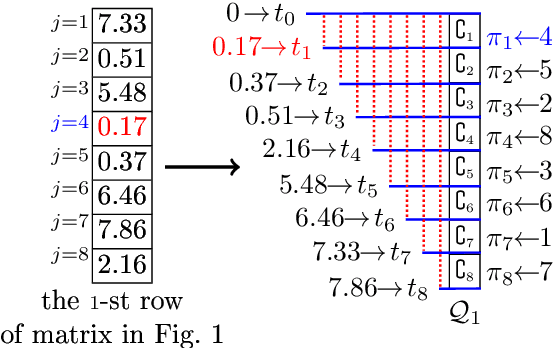
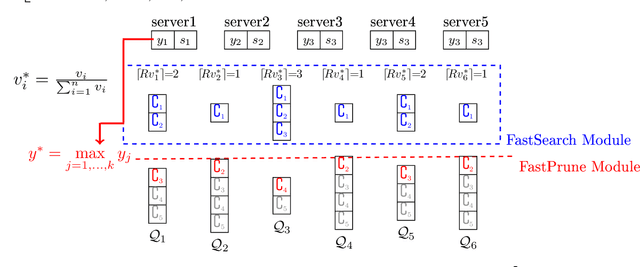
The well-known Gumbel-Max Trick for sampling elements from a categorical distribution (or more generally a non-negative vector) and its variants have been widely used in areas such as machine learning and information retrieval. To sample a random element $i$ in proportion to its positive weight $v_i$, the Gumbel-Max Trick first computes a Gumbel random variable $g_i$ for each positive weight element $i$, and then samples the element $i$ with the largest value of $g_i+\ln v_i$. Recently, applications including similarity estimation and weighted cardinality estimation require to generate $k$ independent Gumbel-Max variables from high dimensional vectors. However, it is computationally expensive for a large $k$ (e.g., hundreds or even thousands) when using the traditional Gumbel-Max Trick. To solve this problem, we propose a novel algorithm, FastGM, which reduces the time complexity from $O(kn^+)$ to $O(k \ln k + n^+)$, where $n^+$ is the number of positive elements in the vector of interest. FastGM stops the procedure of Gumbel random variables computing for many elements, especially for those with small weights. We perform experiments on a variety of real-world datasets and the experimental results demonstrate that FastGM is orders of magnitude faster than state-of-the-art methods without sacrificing accuracy or incurring additional expenses.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge