Yao Zheng
A Survey on Reconfigurable Intelligent Surfaces in Practical Systems: Security and Privacy Perspectives
Dec 12, 2025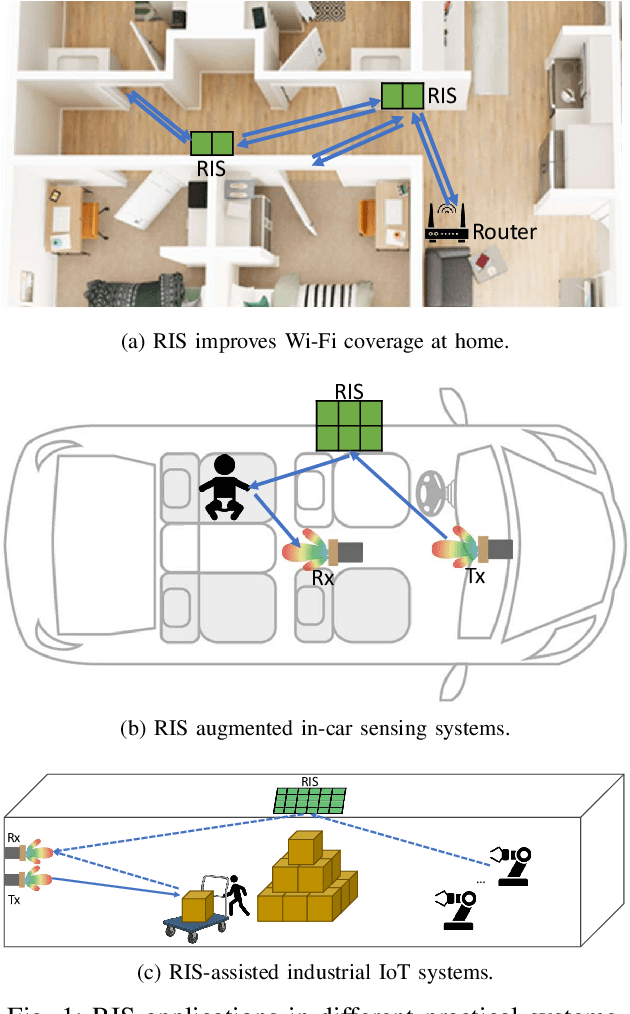
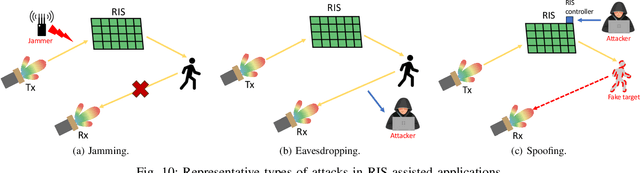
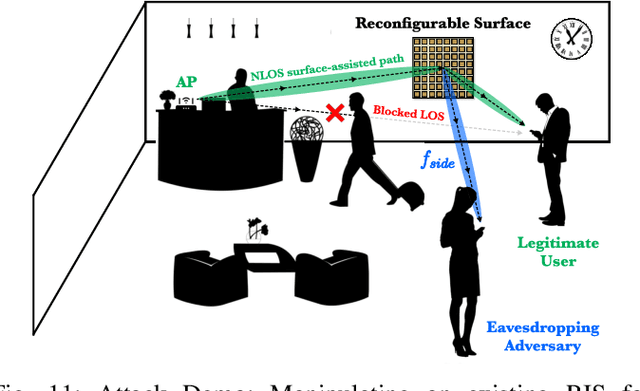
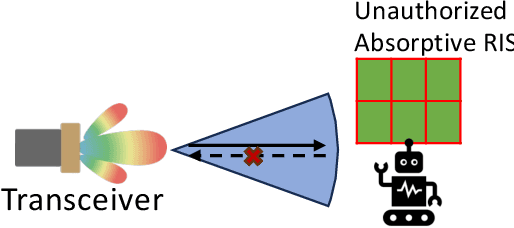
Abstract:Reconfigurable Intelligent Surfaces (RIS) have emerged as a transformative technology capable of reshaping wireless environments through dynamic manipulation of electromagnetic waves. While extensive research has explored their theoretical benefits for communication and sensing, practical deployments in smart environments such as homes, vehicles, and industrial settings remain limited and under-examined, particularly from security and privacy perspectives. This survey provides a comprehensive examination of RIS applications in real-world systems, with a focus on the security and privacy threats, vulnerabilities, and defensive strategies relevant to practical use. We analyze scenarios with two types of systems (with and without legitimate RIS) and two types of attackers (with and without malicious RIS), and demonstrate how RIS may introduce new attacks to practical systems, including eavesdropping, jamming, and spoofing attacks. In response, we review defenses against RIS-related attacks in these systems, such as applying additional security algorithms, disrupting attackers, and early detection of unauthorized RIS. We also discuss scenarios in which the legitimate user applies an additional RIS to defend against attacks. To support future research, we also provide a collection of open-source tools, datasets, demos, and papers at: https://awesome-ris-security.github.io/. By highlighting RIS's functionality and its security/privacy challenges and opportunities, this survey aims to guide researchers and engineers toward the development of secure, resilient, and privacy-preserving RIS-enabled practical wireless systems and environments.
Online Conformal Model Selection for Nonstationary Time Series
Jun 05, 2025Abstract:This paper introduces the MPS (Model Prediction Set), a novel framework for online model selection for nonstationary time series. Classical model selection methods, such as information criteria and cross-validation, rely heavily on the stationarity assumption and often fail in dynamic environments which undergo gradual or abrupt changes over time. Yet real-world data are rarely stationary, and model selection under nonstationarity remains a largely open problem. To tackle this challenge, we combine conformal inference with model confidence sets to develop a procedure that adaptively selects models best suited to the evolving dynamics at any given time. Concretely, the MPS updates in real time a confidence set of candidate models that covers the best model for the next time period with a specified long-run probability, while adapting to nonstationarity of unknown forms. Through simulations and real-world data analysis, we demonstrate that MPS reliably and efficiently identifies optimal models under nonstationarity, an essential capability lacking in offline methods. Moreover, MPS frequently produces high-quality sets with small cardinality, whose evolution offers deeper insights into changing dynamics. As a generic framework, MPS accommodates any data-generating process, data structure, model class, training method, and evaluation metric, making it broadly applicable across diverse problem settings.
GaussianAD: Gaussian-Centric End-to-End Autonomous Driving
Dec 13, 2024



Abstract:Vision-based autonomous driving shows great potential due to its satisfactory performance and low costs. Most existing methods adopt dense representations (e.g., bird's eye view) or sparse representations (e.g., instance boxes) for decision-making, which suffer from the trade-off between comprehensiveness and efficiency. This paper explores a Gaussian-centric end-to-end autonomous driving (GaussianAD) framework and exploits 3D semantic Gaussians to extensively yet sparsely describe the scene. We initialize the scene with uniform 3D Gaussians and use surrounding-view images to progressively refine them to obtain the 3D Gaussian scene representation. We then use sparse convolutions to efficiently perform 3D perception (e.g., 3D detection, semantic map construction). We predict 3D flows for the Gaussians with dynamic semantics and plan the ego trajectory accordingly with an objective of future scene forecasting. Our GaussianAD can be trained in an end-to-end manner with optional perception labels when available. Extensive experiments on the widely used nuScenes dataset verify the effectiveness of our end-to-end GaussianAD on various tasks including motion planning, 3D occupancy prediction, and 4D occupancy forecasting. Code: https://github.com/wzzheng/GaussianAD.
Trajectory optimization of tail-sitter considering speed constraints
Jun 12, 2024



Abstract:Tail-sitters combine the advantages of fixed-wing unmanned aerial vehicles (UAVs) and vertical take-off and landing UAVs, and have been widely designed and researched in recent years. With the change in modern UAV application scenarios, it is required that UAVs have fast maneuverable three-dimensional flight capabilities. Due to the highly nonlinear aerodynamics produced by the fuselage and wings of the tail-sitter, how to quickly generate a smooth and executable trajectory is a problem that needs to be solved urgently. We constrain the speed of the tail-sitter, eliminate the differential dynamics constraints in the trajectory generation process of the tail-sitter through differential flatness, and allocate the time variable of the trajectory through the state-of-the-art trajectory generation method named MINCO. Because we discretize the trajectory in time, we convert the speed constraint on the vehicle into a soft constraint, thereby achieving the time-optimal trajectory for the tail-sitter to fly through any given waypoints.
An Interpretable and Efficient Infinite-Order Vector Autoregressive Model for High-Dimensional Time Series
Sep 16, 2022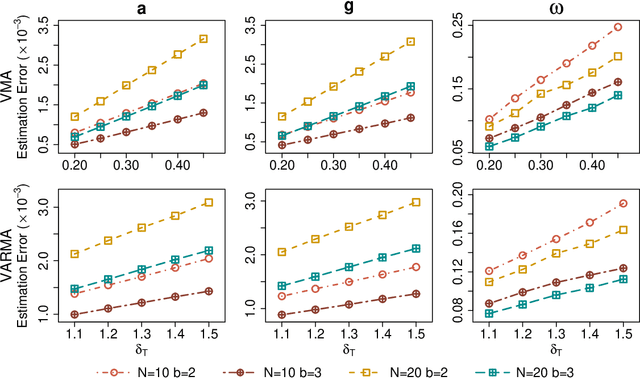
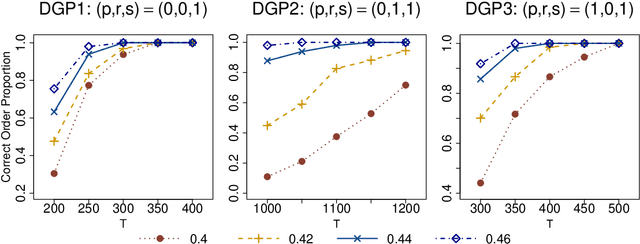
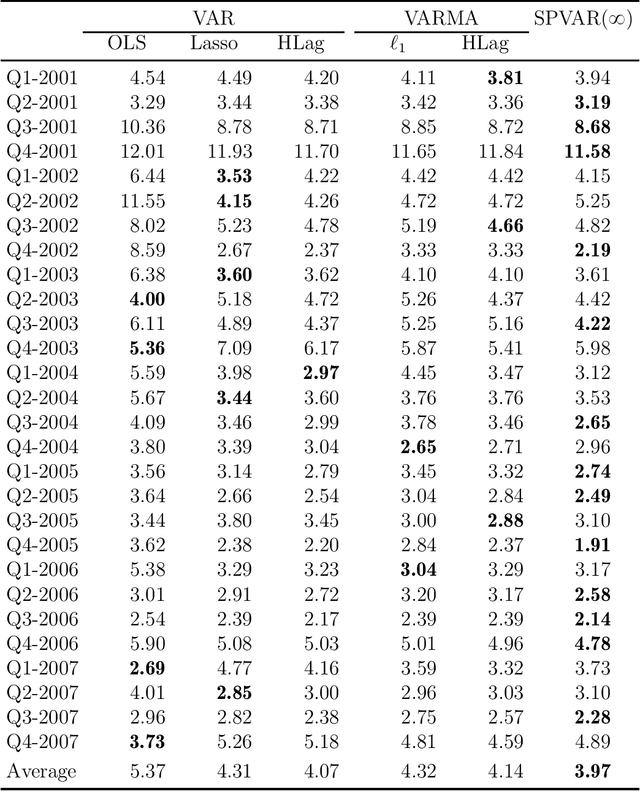
Abstract:As a special infinite-order vector autoregressive (VAR) model, the vector autoregressive moving average (VARMA) model can capture much richer temporal patterns than the widely used finite-order VAR model. However, its practicality has long been hindered by its non-identifiability, computational intractability, and relative difficulty of interpretation. This paper introduces a novel infinite-order VAR model which, with only a little sacrifice of generality, inherits the essential temporal patterns of the VARMA model but avoids all of the above drawbacks. As another attractive feature, the temporal and cross-sectional dependence structures of this model can be interpreted separately, since they are characterized by different sets of parameters. For high-dimensional time series, this separation motivates us to impose sparsity on the parameters determining the cross-sectional dependence. As a result, greater statistical efficiency and interpretability can be achieved, while no loss of temporal information is incurred by the imposed sparsity. We introduce an $\ell_1$-regularized estimator for the proposed model and derive the corresponding nonasymptotic error bounds. An efficient block coordinate descent algorithm and a consistent model order selection method are developed. The merit of the proposed approach is supported by simulation studies and a real-world macroeconomic data analysis.
A New Measure of Model Redundancy for Compressed Convolutional Neural Networks
Dec 09, 2021
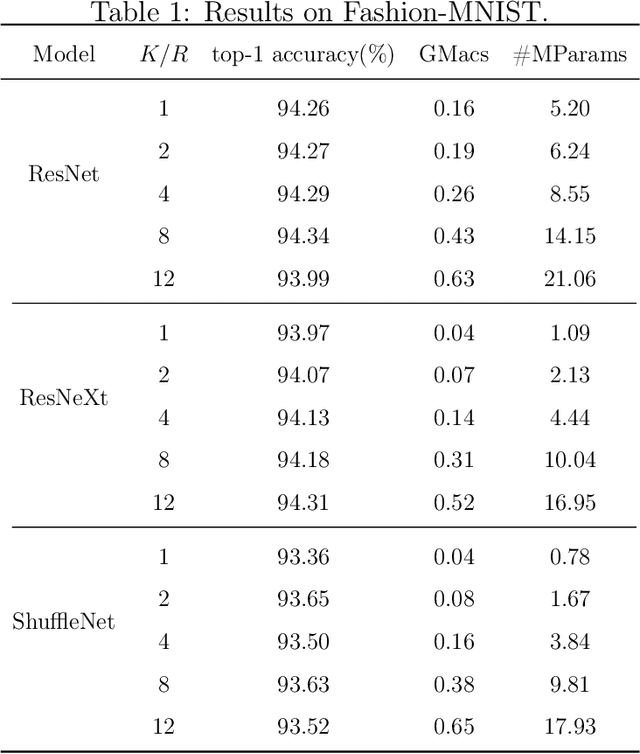
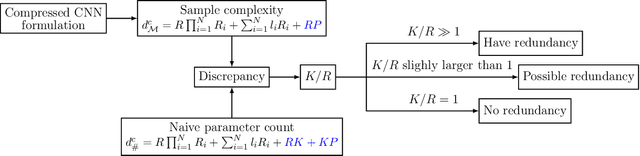
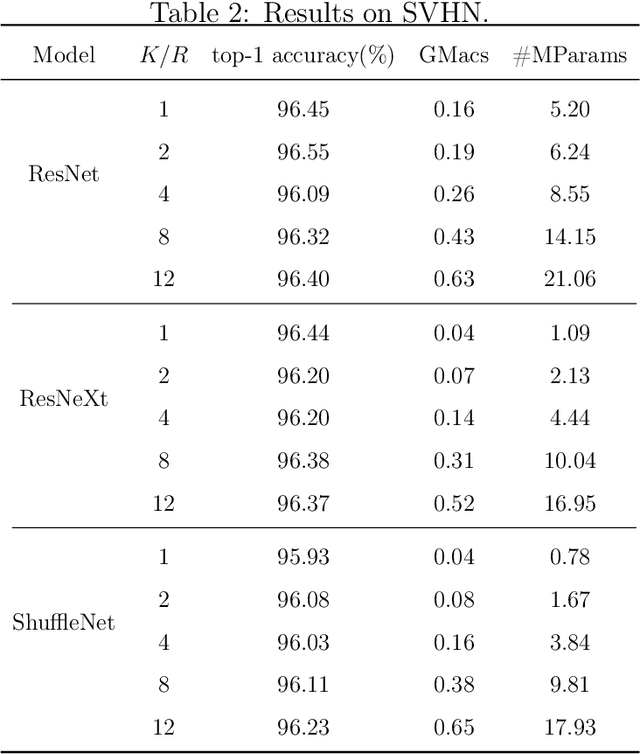
Abstract:While recently many designs have been proposed to improve the model efficiency of convolutional neural networks (CNNs) on a fixed resource budget, theoretical understanding of these designs is still conspicuously lacking. This paper aims to provide a new framework for answering the question: Is there still any remaining model redundancy in a compressed CNN? We begin by developing a general statistical formulation of CNNs and compressed CNNs via the tensor decomposition, such that the weights across layers can be summarized into a single tensor. Then, through a rigorous sample complexity analysis, we reveal an important discrepancy between the derived sample complexity and the naive parameter counting, which serves as a direct indicator of the model redundancy. Motivated by this finding, we introduce a new model redundancy measure for compressed CNNs, called the $K/R$ ratio, which further allows for nonlinear activations. The usefulness of this new measure is supported by ablation studies on popular block designs and datasets.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge