A New Measure of Model Redundancy for Compressed Convolutional Neural Networks
Paper and Code
Dec 09, 2021
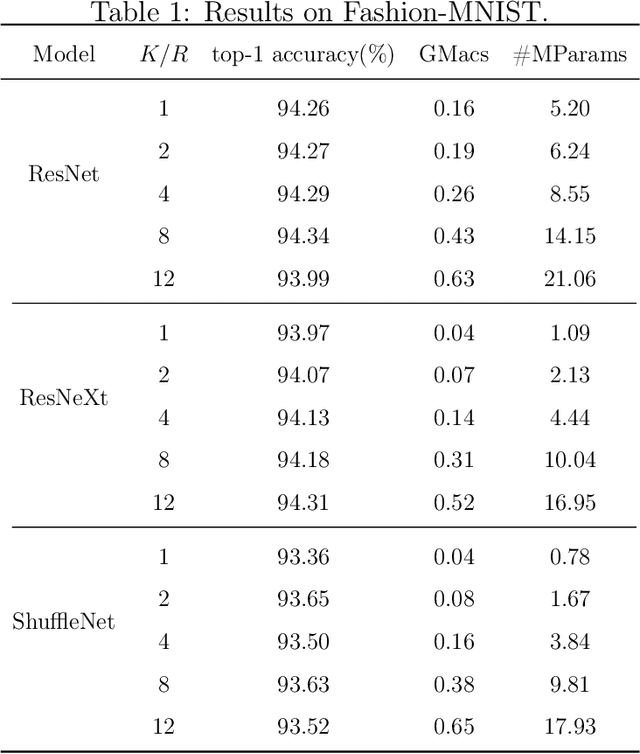
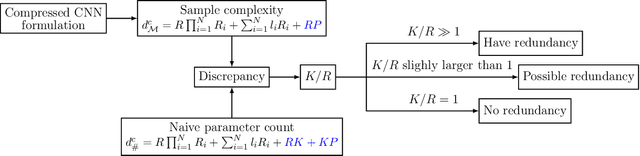
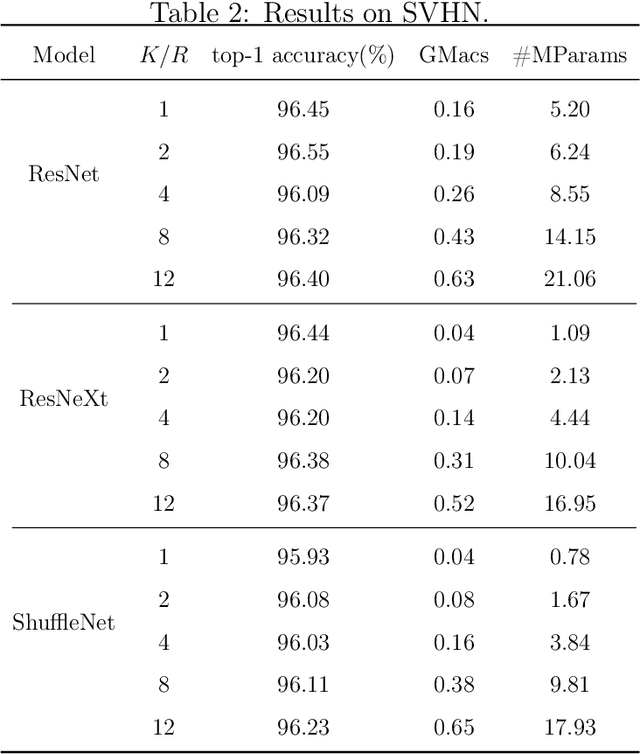
While recently many designs have been proposed to improve the model efficiency of convolutional neural networks (CNNs) on a fixed resource budget, theoretical understanding of these designs is still conspicuously lacking. This paper aims to provide a new framework for answering the question: Is there still any remaining model redundancy in a compressed CNN? We begin by developing a general statistical formulation of CNNs and compressed CNNs via the tensor decomposition, such that the weights across layers can be summarized into a single tensor. Then, through a rigorous sample complexity analysis, we reveal an important discrepancy between the derived sample complexity and the naive parameter counting, which serves as a direct indicator of the model redundancy. Motivated by this finding, we introduce a new model redundancy measure for compressed CNNs, called the $K/R$ ratio, which further allows for nonlinear activations. The usefulness of this new measure is supported by ablation studies on popular block designs and datasets.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge