Machine learning for modelling unstructured grid data in computational physics: a review

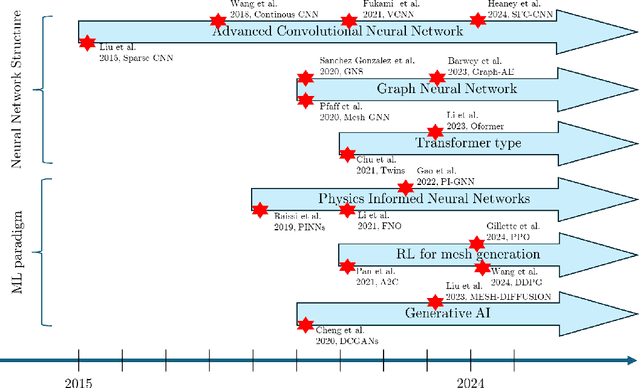
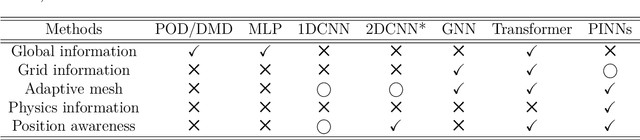
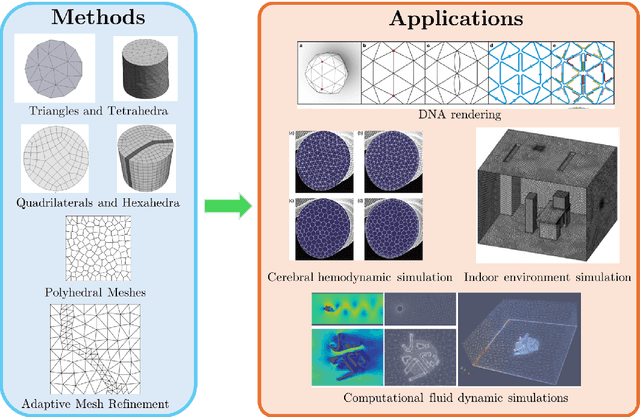
Unstructured grid data are essential for modelling complex geometries and dynamics in computational physics. Yet, their inherent irregularity presents significant challenges for conventional machine learning (ML) techniques. This paper provides a comprehensive review of advanced ML methodologies designed to handle unstructured grid data in high-dimensional dynamical systems. Key approaches discussed include graph neural networks, transformer models with spatial attention mechanisms, interpolation-integrated ML methods, and meshless techniques such as physics-informed neural networks. These methodologies have proven effective across diverse fields, including fluid dynamics and environmental simulations. This review is intended as a guidebook for computational scientists seeking to apply ML approaches to unstructured grid data in their domains, as well as for ML researchers looking to address challenges in computational physics. It places special focus on how ML methods can overcome the inherent limitations of traditional numerical techniques and, conversely, how insights from computational physics can inform ML development. To support benchmarking, this review also provides a summary of open-access datasets of unstructured grid data in computational physics. Finally, emerging directions such as generative models with unstructured data, reinforcement learning for mesh generation, and hybrid physics-data-driven paradigms are discussed to inspire future advancements in this evolving field.

BAG: Body-Aligned 3D Wearable Asset Generation

While recent advancements have shown remarkable progress in general 3D shape generation models, the challenge of leveraging these approaches to automatically generate wearable 3D assets remains unexplored. To this end, we present BAG, a Body-aligned Asset Generation method to output 3D wearable asset that can be automatically dressed on given 3D human bodies. This is achived by controlling the 3D generation process using human body shape and pose information. Specifically, we first build a general single-image to consistent multiview image diffusion model, and train it on the large Objaverse dataset to achieve diversity and generalizability. Then we train a Controlnet to guide the multiview generator to produce body-aligned multiview images. The control signal utilizes the multiview 2D projections of the target human body, where pixel values represent the XYZ coordinates of the body surface in a canonical space. The body-conditioned multiview diffusion generates body-aligned multiview images, which are then fed into a native 3D diffusion model to produce the 3D shape of the asset. Finally, by recovering the similarity transformation using multiview silhouette supervision and addressing asset-body penetration with physics simulators, the 3D asset can be accurately fitted onto the target human body. Experimental results demonstrate significant advantages over existing methods in terms of image prompt-following capability, shape diversity, and shape quality. Our project page is available at https://bag-3d.github.io/.

PhyCAGE: Physically Plausible Compositional 3D Asset Generation from a Single Image

We present PhyCAGE, the first approach for physically plausible compositional 3D asset generation from a single image. Given an input image, we first generate consistent multi-view images for components of the assets. These images are then fitted with 3D Gaussian Splatting representations. To ensure that the Gaussians representing objects are physically compatible with each other, we introduce a Physical Simulation-Enhanced Score Distillation Sampling (PSE-SDS) technique to further optimize the positions of the Gaussians. It is achieved by setting the gradient of the SDS loss as the initial velocity of the physical simulation, allowing the simulator to act as a physics-guided optimizer that progressively corrects the Gaussians' positions to a physically compatible state. Experimental results demonstrate that the proposed method can generate physically plausible compositional 3D assets given a single image.

Towards Universal Mesh Movement Networks

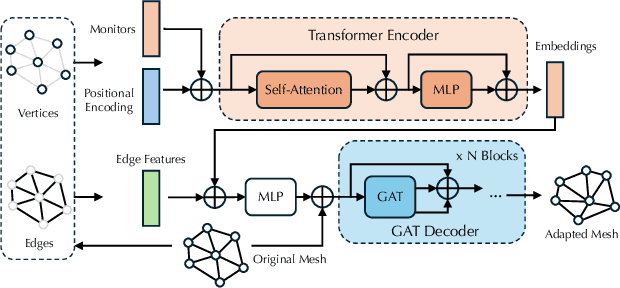
Solving complex Partial Differential Equations (PDEs) accurately and efficiently is an essential and challenging problem in all scientific and engineering disciplines. Mesh movement methods provide the capability to improve the accuracy of the numerical solution without increasing the overall mesh degree of freedom count. Conventional sophisticated mesh movement methods are extremely expensive and struggle to handle scenarios with complex boundary geometries. However, existing learning-based methods require re-training from scratch given a different PDE type or boundary geometry, which limits their applicability, and also often suffer from robustness issues in the form of inverted elements. In this paper, we introduce the Universal Mesh Movement Network (UM2N), which -- once trained -- can be applied in a non-intrusive, zero-shot manner to move meshes with different size distributions and structures, for solvers applicable to different PDE types and boundary geometries. UM2N consists of a Graph Transformer (GT) encoder for extracting features and a Graph Attention Network (GAT) based decoder for moving the mesh. We evaluate our method on advection and Navier-Stokes based examples, as well as a real-world tsunami simulation case. Our method outperforms existing learning-based mesh movement methods in terms of the benchmarks described above. In comparison to the conventional sophisticated Monge-Amp\`ere PDE-solver based method, our approach not only significantly accelerates mesh movement, but also proves effective in scenarios where the conventional method fails. Our project page is at https://erizmr.github.io/UM2N/.

End-to-end Wind Turbine Wake Modelling with Deep Graph Representation Learning

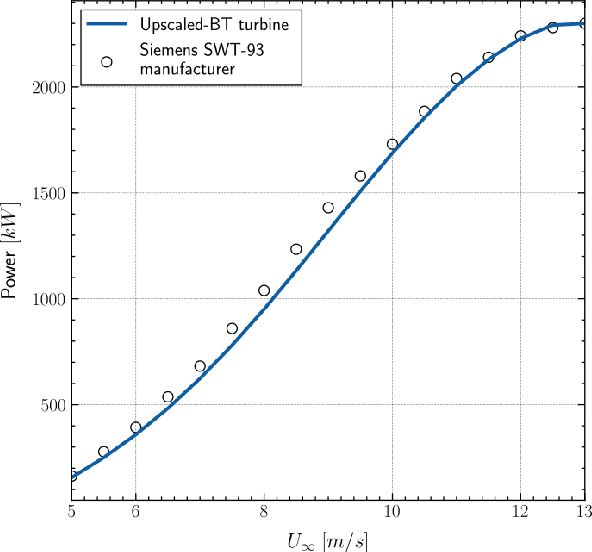
Wind turbine wake modelling is of crucial importance to accurate resource assessment, to layout optimisation, and to the operational control of wind farms. This work proposes a surrogate model for the representation of wind turbine wakes based on a state-of-the-art graph representation learning method termed a graph neural network. The proposed end-to-end deep learning model operates directly on unstructured meshes and has been validated against high-fidelity data, demonstrating its ability to rapidly make accurate 3D flow field predictions for various inlet conditions and turbine yaw angles. The specific graph neural network model employed here is shown to generalise well to unseen data and is less sensitive to over-smoothing compared to common graph neural networks. A case study based upon a real world wind farm further demonstrates the capability of the proposed approach to predict farm scale power generation. Moreover, the proposed graph neural network framework is flexible and highly generic and as formulated here can be applied to any steady state computational fluid dynamics simulations on unstructured meshes.

E2N: Error Estimation Networks for Goal-Oriented Mesh Adaptation

Given a partial differential equation (PDE), goal-oriented error estimation allows us to understand how errors in a diagnostic quantity of interest (QoI), or goal, occur and accumulate in a numerical approximation, for example using the finite element method. By decomposing the error estimates into contributions from individual elements, it is possible to formulate adaptation methods, which modify the mesh with the objective of minimising the resulting QoI error. However, the standard error estimate formulation involves the true adjoint solution, which is unknown in practice. As such, it is common practice to approximate it with an 'enriched' approximation (e.g. in a higher order space or on a refined mesh). Doing so generally results in a significant increase in computational cost, which can be a bottleneck compromising the competitiveness of (goal-oriented) adaptive simulations. The central idea of this paper is to develop a "data-driven" goal-oriented mesh adaptation approach through the selective replacement of the expensive error estimation step with an appropriately configured and trained neural network. In doing so, the error estimator may be obtained without even constructing the enriched spaces. An element-by-element construction is employed here, whereby local values of various parameters related to the mesh geometry and underlying problem physics are taken as inputs, and the corresponding contribution to the error estimator is taken as output. We demonstrate that this approach is able to obtain the same accuracy with a reduced computational cost, for adaptive mesh test cases related to flow around tidal turbines, which interact via their downstream wakes, and where the overall power output of the farm is taken as the QoI. Moreover, we demonstrate that the element-by-element approach implies reasonably low training costs.

Learning to Estimate and Refine Fluid Motion with Physical Dynamics

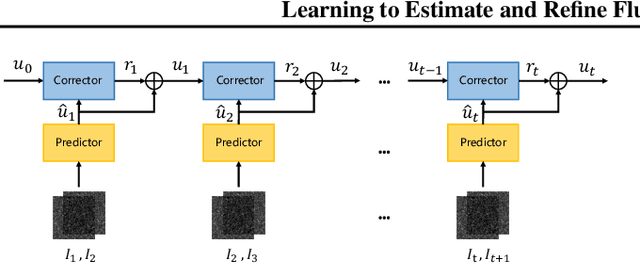
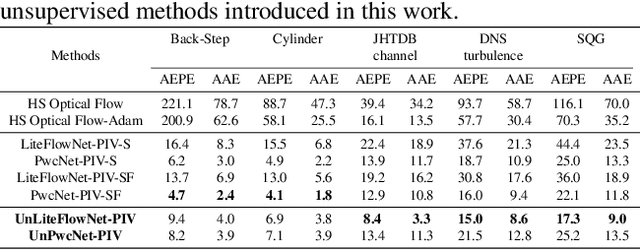
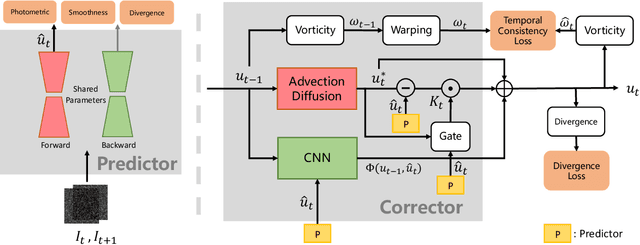
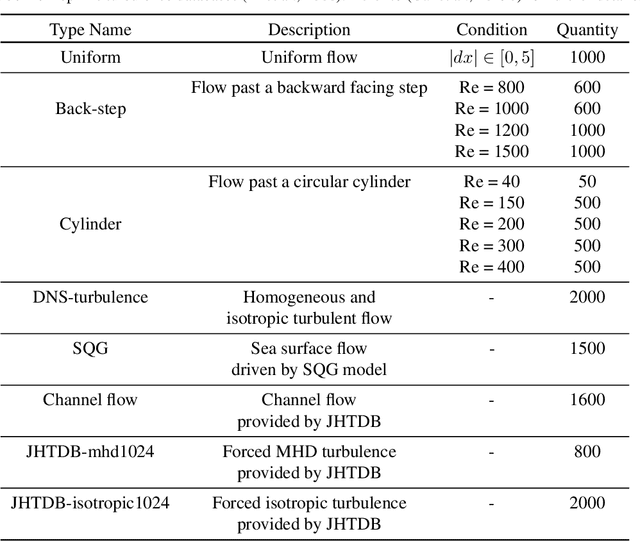
Extracting information on fluid motion directly from images is challenging. Fluid flow represents a complex dynamic system governed by the Navier-Stokes equations. General optical flow methods are typically designed for rigid body motion, and thus struggle if applied to fluid motion estimation directly. Further, optical flow methods only focus on two consecutive frames without utilising historical temporal information, while the fluid motion (velocity field) can be considered a continuous trajectory constrained by time-dependent partial differential equations (PDEs). This discrepancy has the potential to induce physically inconsistent estimations. Here we propose an unsupervised learning based prediction-correction scheme for fluid flow estimation. An estimate is first given by a PDE-constrained optical flow predictor, which is then refined by a physical based corrector. The proposed approach outperforms optical flow methods and shows competitive results compared to existing supervised learning based methods on a benchmark dataset. Furthermore, the proposed approach can generalize to complex real-world fluid scenarios where ground truth information is effectively unknowable. Finally, experiments demonstrate that the physical corrector can refine flow estimates by mimicking the operator splitting method commonly utilised in fluid dynamical simulation.

Complex Locomotion Skill Learning via Differentiable Physics

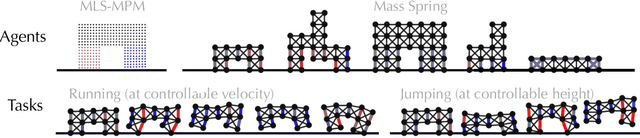
Differentiable physics enables efficient gradient-based optimizations of neural network (NN) controllers. However, existing work typically only delivers NN controllers with limited capability and generalizability. We present a practical learning framework that outputs unified NN controllers capable of tasks with significantly improved complexity and diversity. To systematically improve training robustness and efficiency, we investigated a suite of improvements over the baseline approach, including periodic activation functions, and tailored loss functions. In addition, we find our adoption of batching and an Adam optimizer effective in training complex locomotion tasks. We evaluate our framework on differentiable mass-spring and material point method (MPM) simulations, with challenging locomotion tasks and multiple robot designs. Experiments show that our learning framework, based on differentiable physics, delivers better results than reinforcement learning and converges much faster. We demonstrate that users can interactively control soft robot locomotion and switch among multiple goals with specified velocity, height, and direction instructions using a unified NN controller trained in our system.

M2N: Mesh Movement Networks for PDE Solvers

Mainstream numerical Partial Differential Equation (PDE) solvers require discretizing the physical domain using a mesh. Mesh movement methods aim to improve the accuracy of the numerical solution by increasing mesh resolution where the solution is not well-resolved, whilst reducing unnecessary resolution elsewhere. However, mesh movement methods, such as the Monge-Ampere method, require the solution of auxiliary equations, which can be extremely expensive especially when the mesh is adapted frequently. In this paper, we propose to our best knowledge the first learning-based end-to-end mesh movement framework for PDE solvers. Key requirements of learning-based mesh movement methods are alleviating mesh tangling, boundary consistency, and generalization to mesh with different resolutions. To achieve these goals, we introduce the neural spline model and the graph attention network (GAT) into our models respectively. While the Neural-Spline based model provides more flexibility for large deformation, the GAT based model can handle domains with more complicated shapes and is better at performing delicate local deformation. We validate our methods on stationary and time-dependent, linear and non-linear equations, as well as regularly and irregularly shaped domains. Compared to the traditional Monge-Ampere method, our approach can greatly accelerate the mesh adaptation process, whilst achieving comparable numerical error reduction.

Aesthetic Photo Collage with Deep Reinforcement Learning

Photo collage aims to automatically arrange multiple photos on a given canvas with high aesthetic quality. Existing methods are based mainly on handcrafted feature optimization, which cannot adequately capture high-level human aesthetic senses. Deep learning provides a promising way, but owing to the complexity of collage and lack of training data, a solution has yet to be found. In this paper, we propose a novel pipeline for automatic generation of aspect ratio specified collage and the reinforcement learning technique is introduced in collage for the first time. Inspired by manual collages, we model the collage generation as sequential decision process to adjust spatial positions, orientation angles, placement order and the global layout. To instruct the agent to improve both the overall layout and local details, the reward function is specially designed for collage, considering subjective and objective factors. To overcome the lack of training data, we pretrain our deep aesthetic network on a large scale image aesthetic dataset (CPC) for general aesthetic feature extraction and propose an attention fusion module for structural collage feature representation. We test our model against competing methods on two movie datasets and our results outperform others in aesthetic quality evaluation. Further user study is also conducted to demonstrate the effectiveness.