Sim-to-Real of Soft Robots with Learned Residual Physics

Accurately modeling soft robots in simulation is computationally expensive and commonly falls short of representing the real world. This well-known discrepancy, known as the sim-to-real gap, can have several causes, such as coarsely approximated geometry and material models, manufacturing defects, viscoelasticity and plasticity, and hysteresis effects. Residual physics networks learn from real-world data to augment a discrepant model and bring it closer to reality. Here, we present a residual physics method for modeling soft robots with large degrees of freedom. We train neural networks to learn a residual term -- the modeling error between simulated and physical systems. Concretely, the residual term is a force applied on the whole simulated mesh, while real position data is collected with only sparse motion markers. The physical prior of the analytical simulation provides a starting point for the residual network, and the combined model is more informed than if physics were learned tabula rasa. We demonstrate our method on 1) a silicone elastomeric beam and 2) a soft pneumatic arm with hard-to-model, anisotropic fiber reinforcements. Our method outperforms traditional system identification up to 60%. We show that residual physics need not be limited to low degrees of freedom but can effectively bridge the sim-to-real gap for high dimensional systems.

M2N: Mesh Movement Networks for PDE Solvers

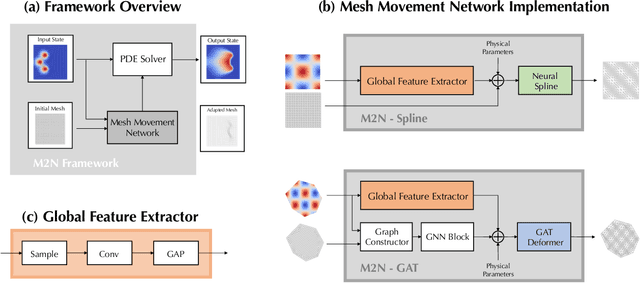
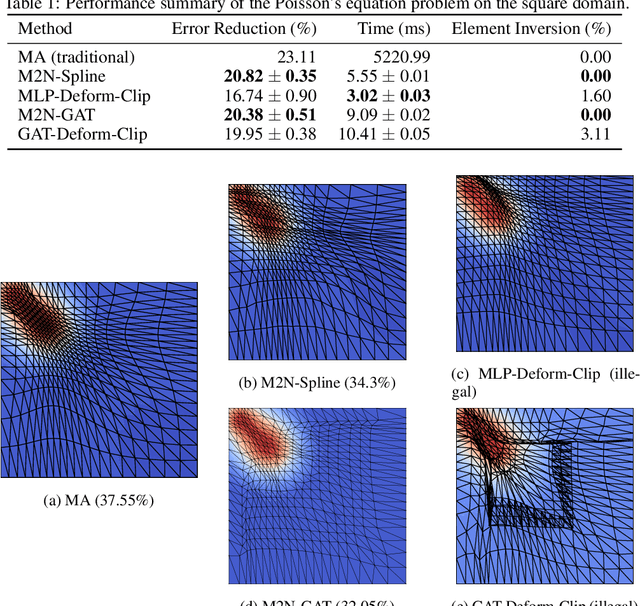
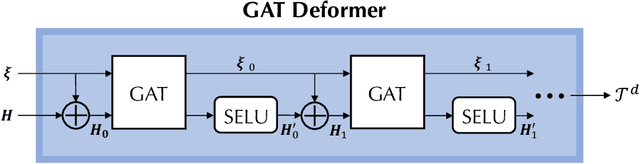
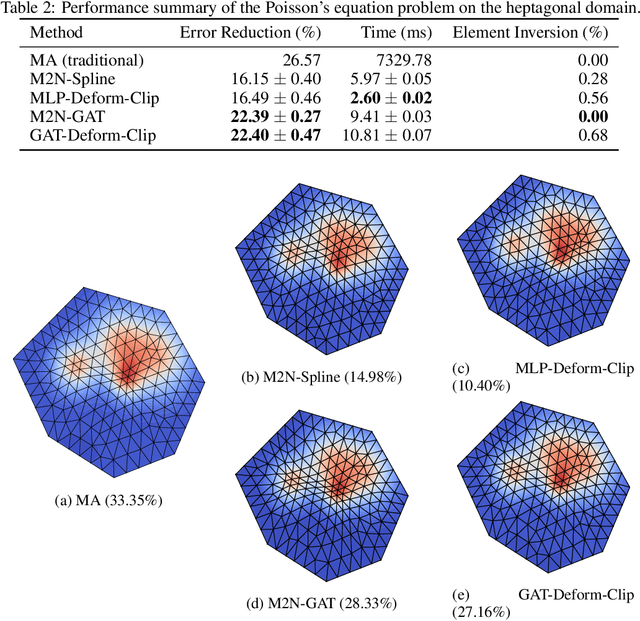
Mainstream numerical Partial Differential Equation (PDE) solvers require discretizing the physical domain using a mesh. Mesh movement methods aim to improve the accuracy of the numerical solution by increasing mesh resolution where the solution is not well-resolved, whilst reducing unnecessary resolution elsewhere. However, mesh movement methods, such as the Monge-Ampere method, require the solution of auxiliary equations, which can be extremely expensive especially when the mesh is adapted frequently. In this paper, we propose to our best knowledge the first learning-based end-to-end mesh movement framework for PDE solvers. Key requirements of learning-based mesh movement methods are alleviating mesh tangling, boundary consistency, and generalization to mesh with different resolutions. To achieve these goals, we introduce the neural spline model and the graph attention network (GAT) into our models respectively. While the Neural-Spline based model provides more flexibility for large deformation, the GAT based model can handle domains with more complicated shapes and is better at performing delicate local deformation. We validate our methods on stationary and time-dependent, linear and non-linear equations, as well as regularly and irregularly shaped domains. Compared to the traditional Monge-Ampere method, our approach can greatly accelerate the mesh adaptation process, whilst achieving comparable numerical error reduction.