LightAgent: Production-level Open-source Agentic AI Framework

With the rapid advancement of large language models (LLMs), Multi-agent Systems (MAS) have achieved significant progress in various application scenarios. However, substantial challenges remain in designing versatile, robust, and efficient platforms for agent deployment. To address these limitations, we propose \textbf{LightAgent}, a lightweight yet powerful agentic framework, effectively resolving the trade-off between flexibility and simplicity found in existing frameworks. LightAgent integrates core functionalities such as Memory (mem0), Tools, and Tree of Thought (ToT), while maintaining an extremely lightweight structure. As a fully open-source solution, it seamlessly integrates with mainstream chat platforms, enabling developers to easily build self-learning agents. We have released LightAgent at \href{https://github.com/wxai-space/LightAgent}{https://github.com/wxai-space/LightAgent}

Effect Decomposition of Functional-Output Computer Experiments via Orthogonal Additive Gaussian Processes

Functional ANOVA (FANOVA) is a widely used variance-based sensitivity analysis tool. However, studies on functional-output FANOVA remain relatively scarce, especially for black-box computer experiments, which often involve complex and nonlinear functional-output relationships with unknown data distribution. Conventional approaches often rely on predefined basis functions or parametric structures that lack the flexibility to capture complex nonlinear relationships. Additionally, strong assumptions about the underlying data distributions further limit their ability to achieve a data-driven orthogonal effect decomposition. To address these challenges, this study proposes a functional-output orthogonal additive Gaussian process (FOAGP) to efficiently perform the data-driven orthogonal effect decomposition. By enforcing a conditional orthogonality constraint on the separable prior process, the proposed functional-output orthogonal additive kernel enables data-driven orthogonality without requiring prior distributional assumptions. The FOAGP framework also provides analytical formulations for local Sobol' indices and expected conditional variance sensitivity indices, enabling comprehensive sensitivity analysis by capturing both global and local effect significance. Validation through two simulation studies and a real case study on fuselage shape control confirms the model's effectiveness in orthogonal effect decomposition and variance decomposition, demonstrating its practical value in engineering applications.

Incentivizing Truthful Language Models via Peer Elicitation Games

Large Language Models (LLMs) have demonstrated strong generative capabilities but remain prone to inconsistencies and hallucinations. We introduce Peer Elicitation Games (PEG), a training-free, game-theoretic framework for aligning LLMs through a peer elicitation mechanism involving a generator and multiple discriminators instantiated from distinct base models. Discriminators interact in a peer evaluation setting, where rewards are computed using a determinant-based mutual information score that provably incentivizes truthful reporting without requiring ground-truth labels. We establish theoretical guarantees showing that each agent, via online learning, achieves sublinear regret in the sense their cumulative performance approaches that of the best fixed truthful strategy in hindsight. Moreover, we prove last-iterate convergence to a truthful Nash equilibrium, ensuring that the actual policies used by agents converge to stable and truthful behavior over time. Empirical evaluations across multiple benchmarks demonstrate significant improvements in factual accuracy. These results position PEG as a practical approach for eliciting truthful behavior from LLMs without supervision or fine-tuning.

Learn then Decide: A Learning Approach for Designing Data Marketplaces

As data marketplaces become increasingly central to the digital economy, it is crucial to design efficient pricing mechanisms that optimize revenue while ensuring fair and adaptive pricing. We introduce the Maximum Auction-to-Posted Price (MAPP) mechanism, a novel two-stage approach that first estimates the bidders' value distribution through auctions and then determines the optimal posted price based on the learned distribution. We establish that MAPP is individually rational and incentive-compatible, ensuring truthful bidding while balancing revenue maximization with minimal price discrimination. MAPP achieves a regret of $O_p(n^{-1})$ when incorporating historical bid data, where $n$ is the number of bids in the current round. It outperforms existing methods while imposing weaker distributional assumptions. For sequential dataset sales over $T$ rounds, we propose an online MAPP mechanism that dynamically adjusts pricing across datasets with varying value distributions. Our approach achieves no-regret learning, with the average cumulative regret converging at a rate of $O_p(T^{-1/2}(\log T)^2)$. We validate the effectiveness of MAPP through simulations and real-world data from the FCC AWS-3 spectrum auction.

Fairness-aware organ exchange and kidney paired donation

The kidney paired donation (KPD) program provides an innovative solution to overcome incompatibility challenges in kidney transplants by matching incompatible donor-patient pairs and facilitating kidney exchanges. To address unequal access to transplant opportunities, there are two widely used fairness criteria: group fairness and individual fairness. However, these criteria do not consider protected patient features, which refer to characteristics legally or ethically recognized as needing protection from discrimination, such as race and gender. Motivated by the calibration principle in machine learning, we introduce a new fairness criterion: the matching outcome should be conditionally independent of the protected feature, given the sensitization level. We integrate this fairness criterion as a constraint within the KPD optimization framework and propose a computationally efficient solution. Theoretically, we analyze the associated price of fairness using random graph models. Empirically, we compare our fairness criterion with group fairness and individual fairness through both simulations and a real-data example.

Dynamic Online Recommendation for Two-Sided Market with Bayesian Incentive Compatibility

Recommender systems play a crucial role in internet economies by connecting users with relevant products or services. However, designing effective recommender systems faces two key challenges: (1) the exploration-exploitation tradeoff in balancing new product exploration against exploiting known preferences, and (2) dynamic incentive compatibility in accounting for users' self-interested behaviors and heterogeneous preferences. This paper formalizes these challenges into a Dynamic Bayesian Incentive-Compatible Recommendation Protocol (DBICRP). To address the DBICRP, we propose a two-stage algorithm (RCB) that integrates incentivized exploration with an efficient offline learning component for exploitation. In the first stage, our algorithm explores available products while maintaining dynamic incentive compatibility to determine sufficient sample sizes. The second stage employs inverse proportional gap sampling integrated with an arbitrary machine learning method to ensure sublinear regret. Theoretically, we prove that RCB achieves $O(\sqrt{KdT})$ regret and satisfies Bayesian incentive compatibility (BIC) under a Gaussian prior assumption. Empirically, we validate RCB's strong incentive gain, sublinear regret, and robustness through simulations and a real-world application on personalized warfarin dosing. Our work provides a principled approach for incentive-aware recommendation in online preference learning settings.

Conformal Online Auction Design

This paper proposes the conformal online auction design (COAD), a novel mechanism for maximizing revenue in online auctions by quantifying the uncertainty in bidders' values without relying on assumptions about value distributions. COAD incorporates both the bidder and item features and leverages historical data to provide an incentive-compatible mechanism for online auctions. Unlike traditional methods for online auctions, COAD employs a distribution-free, prediction interval-based approach using conformal prediction techniques. This novel approach ensures that the expected revenue from our mechanism can achieve at least a constant fraction of the revenue generated by the optimal mechanism. Additionally, COAD admits the use of a broad array of modern machine-learning methods, including random forests, kernel methods, and deep neural nets, for predicting bidders' values. It ensures revenue performance under any finite sample of historical data. Moreover, COAD introduces bidder-specific reserve prices based on the lower confidence bounds of bidders' valuations, which is different from the uniform reserve prices commonly used in the literature. We validate our theoretical predictions through extensive simulations and a real-data application. All code for using COAD and reproducing results is made available on GitHub.

An ODE Model for Dynamic Matching in Heterogeneous Networks

We study the problem of dynamic matching in heterogeneous networks, where agents are subject to compatibility restrictions and stochastic arrival and departure times. In particular, we consider networks with one type of easy-to-match agents and multiple types of hard-to-match agents, each subject to its own compatibility constraints. Such a setting arises in many real-world applications, including kidney exchange programs and carpooling platforms. We introduce a novel approach to modeling dynamic matching by establishing the ordinary differential equation (ODE) model, which offers a new perspective for evaluating various matching algorithms. We study two algorithms, namely the Greedy and Patient Algorithms, where both algorithms prioritize matching compatible hard-to-match agents over easy-to-match agents in heterogeneous networks. Our results demonstrate the trade-off between the conflicting goals of matching agents quickly and optimally, offering insights into the design of real-world dynamic matching systems. We provide simulations and a real-world case study using data from the Organ Procurement and Transplantation Network to validate theoretical predictions.

Robust multi-item auction design using statistical learning: Overcoming uncertainty in bidders' types distributions

This paper presents a novel mechanism design for multi-item auction settings with uncertain bidders' type distributions. Our proposed approach utilizes nonparametric density estimation to accurately estimate bidders' types from historical bids, and is built upon the Vickrey-Clarke-Groves (VCG) mechanism, ensuring satisfaction of Bayesian incentive compatibility (BIC) and $\delta$-individual rationality (IR). To further enhance the efficiency of our mechanism, we introduce two novel strategies for query reduction: a filtering method that screens potential winners' value regions within the confidence intervals generated by our estimated distribution, and a classification strategy that designates the lower bound of an interval as the estimated type when the length is below a threshold value. Simulation experiments conducted on both small-scale and large-scale data demonstrate that our mechanism consistently outperforms existing methods in terms of revenue maximization and query reduction, particularly in large-scale scenarios. This makes our proposed mechanism a highly desirable and effective option for sellers in the realm of multi-item auctions.

Double Matching Under Complementary Preferences

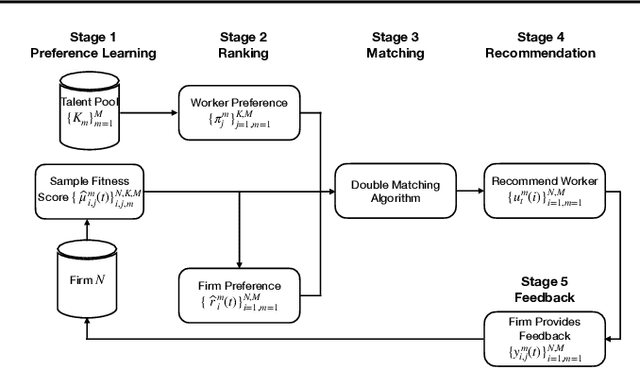
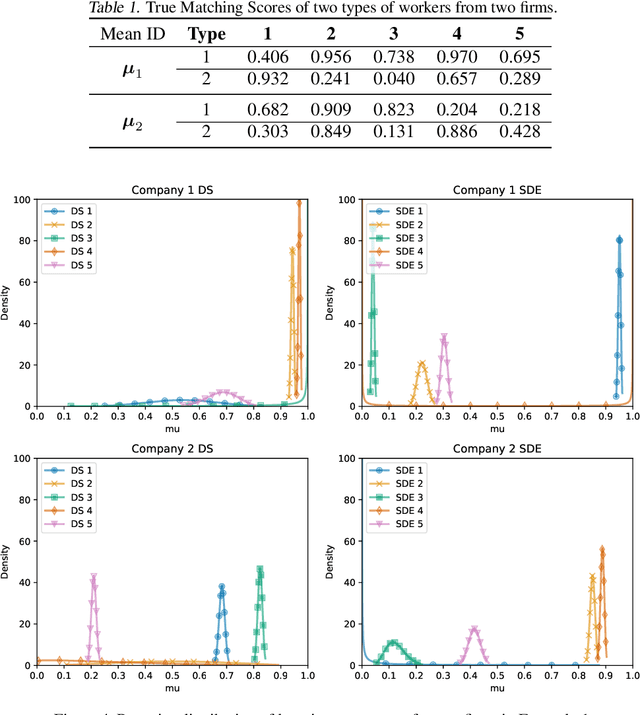
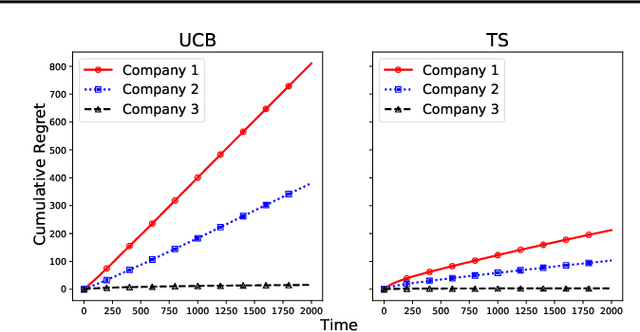
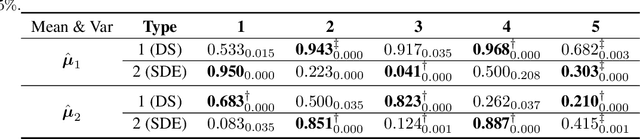
In this paper, we propose a new algorithm for addressing the problem of matching markets with complementary preferences, where agents' preferences are unknown a priori and must be learned from data. The presence of complementary preferences can lead to instability in the matching process, making this problem challenging to solve. To overcome this challenge, we formulate the problem as a bandit learning framework and propose the Multi-agent Multi-type Thompson Sampling (MMTS) algorithm. The algorithm combines the strengths of Thompson Sampling for exploration with a double matching technique to achieve a stable matching outcome. Our theoretical analysis demonstrates the effectiveness of MMTS as it is able to achieve stability at every matching step, satisfies the incentive-compatibility property, and has a sublinear Bayesian regret over time. Our approach provides a useful method for addressing complementary preferences in real-world scenarios.