Incentive-Aware Recommender Systems in Two-Sided Markets

Online platforms in the Internet Economy commonly incorporate recommender systems that recommend arms (e.g., products) to agents (e.g., users). In such platforms, a myopic agent has a natural incentive to exploit, by choosing the best product given the current information rather than to explore various alternatives to collect information that will be used for other agents. We propose a novel recommender system that respects agents' incentives and enjoys asymptotically optimal performances expressed by the regret in repeated games. We model such an incentive-aware recommender system as a multi-agent bandit problem in a two-sided market which is equipped with an incentive constraint induced by agents' opportunity costs. If the opportunity costs are known to the principal, we show that there exists an incentive-compatible recommendation policy, which pools recommendations across a genuinely good arm and an unknown arm via a randomized and adaptive approach. On the other hand, if the opportunity costs are unknown to the principal, we propose a policy that randomly pools recommendations across all arms and uses each arm's cumulative loss as feedback for exploration. We show that both policies also satisfy an ex-post fairness criterion, which protects agents from over-exploitation.

Virtual Vector Machine for Bayesian Online Classification

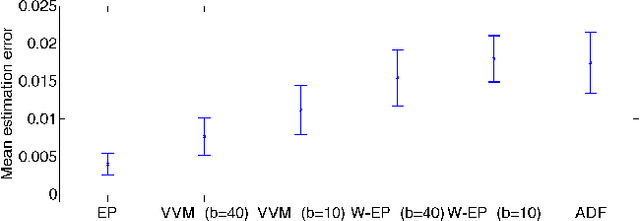
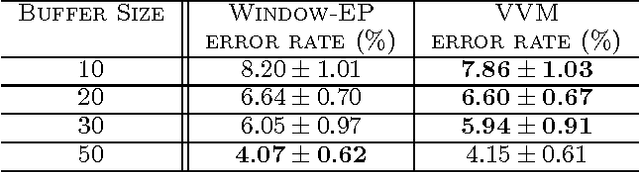
In a typical online learning scenario, a learner is required to process a large data stream using a small memory buffer. Such a requirement is usually in conflict with a learner's primary pursuit of prediction accuracy. To address this dilemma, we introduce a novel Bayesian online classi cation algorithm, called the Virtual Vector Machine. The virtual vector machine allows you to smoothly trade-off prediction accuracy with memory size. The virtual vector machine summarizes the information contained in the preceding data stream by a Gaussian distribution over the classi cation weights plus a constant number of virtual data points. The virtual data points are designed to add extra non-Gaussian information about the classi cation weights. To maintain the constant number of virtual points, the virtual vector machine adds the current real data point into the virtual point set, merges two most similar virtual points into a new virtual point or deletes a virtual point that is far from the decision boundary. The information lost in this process is absorbed into the Gaussian distribution. The extra information provided by the virtual points leads to improved predictive accuracy over previous online classification algorithms.

Sparse-posterior Gaussian Processes for general likelihoods

Gaussian processes (GPs) provide a probabilistic nonparametric representation of functions in regression, classification, and other problems. Unfortunately, exact learning with GPs is intractable for large datasets. A variety of approximate GP methods have been proposed that essentially map the large dataset into a small set of basis points. Among them, two state-of-the-art methods are sparse pseudo-input Gaussian process (SPGP) (Snelson and Ghahramani, 2006) and variablesigma GP (VSGP) Walder et al. (2008), which generalizes SPGP and allows each basis point to have its own length scale. However, VSGP was only derived for regression. In this paper, we propose a new sparse GP framework that uses expectation propagation to directly approximate general GP likelihoods using a sparse and smooth basis. It includes both SPGP and VSGP for regression as special cases. Plus as an EP algorithm, it inherits the ability to process data online. As a particular choice of approximating family, we blur each basis point with a Gaussian distribution that has a full covariance matrix representing the data distribution around that basis point; as a result, we can summarize local data manifold information with a small set of basis points. Our experiments demonstrate that this framework outperforms previous GP classification methods on benchmark datasets in terms of minimizing divergence to the non-sparse GP solution as well as lower misclassification rate.

Sparse matrix-variate Gaussian process blockmodels for network modeling

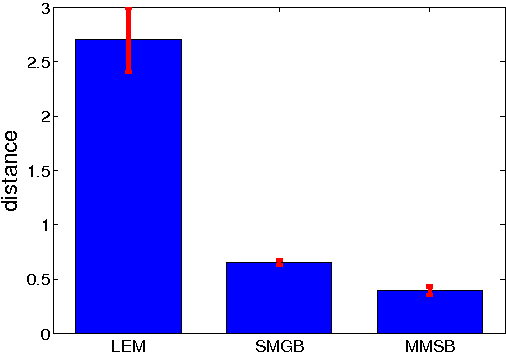
We face network data from various sources, such as protein interactions and online social networks. A critical problem is to model network interactions and identify latent groups of network nodes. This problem is challenging due to many reasons. For example, the network nodes are interdependent instead of independent of each other, and the data are known to be very noisy (e.g., missing edges). To address these challenges, we propose a new relational model for network data, Sparse Matrix-variate Gaussian process Blockmodel (SMGB). Our model generalizes popular bilinear generative models and captures nonlinear network interactions using a matrix-variate Gaussian process with latent membership variables. We also assign sparse prior distributions on the latent membership variables to learn sparse group assignments for individual network nodes. To estimate the latent variables efficiently from data, we develop an efficient variational expectation maximization method. We compared our approaches with several state-of-the-art network models on both synthetic and real-world network datasets. Experimental results demonstrate SMGBs outperform the alternative approaches in terms of discovering latent classes or predicting unknown interactions.

Infinite Tucker Decomposition: Nonparametric Bayesian Models for Multiway Data Analysis

Tensor decomposition is a powerful computational tool for multiway data analysis. Many popular tensor decomposition approaches---such as the Tucker decomposition and CANDECOMP/PARAFAC (CP)---amount to multi-linear factorization. They are insufficient to model (i) complex interactions between data entities, (ii) various data types (e.g. missing data and binary data), and (iii) noisy observations and outliers. To address these issues, we propose tensor-variate latent nonparametric Bayesian models, coupled with efficient inference methods, for multiway data analysis. We name these models InfTucker. Using these InfTucker, we conduct Tucker decomposition in an infinite feature space. Unlike classical tensor decomposition models, our new approaches handle both continuous and binary data in a probabilistic framework. Unlike previous Bayesian models on matrices and tensors, our models are based on latent Gaussian or $t$ processes with nonlinear covariance functions. To efficiently learn the InfTucker from data, we develop a variational inference technique on tensors. Compared with classical implementation, the new technique reduces both time and space complexities by several orders of magnitude. Our experimental results on chemometrics and social network datasets demonstrate that our new models achieved significantly higher prediction accuracy than the most state-of-art tensor decomposition