Sparse matrix-variate Gaussian process blockmodels for network modeling
Paper and Code
Feb 14, 2012
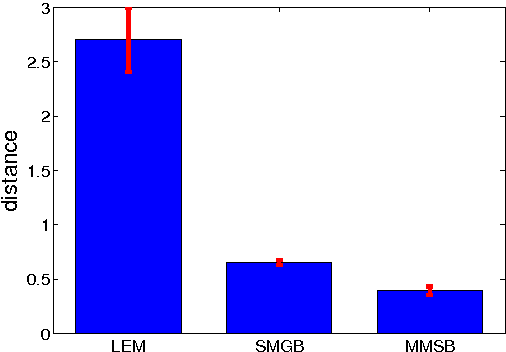


We face network data from various sources, such as protein interactions and online social networks. A critical problem is to model network interactions and identify latent groups of network nodes. This problem is challenging due to many reasons. For example, the network nodes are interdependent instead of independent of each other, and the data are known to be very noisy (e.g., missing edges). To address these challenges, we propose a new relational model for network data, Sparse Matrix-variate Gaussian process Blockmodel (SMGB). Our model generalizes popular bilinear generative models and captures nonlinear network interactions using a matrix-variate Gaussian process with latent membership variables. We also assign sparse prior distributions on the latent membership variables to learn sparse group assignments for individual network nodes. To estimate the latent variables efficiently from data, we develop an efficient variational expectation maximization method. We compared our approaches with several state-of-the-art network models on both synthetic and real-world network datasets. Experimental results demonstrate SMGBs outperform the alternative approaches in terms of discovering latent classes or predicting unknown interactions.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge