Expectation Propagation for approximate Bayesian inference

This paper presents a new deterministic approximation technique in Bayesian networks. This method, "Expectation Propagation", unifies two previous techniques: assumed-density filtering, an extension of the Kalman filter, and loopy belief propagation, an extension of belief propagation in Bayesian networks. All three algorithms try to recover an approximate distribution which is close in KL divergence to the true distribution. Loopy belief propagation, because it propagates exact belief states, is useful for a limited class of belief networks, such as those which are purely discrete. Expectation Propagation approximates the belief states by only retaining certain expectations, such as mean and variance, and iterates until these expectations are consistent throughout the network. This makes it applicable to hybrid networks with discrete and continuous nodes. Expectation Propagation also extends belief propagation in the opposite direction - it can propagate richer belief states that incorporate correlations between nodes. Experiments with Gaussian mixture models show Expectation Propagation to be convincingly better than methods with similar computational cost: Laplace's method, variational Bayes, and Monte Carlo. Expectation Propagation also provides an efficient algorithm for training Bayes point machine classifiers.

Expectation-Propogation for the Generative Aspect Model

The generative aspect model is an extension of the multinomial model for text that allows word probabilities to vary stochastically across documents. Previous results with aspect models have been promising, but hindered by the computational difficulty of carrying out inference and learning. This paper demonstrates that the simple variational methods of Blei et al (2001) can lead to inaccurate inferences and biased learning for the generative aspect model. We develop an alternative approach that leads to higher accuracy at comparable cost. An extension of Expectation-Propagation is used for inference and then embedded in an EM algorithm for learning. Experimental results are presented for both synthetic and real data sets.

Structured Region Graphs: Morphing EP into GBP

GBP and EP are two successful algorithms for approximate probabilistic inference, which are based on different approximation strategies. An open problem in both algorithms has been how to choose an appropriate approximation structure. We introduce 'structured region graphs', a formalism which marries these two strategies, reveals a deep connection between them, and suggests how to choose good approximation structures. In this formalism, each region has an internal structure which defines an exponential family, whose sufficient statistics must be matched by the parent region. Reduction operators on these structures allow conversion between EP and GBP free energies. Thus it is revealed that all EP approximations on discrete variables are special cases of GBP, and conversely that some wellknown GBP approximations, such as overlapping squares, are special cases of EP. Furthermore, region graphs derived from EP have a number of good structural properties, including maxent-normality and overall counting number of one. The result is a convenient framework for producing high-quality approximations with a user-adjustable level of complexity

Virtual Vector Machine for Bayesian Online Classification

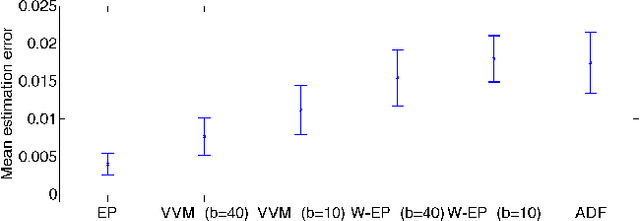
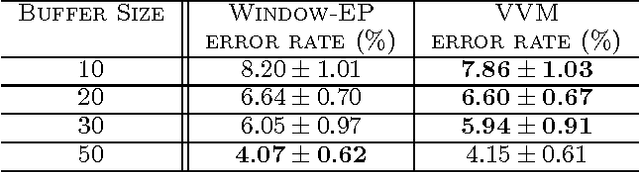
In a typical online learning scenario, a learner is required to process a large data stream using a small memory buffer. Such a requirement is usually in conflict with a learner's primary pursuit of prediction accuracy. To address this dilemma, we introduce a novel Bayesian online classi cation algorithm, called the Virtual Vector Machine. The virtual vector machine allows you to smoothly trade-off prediction accuracy with memory size. The virtual vector machine summarizes the information contained in the preceding data stream by a Gaussian distribution over the classi cation weights plus a constant number of virtual data points. The virtual data points are designed to add extra non-Gaussian information about the classi cation weights. To maintain the constant number of virtual points, the virtual vector machine adds the current real data point into the virtual point set, merges two most similar virtual points into a new virtual point or deletes a virtual point that is far from the decision boundary. The information lost in this process is absorbed into the Gaussian distribution. The extra information provided by the virtual points leads to improved predictive accuracy over previous online classification algorithms.

Sparse-posterior Gaussian Processes for general likelihoods

Gaussian processes (GPs) provide a probabilistic nonparametric representation of functions in regression, classification, and other problems. Unfortunately, exact learning with GPs is intractable for large datasets. A variety of approximate GP methods have been proposed that essentially map the large dataset into a small set of basis points. Among them, two state-of-the-art methods are sparse pseudo-input Gaussian process (SPGP) (Snelson and Ghahramani, 2006) and variablesigma GP (VSGP) Walder et al. (2008), which generalizes SPGP and allows each basis point to have its own length scale. However, VSGP was only derived for regression. In this paper, we propose a new sparse GP framework that uses expectation propagation to directly approximate general GP likelihoods using a sparse and smooth basis. It includes both SPGP and VSGP for regression as special cases. Plus as an EP algorithm, it inherits the ability to process data online. As a particular choice of approximating family, we blur each basis point with a Gaussian distribution that has a full covariance matrix representing the data distribution around that basis point; as a result, we can summarize local data manifold information with a small set of basis points. Our experiments demonstrate that this framework outperforms previous GP classification methods on benchmark datasets in terms of minimizing divergence to the non-sparse GP solution as well as lower misclassification rate.

Variable sigma Gaussian processes: An expectation propagation perspective

Gaussian processes (GPs) provide a probabilistic nonparametric representation of functions in regression, classification, and other problems. Unfortunately, exact learning with GPs is intractable for large datasets. A variety of approximate GP methods have been proposed that essentially map the large dataset into a small set of basis points. The most advanced of these, the variable-sigma GP (VSGP) (Walder et al., 2008), allows each basis point to have its own length scale. However, VSGP was only derived for regression. We describe how VSGP can be applied to classification and other problems, by deriving it as an expectation propagation algorithm. In this view, sparse GP approximations correspond to a KL-projection of the true posterior onto a compact exponential family of GPs. VSGP constitutes one such family, and we show how to enlarge this family to get additional accuracy. In particular, we show that endowing each basis point with its own full covariance matrix provides a significant increase in approximation power.