Dynamic Online Recommendation for Two-Sided Market with Bayesian Incentive Compatibility

Recommender systems play a crucial role in internet economies by connecting users with relevant products or services. However, designing effective recommender systems faces two key challenges: (1) the exploration-exploitation tradeoff in balancing new product exploration against exploiting known preferences, and (2) dynamic incentive compatibility in accounting for users' self-interested behaviors and heterogeneous preferences. This paper formalizes these challenges into a Dynamic Bayesian Incentive-Compatible Recommendation Protocol (DBICRP). To address the DBICRP, we propose a two-stage algorithm (RCB) that integrates incentivized exploration with an efficient offline learning component for exploitation. In the first stage, our algorithm explores available products while maintaining dynamic incentive compatibility to determine sufficient sample sizes. The second stage employs inverse proportional gap sampling integrated with an arbitrary machine learning method to ensure sublinear regret. Theoretically, we prove that RCB achieves $O(\sqrt{KdT})$ regret and satisfies Bayesian incentive compatibility (BIC) under a Gaussian prior assumption. Empirically, we validate RCB's strong incentive gain, sublinear regret, and robustness through simulations and a real-world application on personalized warfarin dosing. Our work provides a principled approach for incentive-aware recommendation in online preference learning settings.

Double Matching Under Complementary Preferences

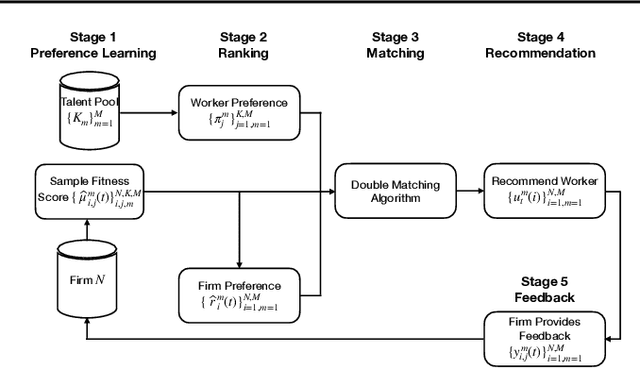
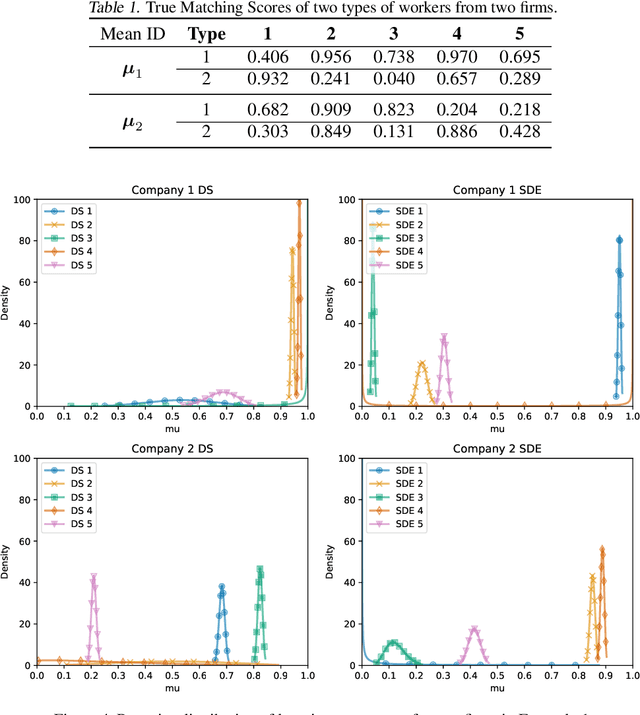
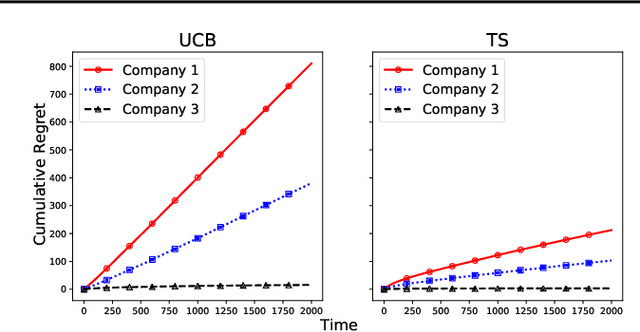
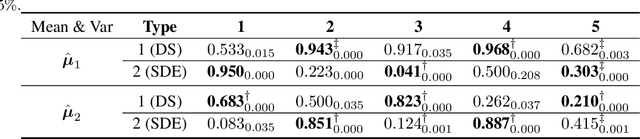
In this paper, we propose a new algorithm for addressing the problem of matching markets with complementary preferences, where agents' preferences are unknown a priori and must be learned from data. The presence of complementary preferences can lead to instability in the matching process, making this problem challenging to solve. To overcome this challenge, we formulate the problem as a bandit learning framework and propose the Multi-agent Multi-type Thompson Sampling (MMTS) algorithm. The algorithm combines the strengths of Thompson Sampling for exploration with a double matching technique to achieve a stable matching outcome. Our theoretical analysis demonstrates the effectiveness of MMTS as it is able to achieve stability at every matching step, satisfies the incentive-compatibility property, and has a sublinear Bayesian regret over time. Our approach provides a useful method for addressing complementary preferences in real-world scenarios.

Graph Federated Learning with Hidden Representation Sharing

Learning on Graphs (LoG) is widely used in multi-client systems when each client has insufficient local data, and multiple clients have to share their raw data to learn a model of good quality. One scenario is to recommend items to clients with limited historical data and sharing similar preferences with other clients in a social network. On the other hand, due to the increasing demands for the protection of clients' data privacy, Federated Learning (FL) has been widely adopted: FL requires models to be trained in a multi-client system and restricts sharing of raw data among clients. The underlying potential data-sharing conflict between LoG and FL is under-explored and how to benefit from both sides is a promising problem. In this work, we first formulate the Graph Federated Learning (GFL) problem that unifies LoG and FL in multi-client systems and then propose sharing hidden representation instead of the raw data of neighbors to protect data privacy as a solution. To overcome the biased gradient problem in GFL, we provide a gradient estimation method and its convergence analysis under the non-convex objective. In experiments, we evaluate our method in classification tasks on graphs. Our experiment shows a good match between our theory and the practice.

Debiasing Neural Retrieval via In-batch Balancing Regularization

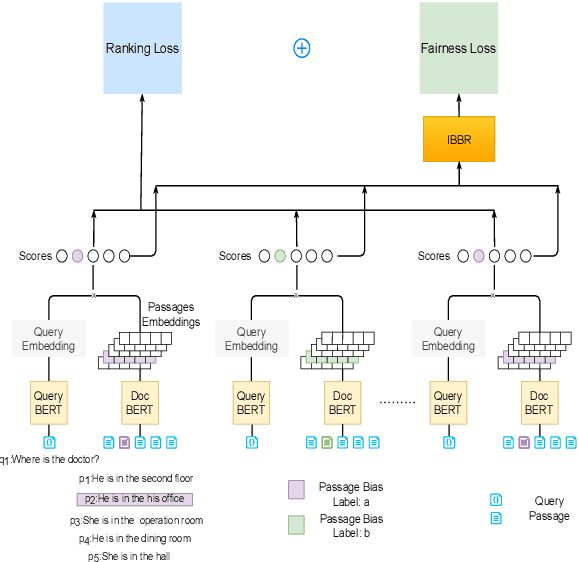
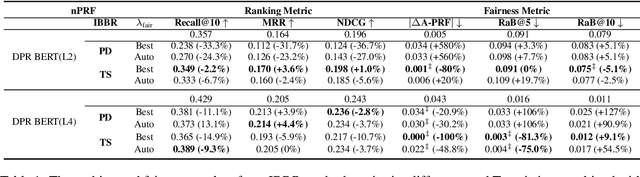
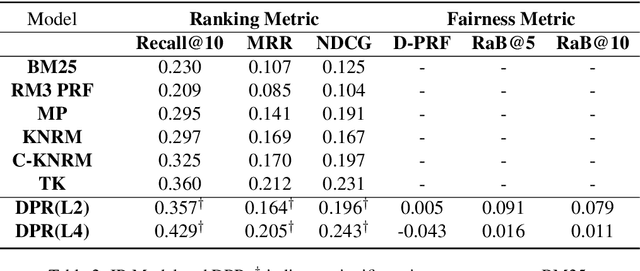
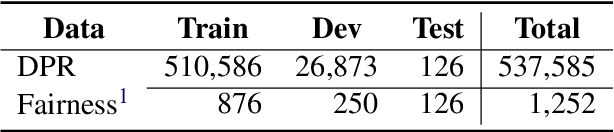
People frequently interact with information retrieval (IR) systems, however, IR models exhibit biases and discrimination towards various demographics. The in-processing fair ranking methods provide a trade-offs between accuracy and fairness through adding a fairness-related regularization term in the loss function. However, there haven't been intuitive objective functions that depend on the click probability and user engagement to directly optimize towards this. In this work, we propose the In-Batch Balancing Regularization (IBBR) to mitigate the ranking disparity among subgroups. In particular, we develop a differentiable \textit{normed Pairwise Ranking Fairness} (nPRF) and leverage the T-statistics on top of nPRF over subgroups as a regularization to improve fairness. Empirical results with the BERT-based neural rankers on the MS MARCO Passage Retrieval dataset with the human-annotated non-gendered queries benchmark \citep{rekabsaz2020neural} show that our IBBR method with nPRF achieves significantly less bias with minimal degradation in ranking performance compared with the baseline.

Rate-Optimal Contextual Online Matching Bandit

Two-sided online matching platforms have been employed in various markets. However, agents' preferences in present market are usually implicit and unknown and must be learned from data. With the growing availability of side information involved in the decision process, modern online matching methodology demands the capability to track preference dynamics for agents based on their contextual information. This motivates us to consider a novel Contextual Online Matching Bandit prOblem (COMBO), which allows dynamic preferences in matching decisions. Existing works focus on multi-armed bandit with static preference, but this is insufficient: the two-sided preference changes as along as one-side's contextual information updates, resulting in non-static matching. In this paper, we propose a Centralized Contextual - Explore Then Commit (CC-ETC) algorithm to adapt to the COMBO. CC-ETC solves online matching with dynamic preference. In theory, we show that CC-ETC achieves a sublinear regret upper bound O(log(T)) and is a rate-optimal algorithm by proving a matching lower bound. In the experiments, we demonstrate that CC-ETC is robust to variant preference schemes, dimensions of contexts, reward noise levels, and contexts variation levels.

Residual Bootstrap Exploration for Stochastic Linear Bandit

We propose a new bootstrap-based online algorithm for stochastic linear bandit problems. The key idea is to adopt residual bootstrap exploration, in which the agent estimates the next step reward by re-sampling the residuals of mean reward estimate. Our algorithm, residual bootstrap exploration for stochastic linear bandit (\texttt{LinReBoot}), estimates the linear reward from its re-sampling distribution and pulls the arm with the highest reward estimate. In particular, we contribute a theoretical framework to demystify residual bootstrap-based exploration mechanisms in stochastic linear bandit problems. The key insight is that the strength of bootstrap exploration is based on collaborated optimism between the online-learned model and the re-sampling distribution of residuals. Such observation enables us to show that the proposed \texttt{LinReBoot} secure a high-probability $\tilde{O}(d \sqrt{n})$ sub-linear regret under mild conditions. Our experiments support the easy generalizability of the \texttt{ReBoot} principle in the various formulations of linear bandit problems and show the significant computational efficiency of \texttt{LinReBoot}.

Online Bootstrap Inference For Policy Evaluation in Reinforcement Learning

The recent emergence of reinforcement learning has created a demand for robust statistical inference methods for the parameter estimates computed using these algorithms. Existing methods for statistical inference in online learning are restricted to settings involving independently sampled observations, while existing statistical inference methods in reinforcement learning (RL) are limited to the batch setting. The online bootstrap is a flexible and efficient approach for statistical inference in linear stochastic approximation algorithms, but its efficacy in settings involving Markov noise, such as RL, has yet to be explored. In this paper, we study the use of the online bootstrap method for statistical inference in RL. In particular, we focus on the temporal difference (TD) learning and Gradient TD (GTD) learning algorithms, which are themselves special instances of linear stochastic approximation under Markov noise. The method is shown to be distributionally consistent for statistical inference in policy evaluation, and numerical experiments are included to demonstrate the effectiveness of this algorithm at statistical inference tasks across a range of real RL environments.

Online Forgetting Process for Linear Regression Models

Motivated by the EU's "Right To Be Forgotten" regulation, we initiate a study of statistical data deletion problems where users' data are accessible only for a limited period of time. This setting is formulated as an online supervised learning task with \textit{constant memory limit}. We propose a deletion-aware algorithm \texttt{FIFD-OLS} for the low dimensional case, and witness a catastrophic rank swinging phenomenon due to the data deletion operation, which leads to statistical inefficiency. As a remedy, we propose the \texttt{FIFD-Adaptive Ridge} algorithm with a novel online regularization scheme, that effectively offsets the uncertainty from deletion. In theory, we provide the cumulative regret upper bound for both online forgetting algorithms. In the experiment, we showed \texttt{FIFD-Adaptive Ridge} outperforms the ridge regression algorithm with fixed regularization level, and hopefully sheds some light on more complex statistical models.

A Non-Iterative Quantile Change Detection Method in Mixture Model with Heavy-Tailed Components

Estimating parameters of mixture model has wide applications ranging from classification problems to estimating of complex distributions. Most of the current literature on estimating the parameters of the mixture densities are based on iterative Expectation Maximization (EM) type algorithms which require the use of either taking expectations over the latent label variables or generating samples from the conditional distribution of such latent labels using the Bayes rule. Moreover, when the number of components is unknown, the problem becomes computationally more demanding due to well-known label switching issues \cite{richardson1997bayesian}. In this paper, we propose a robust and quick approach based on change-point methods to determine the number of mixture components that works for almost any location-scale families even when the components are heavy tailed (e.g., Cauchy). We present several numerical illustrations by comparing our method with some of popular methods available in the literature using simulated data and real case studies. The proposed method is shown be as much as 500 times faster than some of the competing methods and are also shown to be more accurate in estimating the mixture distributions by goodness-of-fit tests.