E2N: Error Estimation Networks for Goal-Oriented Mesh Adaptation
Paper and Code
Jul 22, 2022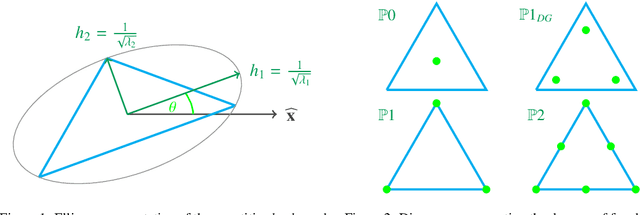
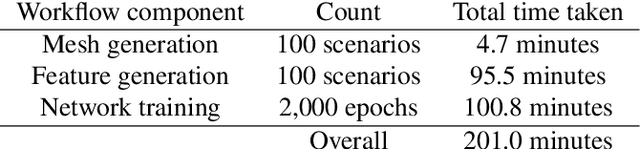


Given a partial differential equation (PDE), goal-oriented error estimation allows us to understand how errors in a diagnostic quantity of interest (QoI), or goal, occur and accumulate in a numerical approximation, for example using the finite element method. By decomposing the error estimates into contributions from individual elements, it is possible to formulate adaptation methods, which modify the mesh with the objective of minimising the resulting QoI error. However, the standard error estimate formulation involves the true adjoint solution, which is unknown in practice. As such, it is common practice to approximate it with an 'enriched' approximation (e.g. in a higher order space or on a refined mesh). Doing so generally results in a significant increase in computational cost, which can be a bottleneck compromising the competitiveness of (goal-oriented) adaptive simulations. The central idea of this paper is to develop a "data-driven" goal-oriented mesh adaptation approach through the selective replacement of the expensive error estimation step with an appropriately configured and trained neural network. In doing so, the error estimator may be obtained without even constructing the enriched spaces. An element-by-element construction is employed here, whereby local values of various parameters related to the mesh geometry and underlying problem physics are taken as inputs, and the corresponding contribution to the error estimator is taken as output. We demonstrate that this approach is able to obtain the same accuracy with a reduced computational cost, for adaptive mesh test cases related to flow around tidal turbines, which interact via their downstream wakes, and where the overall power output of the farm is taken as the QoI. Moreover, we demonstrate that the element-by-element approach implies reasonably low training costs.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge