Identification and estimation for matrix time series CP-factor models

We investigate the identification and the estimation for matrix time series CP-factor models. Unlike the generalized eigenanalysis-based method of Chang et al. (2023) which requires the two factor loading matrices to be full-ranked, the newly proposed estimation can handle rank-deficient factor loading matrices. The estimation procedure consists of the spectral decomposition of several matrices and a matrix joint diagonalization algorithm, resulting in low computational cost. The theoretical guarantee established without the stationarity assumption shows that the proposed estimation exhibits a faster convergence rate than that of Chang et al. (2023). In fact the new estimator is free from the adverse impact of any eigen-gaps, unlike most eigenanalysis-based methods such as that of Chang et al. (2023). Furthermore, in terms of the error rates of the estimation, the proposed procedure is equivalent to handling a vector time series of dimension $\max(p,q)$ instead of $p \times q$, where $(p, q)$ are the dimensions of the matrix time series concerned. We have achieved this without assuming the "near orthogonality" of the loadings under various incoherence conditions often imposed in the CP-decomposition literature, see Han and Zhang (2022), Han et al. (2024) and the references within. Illustration with both simulated and real matrix time series data shows the usefulness of the proposed approach.

Testing for the Markov Property in Time Series via Deep Conditional Generative Learning

The Markov property is widely imposed in analysis of time series data. Correspondingly, testing the Markov property, and relatedly, inferring the order of a Markov model, are of paramount importance. In this article, we propose a nonparametric test for the Markov property in high-dimensional time series via deep conditional generative learning. We also apply the test sequentially to determine the order of the Markov model. We show that the test controls the type-I error asymptotically, and has the power approaching one. Our proposal makes novel contributions in several ways. We utilize and extend state-of-the-art deep generative learning to estimate the conditional density functions, and establish a sharp upper bound on the approximation error of the estimators. We derive a doubly robust test statistic, which employs a nonparametric estimation but achieves a parametric convergence rate. We further adopt sample splitting and cross-fitting to minimize the conditions required to ensure the consistency of the test. We demonstrate the efficacy of the test through both simulations and the three data applications.

Modelling matrix time series via a tensor CP-decomposition

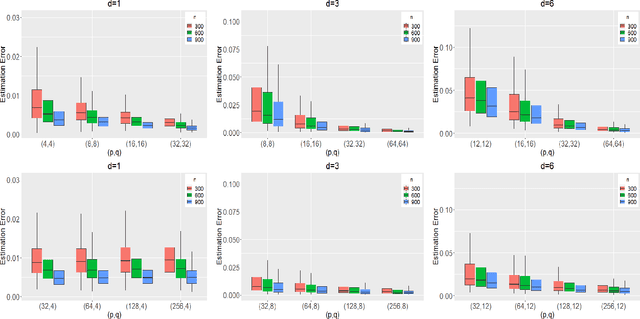
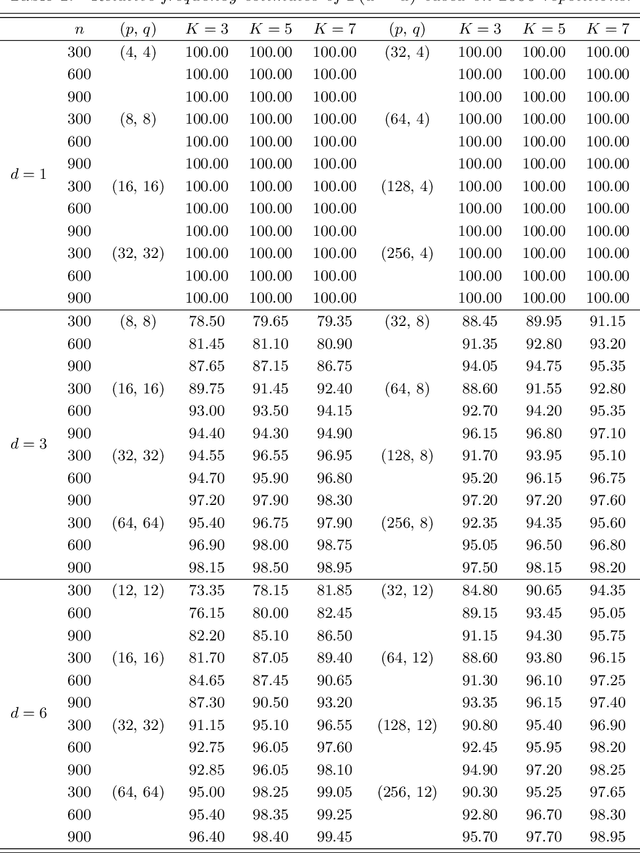
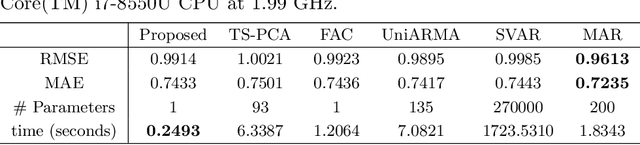
We propose to model matrix time series based on a tensor CP-decomposition. Instead of using an iterative algorithm which is the standard practice for estimating CP-decompositions, we propose a new and one-pass estimation procedure based on a generalized eigenanalysis constructed from the serial dependence structure of the underlying process. A key idea of the new procedure is to project a generalized eigenequation defined in terms of rank-reduced matrices to a lower-dimensional one with full-ranked matrices, to avoid the intricacy of the former of which the number of eigenvalues can be zero, finite and infinity. The asymptotic theory has been established under a general setting without the stationarity. It shows, for example, that all the component coefficient vectors in the CP-decomposition are estimated consistently with the different error rates, depending on the relative sizes between the dimensions of time series and the sample size. The proposed model and the estimation method are further illustrated with both simulated and real data; showing effective dimension-reduction in modelling and forecasting matrix time series.