Joint Learning of Unsupervised Multi-view Feature and Instance Co-selection with Cross-view Imputation

Feature and instance co-selection, which aims to reduce both feature dimensionality and sample size by identifying the most informative features and instances, has attracted considerable attention in recent years. However, when dealing with unlabeled incomplete multi-view data, where some samples are missing in certain views, existing methods typically first impute the missing data and then concatenate all views into a single dataset for subsequent co-selection. Such a strategy treats co-selection and missing data imputation as two independent processes, overlooking potential interactions between them. The inter-sample relationships gleaned from co-selection can aid imputation, which in turn enhances co-selection performance. Additionally, simply merging multi-view data fails to capture the complementary information among views, ultimately limiting co-selection effectiveness. To address these issues, we propose a novel co-selection method, termed Joint learning of Unsupervised multI-view feature and instance Co-selection with cross-viEw imputation (JUICE). JUICE first reconstructs incomplete multi-view data using available observations, bringing missing data recovery and feature and instance co-selection together in a unified framework. Then, JUICE leverages cross-view neighborhood information to learn inter-sample relationships and further refine the imputation of missing values during reconstruction. This enables the selection of more representative features and instances. Extensive experiments demonstrate that JUICE outperforms state-of-the-art methods.

Provable Diffusion Posterior Sampling for Bayesian Inversion

This paper proposes a novel diffusion-based posterior sampling method within a plug-and-play (PnP) framework. Our approach constructs a probability transport from an easy-to-sample terminal distribution to the target posterior, using a warm-start strategy to initialize the particles. To approximate the posterior score, we develop a Monte Carlo estimator in which particles are generated using Langevin dynamics, avoiding the heuristic approximations commonly used in prior work. The score governing the Langevin dynamics is learned from data, enabling the model to capture rich structural features of the underlying prior distribution. On the theoretical side, we provide non-asymptotic error bounds, showing that the method converges even for complex, multi-modal target posterior distributions. These bounds explicitly quantify the errors arising from posterior score estimation, the warm-start initialization, and the posterior sampling procedure. Our analysis further clarifies how the prior score-matching error and the condition number of the Bayesian inverse problem influence overall performance. Finally, we present numerical experiments demonstrating the effectiveness of the proposed method across a range of inverse problems.

Cross-view Joint Learning for Mixed-Missing Multi-view Unsupervised Feature Selection

Incomplete multi-view unsupervised feature selection (IMUFS), which aims to identify representative features from unlabeled multi-view data containing missing values, has received growing attention in recent years. Despite their promising performance, existing methods face three key challenges: 1) by focusing solely on the view-missing problem, they are not well-suited to the more prevalent mixed-missing scenario in practice, where some samples lack entire views or only partial features within views; 2) insufficient utilization of consistency and diversity across views limits the effectiveness of feature selection; and 3) the lack of theoretical analysis makes it unclear how feature selection and data imputation interact during the joint learning process. Being aware of these, we propose CLIM-FS, a novel IMUFS method designed to address the mixed-missing problem. Specifically, we integrate the imputation of both missing views and variables into a feature selection model based on nonnegative orthogonal matrix factorization, enabling the joint learning of feature selection and adaptive data imputation. Furthermore, we fully leverage consensus cluster structure and cross-view local geometrical structure to enhance the synergistic learning process. We also provide a theoretical analysis to clarify the underlying collaborative mechanism of CLIM-FS. Experimental results on eight real-world multi-view datasets demonstrate that CLIM-FS outperforms state-of-the-art methods.

Bayesian penalized empirical likelihood and MCMC sampling

In this study, we introduce a novel methodological framework called Bayesian Penalized Empirical Likelihood (BPEL), designed to address the computational challenges inherent in empirical likelihood (EL) approaches. Our approach has two primary objectives: (i) to enhance the inherent flexibility of EL in accommodating diverse model conditions, and (ii) to facilitate the use of well-established Markov Chain Monte Carlo (MCMC) sampling schemes as a convenient alternative to the complex optimization typically required for statistical inference using EL. To achieve the first objective, we propose a penalized approach that regularizes the Lagrange multipliers, significantly reducing the dimensionality of the problem while accommodating a comprehensive set of model conditions. For the second objective, our study designs and thoroughly investigates two popular sampling schemes within the BPEL context. We demonstrate that the BPEL framework is highly flexible and efficient, enhancing the adaptability and practicality of EL methods. Our study highlights the practical advantages of using sampling techniques over traditional optimization methods for EL problems, showing rapid convergence to the global optima of posterior distributions and ensuring the effective resolution of complex statistical inference challenges.

Identification and estimation for matrix time series CP-factor models

We investigate the identification and the estimation for matrix time series CP-factor models. Unlike the generalized eigenanalysis-based method of Chang et al. (2023) which requires the two factor loading matrices to be full-ranked, the newly proposed estimation can handle rank-deficient factor loading matrices. The estimation procedure consists of the spectral decomposition of several matrices and a matrix joint diagonalization algorithm, resulting in low computational cost. The theoretical guarantee established without the stationarity assumption shows that the proposed estimation exhibits a faster convergence rate than that of Chang et al. (2023). In fact the new estimator is free from the adverse impact of any eigen-gaps, unlike most eigenanalysis-based methods such as that of Chang et al. (2023). Furthermore, in terms of the error rates of the estimation, the proposed procedure is equivalent to handling a vector time series of dimension $\max(p,q)$ instead of $p \times q$, where $(p, q)$ are the dimensions of the matrix time series concerned. We have achieved this without assuming the "near orthogonality" of the loadings under various incoherence conditions often imposed in the CP-decomposition literature, see Han and Zhang (2022), Han et al. (2024) and the references within. Illustration with both simulated and real matrix time series data shows the usefulness of the proposed approach.

Deep Conditional Generative Learning: Model and Error Analysis

We introduce an Ordinary Differential Equation (ODE) based deep generative method for learning a conditional distribution, named the Conditional Follmer Flow. Starting from a standard Gaussian distribution, the proposed flow could efficiently transform it into the target conditional distribution at time 1. For effective implementation, we discretize the flow with Euler's method where we estimate the velocity field nonparametrically using a deep neural network. Furthermore, we derive a non-asymptotic convergence rate in the Wasserstein distance between the distribution of the learned samples and the target distribution, providing the first comprehensive end-to-end error analysis for conditional distribution learning via ODE flow. Our numerical experiments showcase its effectiveness across a range of scenarios, from standard nonparametric conditional density estimation problems to more intricate challenges involving image data, illustrating its superiority over various existing conditional density estimation methods.

Efficiently handling constraints with Metropolis-adjusted Langevin algorithm

In this study, we investigate the performance of the Metropolis-adjusted Langevin algorithm in a setting with constraints on the support of the target distribution. We provide a rigorous analysis of the resulting Markov chain, establishing its convergence and deriving an upper bound for its mixing time. Our results demonstrate that the Metropolis-adjusted Langevin algorithm is highly effective in handling this challenging situation: the mixing time bound we obtain is superior to the best known bounds for competing algorithms without an accept-reject step. Our numerical experiments support these theoretical findings, indicating that the Metropolis-adjusted Langevin algorithm shows promising performance when dealing with constraints on the support of the target distribution.

Modelling matrix time series via a tensor CP-decomposition

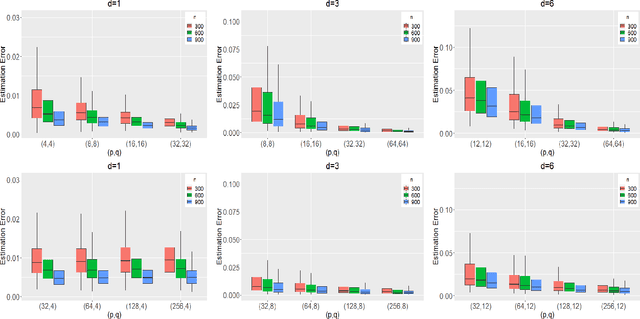
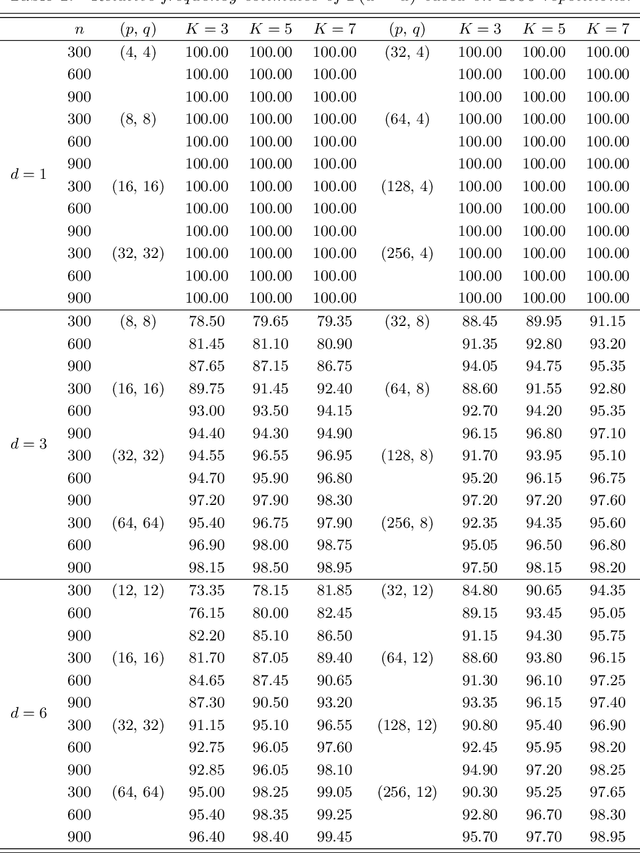
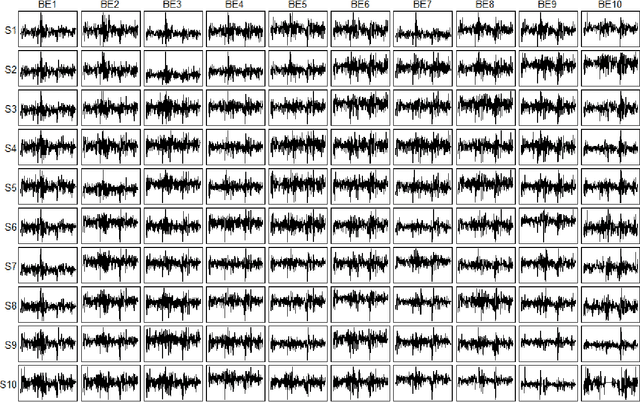
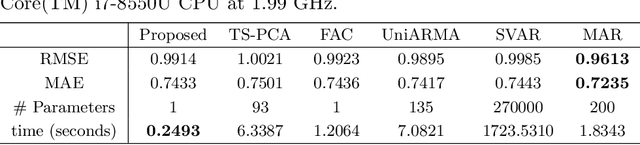
We propose to model matrix time series based on a tensor CP-decomposition. Instead of using an iterative algorithm which is the standard practice for estimating CP-decompositions, we propose a new and one-pass estimation procedure based on a generalized eigenanalysis constructed from the serial dependence structure of the underlying process. A key idea of the new procedure is to project a generalized eigenequation defined in terms of rank-reduced matrices to a lower-dimensional one with full-ranked matrices, to avoid the intricacy of the former of which the number of eigenvalues can be zero, finite and infinity. The asymptotic theory has been established under a general setting without the stationarity. It shows, for example, that all the component coefficient vectors in the CP-decomposition are estimated consistently with the different error rates, depending on the relative sizes between the dimensions of time series and the sample size. The proposed model and the estimation method are further illustrated with both simulated and real data; showing effective dimension-reduction in modelling and forecasting matrix time series.