Bayesian penalized empirical likelihood and MCMC sampling

In this study, we introduce a novel methodological framework called Bayesian Penalized Empirical Likelihood (BPEL), designed to address the computational challenges inherent in empirical likelihood (EL) approaches. Our approach has two primary objectives: (i) to enhance the inherent flexibility of EL in accommodating diverse model conditions, and (ii) to facilitate the use of well-established Markov Chain Monte Carlo (MCMC) sampling schemes as a convenient alternative to the complex optimization typically required for statistical inference using EL. To achieve the first objective, we propose a penalized approach that regularizes the Lagrange multipliers, significantly reducing the dimensionality of the problem while accommodating a comprehensive set of model conditions. For the second objective, our study designs and thoroughly investigates two popular sampling schemes within the BPEL context. We demonstrate that the BPEL framework is highly flexible and efficient, enhancing the adaptability and practicality of EL methods. Our study highlights the practical advantages of using sampling techniques over traditional optimization methods for EL problems, showing rapid convergence to the global optima of posterior distributions and ensuring the effective resolution of complex statistical inference challenges.

Efficiently handling constraints with Metropolis-adjusted Langevin algorithm

In this study, we investigate the performance of the Metropolis-adjusted Langevin algorithm in a setting with constraints on the support of the target distribution. We provide a rigorous analysis of the resulting Markov chain, establishing its convergence and deriving an upper bound for its mixing time. Our results demonstrate that the Metropolis-adjusted Langevin algorithm is highly effective in handling this challenging situation: the mixing time bound we obtain is superior to the best known bounds for competing algorithms without an accept-reject step. Our numerical experiments support these theoretical findings, indicating that the Metropolis-adjusted Langevin algorithm shows promising performance when dealing with constraints on the support of the target distribution.

Homotopic Gradients of Generative Density Priors for MR Image Reconstruction

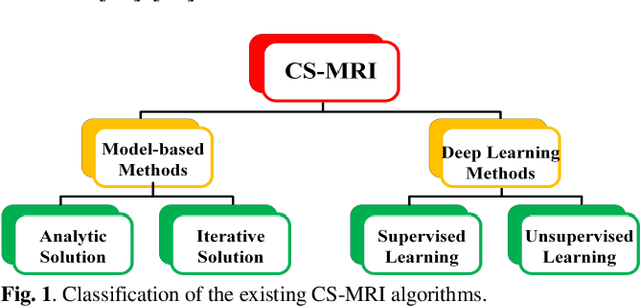
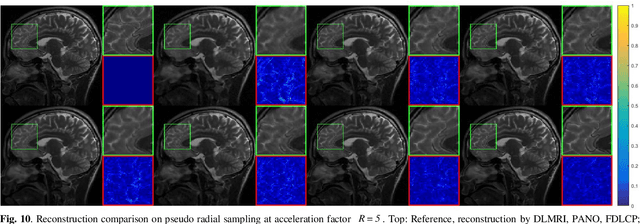
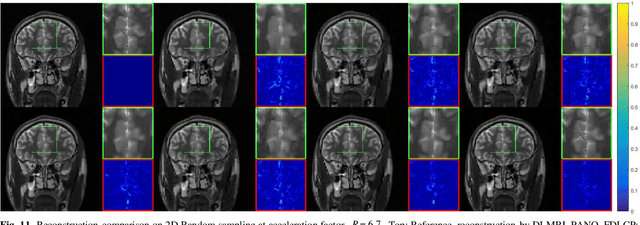
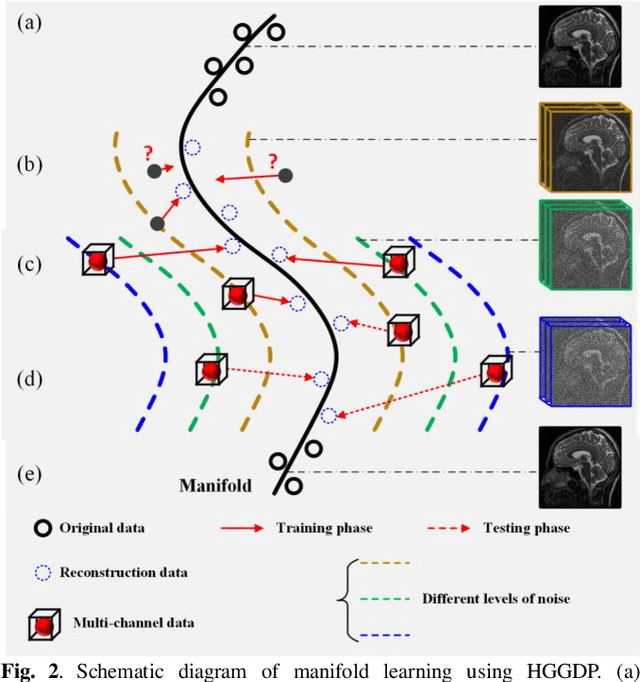
Deep learning, particularly the generative model, has demonstrated tremendous potential to significantly speed up image reconstruction with reduced measurements recently. Rather than the existing generative models that often optimize the density priors, in this work, by taking advantage of the denoising score matching, homotopic gradients of generative density priors (HGGDP) are proposed for magnetic resonance imaging (MRI) reconstruction. More precisely, to tackle the low-dimensional manifold and low data density region issues in generative density prior, we estimate the target gradients in higher-dimensional space. We train a more powerful noise conditional score network by forming high-dimensional tensor as the network input at the training phase. More artificial noise is also injected in the embedding space. At the reconstruction stage, a homotopy method is employed to pursue the density prior, such as to boost the reconstruction performance. Experiment results imply the remarkable performance of HGGDP in terms of high reconstruction accuracy; only 10% of the k-space data can still generate images of high quality as effectively as standard MRI reconstruction with the fully sampled data.