Jinjie Zhou
Homotopic Gradients of Generative Density Priors for MR Image Reconstruction
Aug 14, 2020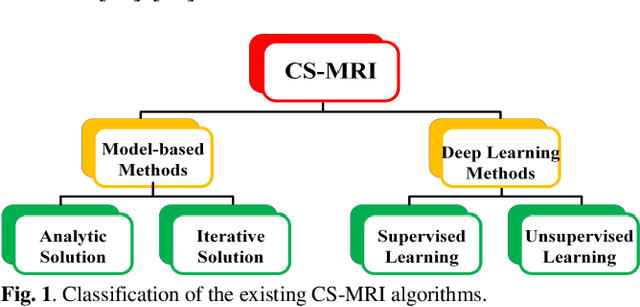
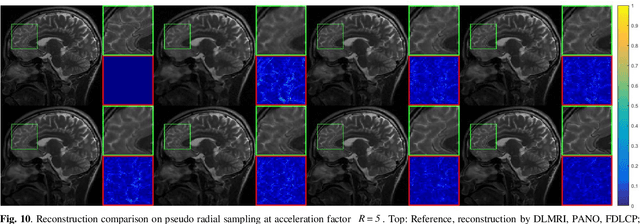
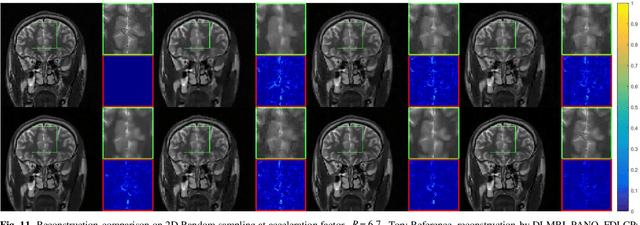
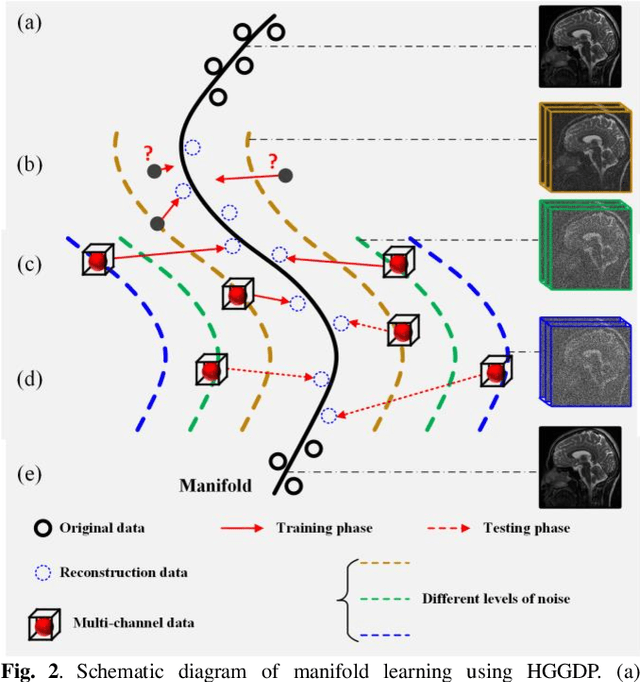
Abstract:Deep learning, particularly the generative model, has demonstrated tremendous potential to significantly speed up image reconstruction with reduced measurements recently. Rather than the existing generative models that often optimize the density priors, in this work, by taking advantage of the denoising score matching, homotopic gradients of generative density priors (HGGDP) are proposed for magnetic resonance imaging (MRI) reconstruction. More precisely, to tackle the low-dimensional manifold and low data density region issues in generative density prior, we estimate the target gradients in higher-dimensional space. We train a more powerful noise conditional score network by forming high-dimensional tensor as the network input at the training phase. More artificial noise is also injected in the embedding space. At the reconstruction stage, a homotopy method is employed to pursue the density prior, such as to boost the reconstruction performance. Experiment results imply the remarkable performance of HGGDP in terms of high reconstruction accuracy; only 10% of the k-space data can still generate images of high quality as effectively as standard MRI reconstruction with the fully sampled data.
Learning Priors in High-frequency Domain for Inverse Imaging Reconstruction
Oct 23, 2019



Abstract:Ill-posed inverse problems in imaging remain an active research topic in several decades, with new approaches constantly emerging. Recognizing that the popular dictionary learning and convolutional sparse coding are both essentially modeling the high-frequency component of an image, which convey most of the semantic information such as texture details, in this work we propose a novel multi-profile high-frequency transform-guided denoising autoencoder as prior (HF-DAEP). To achieve this goal, we first extract a set of multi-profile high-frequency components via a specific transformation and add the artificial Gaussian noise to these high-frequency components as training samples. Then, as the high-frequency prior information is learned, we incorporate it into classical iterative reconstruction process by proximal gradient descent technique. Preliminary results on highly under-sampled magnetic resonance imaging and sparse-view computed tomography reconstruction demonstrate that the proposed method can efficiently reconstruct feature details and present advantages over state-of-the-arts.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge