Bayesian penalized empirical likelihood and MCMC sampling

In this study, we introduce a novel methodological framework called Bayesian Penalized Empirical Likelihood (BPEL), designed to address the computational challenges inherent in empirical likelihood (EL) approaches. Our approach has two primary objectives: (i) to enhance the inherent flexibility of EL in accommodating diverse model conditions, and (ii) to facilitate the use of well-established Markov Chain Monte Carlo (MCMC) sampling schemes as a convenient alternative to the complex optimization typically required for statistical inference using EL. To achieve the first objective, we propose a penalized approach that regularizes the Lagrange multipliers, significantly reducing the dimensionality of the problem while accommodating a comprehensive set of model conditions. For the second objective, our study designs and thoroughly investigates two popular sampling schemes within the BPEL context. We demonstrate that the BPEL framework is highly flexible and efficient, enhancing the adaptability and practicality of EL methods. Our study highlights the practical advantages of using sampling techniques over traditional optimization methods for EL problems, showing rapid convergence to the global optima of posterior distributions and ensuring the effective resolution of complex statistical inference challenges.

Efficiently handling constraints with Metropolis-adjusted Langevin algorithm

In this study, we investigate the performance of the Metropolis-adjusted Langevin algorithm in a setting with constraints on the support of the target distribution. We provide a rigorous analysis of the resulting Markov chain, establishing its convergence and deriving an upper bound for its mixing time. Our results demonstrate that the Metropolis-adjusted Langevin algorithm is highly effective in handling this challenging situation: the mixing time bound we obtain is superior to the best known bounds for competing algorithms without an accept-reject step. Our numerical experiments support these theoretical findings, indicating that the Metropolis-adjusted Langevin algorithm shows promising performance when dealing with constraints on the support of the target distribution.

Pre-processing with Orthogonal Decompositions for High-dimensional Explanatory Variables

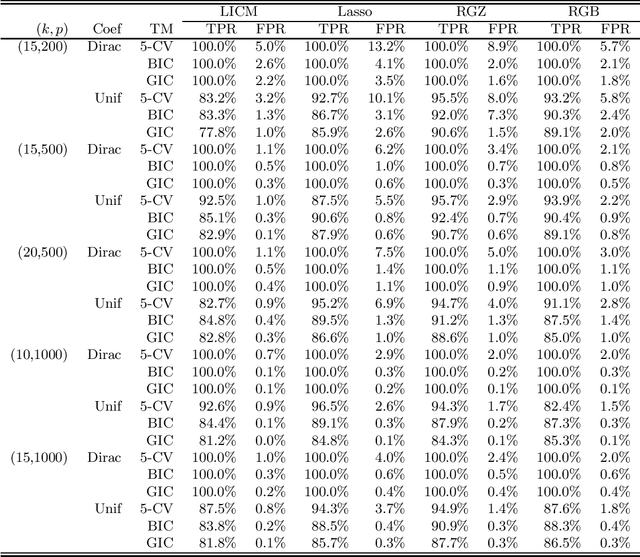
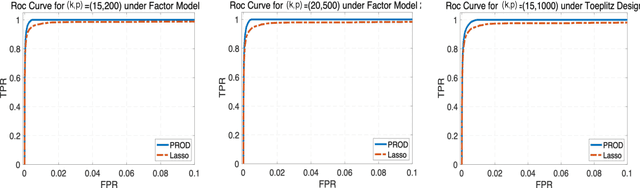
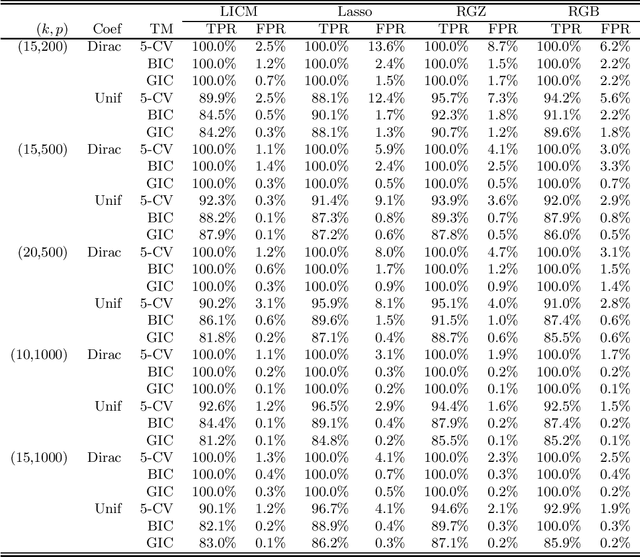
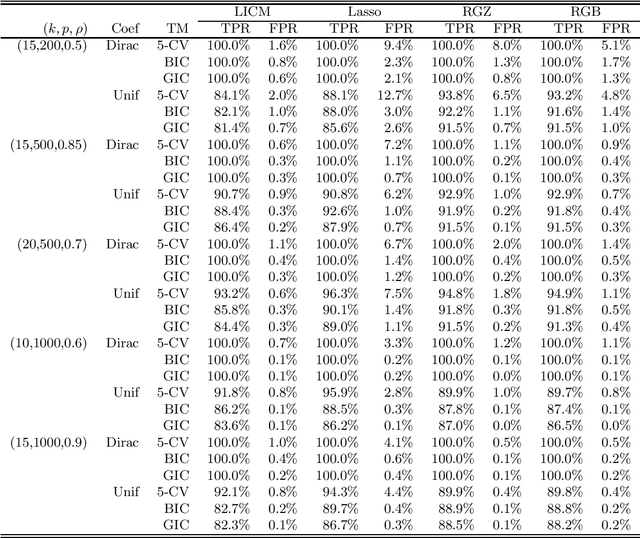
Strong correlations between explanatory variables are problematic for high-dimensional regularized regression methods. Due to the violation of the Irrepresentable Condition, the popular LASSO method may suffer from false inclusions of inactive variables. In this paper, we propose pre-processing with orthogonal decompositions (PROD) for the explanatory variables in high-dimensional regressions. The PROD procedure is constructed based upon a generic orthogonal decomposition of the design matrix. We demonstrate by two concrete cases that the PROD approach can be effectively constructed for improving the performance of high-dimensional penalized regression. Our theoretical analysis reveals their properties and benefits for high-dimensional penalized linear regression with LASSO. Extensive numerical studies with simulations and data analysis show the promising performance of the PROD.

Tuning parameter selection in high dimensional penalized likelihood

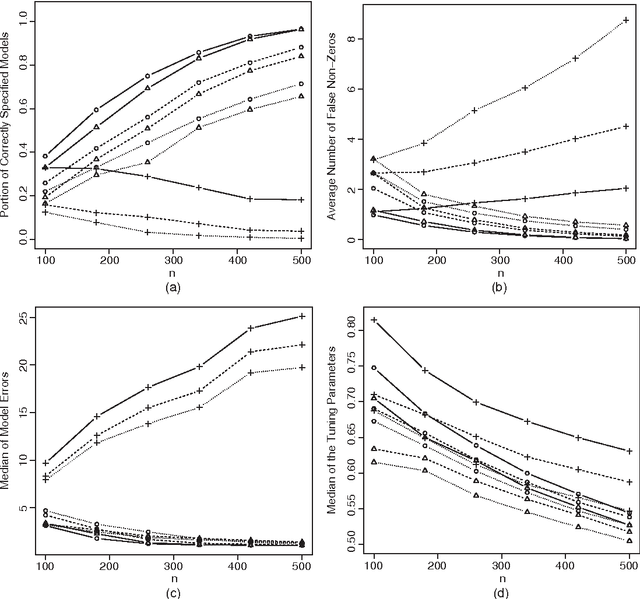
Determining how to appropriately select the tuning parameter is essential in penalized likelihood methods for high-dimensional data analysis. We examine this problem in the setting of penalized likelihood methods for generalized linear models, where the dimensionality of covariates p is allowed to increase exponentially with the sample size n. We propose to select the tuning parameter by optimizing the generalized information criterion (GIC) with an appropriate model complexity penalty. To ensure that we consistently identify the true model, a range for the model complexity penalty is identified in GIC. We find that this model complexity penalty should diverge at the rate of some power of $\log p$ depending on the tail probability behavior of the response variables. This reveals that using the AIC or BIC to select the tuning parameter may not be adequate for consistently identifying the true model. Based on our theoretical study, we propose a uniform choice of the model complexity penalty and show that the proposed approach consistently identifies the true model among candidate models with asymptotic probability one. We justify the performance of the proposed procedure by numerical simulations and a gene expression data analysis.