Provable Diffusion Posterior Sampling for Bayesian Inversion

This paper proposes a novel diffusion-based posterior sampling method within a plug-and-play (PnP) framework. Our approach constructs a probability transport from an easy-to-sample terminal distribution to the target posterior, using a warm-start strategy to initialize the particles. To approximate the posterior score, we develop a Monte Carlo estimator in which particles are generated using Langevin dynamics, avoiding the heuristic approximations commonly used in prior work. The score governing the Langevin dynamics is learned from data, enabling the model to capture rich structural features of the underlying prior distribution. On the theoretical side, we provide non-asymptotic error bounds, showing that the method converges even for complex, multi-modal target posterior distributions. These bounds explicitly quantify the errors arising from posterior score estimation, the warm-start initialization, and the posterior sampling procedure. Our analysis further clarifies how the prior score-matching error and the condition number of the Bayesian inverse problem influence overall performance. Finally, we present numerical experiments demonstrating the effectiveness of the proposed method across a range of inverse problems.

DRM Revisited: A Complete Error Analysis

In this work, we address a foundational question in the theoretical analysis of the Deep Ritz Method (DRM) under the over-parameteriztion regime: Given a target precision level, how can one determine the appropriate number of training samples, the key architectural parameters of the neural networks, the step size for the projected gradient descent optimization procedure, and the requisite number of iterations, such that the output of the gradient descent process closely approximates the true solution of the underlying partial differential equation to the specified precision?

Characteristic Learning for Provable One Step Generation

We propose the characteristic generator, a novel one-step generative model that combines the efficiency of sampling in Generative Adversarial Networks (GANs) with the stable performance of flow-based models. Our model is driven by characteristics, along which the probability density transport can be described by ordinary differential equations (ODEs). Specifically, We estimate the velocity field through nonparametric regression and utilize Euler method to solve the probability flow ODE, generating a series of discrete approximations to the characteristics. We then use a deep neural network to fit these characteristics, ensuring a one-step mapping that effectively pushes the prior distribution towards the target distribution. In the theoretical aspect, we analyze the errors in velocity matching, Euler discretization, and characteristic fitting to establish a non-asymptotic convergence rate for the characteristic generator in 2-Wasserstein distance. To the best of our knowledge, this is the first thorough analysis for simulation-free one step generative models. Additionally, our analysis refines the error analysis of flow-based generative models in prior works. We apply our method on both synthetic and real datasets, and the results demonstrate that the characteristic generator achieves high generation quality with just a single evaluation of neural network.

The Solution for the CVPR2024 NICE Image Captioning Challenge

This report introduces a solution to the Topic 1 Zero-shot Image Captioning of 2024 NICE : New frontiers for zero-shot Image Captioning Evaluation. In contrast to NICE 2023 datasets, this challenge involves new annotations by humans with significant differences in caption style and content. Therefore, we enhance image captions effectively through retrieval augmentation and caption grading methods. At the data level, we utilize high-quality captions generated by image caption models as training data to address the gap in text styles. At the model level, we employ OFA (a large-scale visual-language pre-training model based on handcrafted templates) to perform the image captioning task. Subsequently, we propose caption-level strategy for the high-quality caption data generated by the image caption models and integrate them with retrieval augmentation strategy into the template to compel the model to generate higher quality, more matching, and semantically enriched captions based on the retrieval augmentation prompts. Our approach ranks first on the leaderboard, achieving a CIDEr score of 234.11 and 1st in all other metrics.

Deep Conditional Generative Learning: Model and Error Analysis

We introduce an Ordinary Differential Equation (ODE) based deep generative method for learning a conditional distribution, named the Conditional Follmer Flow. Starting from a standard Gaussian distribution, the proposed flow could efficiently transform it into the target conditional distribution at time 1. For effective implementation, we discretize the flow with Euler's method where we estimate the velocity field nonparametrically using a deep neural network. Furthermore, we derive a non-asymptotic convergence rate in the Wasserstein distance between the distribution of the learned samples and the target distribution, providing the first comprehensive end-to-end error analysis for conditional distribution learning via ODE flow. Our numerical experiments showcase its effectiveness across a range of scenarios, from standard nonparametric conditional density estimation problems to more intricate challenges involving image data, illustrating its superiority over various existing conditional density estimation methods.

Inpaint4DNeRF: Promptable Spatio-Temporal NeRF Inpainting with Generative Diffusion Models

Current Neural Radiance Fields (NeRF) can generate photorealistic novel views. For editing 3D scenes represented by NeRF, with the advent of generative models, this paper proposes Inpaint4DNeRF to capitalize on state-of-the-art stable diffusion models (e.g., ControlNet) for direct generation of the underlying completed background content, regardless of static or dynamic. The key advantages of this generative approach for NeRF inpainting are twofold. First, after rough mask propagation, to complete or fill in previously occluded content, we can individually generate a small subset of completed images with plausible content, called seed images, from which simple 3D geometry proxies can be derived. Second and the remaining problem is thus 3D multiview consistency among all completed images, now guided by the seed images and their 3D proxies. Without other bells and whistles, our generative Inpaint4DNeRF baseline framework is general which can be readily extended to 4D dynamic NeRFs, where temporal consistency can be naturally handled in a similar way as our multiview consistency.

Registering Neural Radiance Fields as 3D Density Images

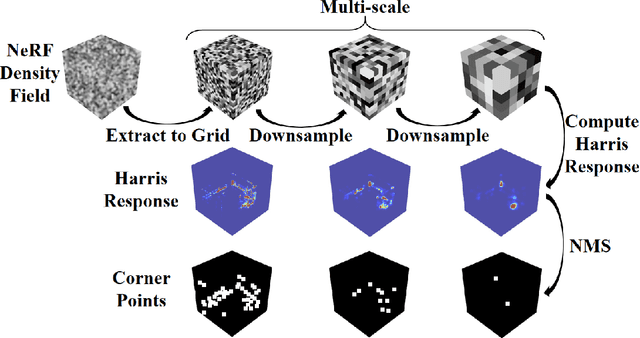
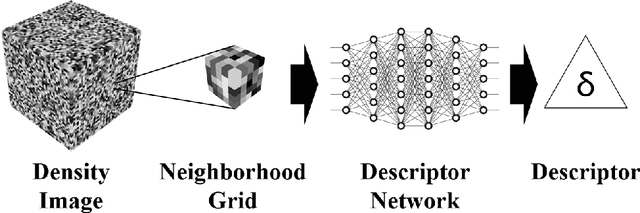
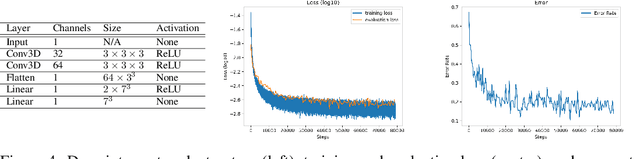
No significant work has been done to directly merge two partially overlapping scenes using NeRF representations. Given pre-trained NeRF models of a 3D scene with partial overlapping, this paper aligns them with a rigid transform, by generalizing the traditional registration pipeline, that is, key point detection and point set registration, to operate on 3D density fields. To describe corner points as key points in 3D, we propose to use universal pre-trained descriptor-generating neural networks that can be trained and tested on different scenes. We perform experiments to demonstrate that the descriptor networks can be conveniently trained using a contrastive learning strategy. We demonstrate that our method, as a global approach, can effectively register NeRF models, thus making possible future large-scale NeRF construction by registering its smaller and overlapping NeRFs captured individually.